1.7. Тригонометрическая форма комплексного числа

Определение. Совокупность, состоящая из точки О, оси ОР и единичного направленного отрезка ОЕ, образует систему координат на плоскости, которую будем называть полярной системой координат.

Т очку О называют полюсом, ОР – полярной осью, r – полярным радиусом точки M,  - угол между векторами OM и OP - полярным углом точки M (Рис. 3).

Рис. 3

0  

0 <2

Определение. Модулем комплексного числа будем называть неотрицательное действительное число z=a+bi= = .

Рассмотрим треугольник AOZ (Рис. 4). Из теоремы Пифагора очевидно, что полярный радиус точки Z совпадает с модулем соответствующего комплексного числа: r=|z|= .

Рис. 4

Определение. Координатную плоскость, служащую для изображения комплексного числа, будем называть комплексной плоскостью.

Определение. Аргументом комплексного числа называется угол , который образует вектор OZ с положительным направлением оси абсцисс (т.е. полярный угол точки Z): =argz.

Справедливы следующие соотношения:

,

,

,

,

Если в запись комплексного числа z вместо a и b подставить указанные выше значения, то получим

z=a+bi=rcos+irsin=r(cos+isin).

Таким образом, мы получили новую форму записи комплексного числа:

z=r(cos+isin),

которая называется тригонометрической формой комплексного числа.

Пример.

I. Записать в тригонометрической форме комплексное число z=1+i.

Решение.

1) Так как a=1, b=1, то

2) Изобразим число z геометрически (Рис. 5). Мы видим, что числу z соответствует точка Z, лежащая в I четверти, и вектор z.

3) Составим соотношения и , т.е.

,

Рис. 5

Этим соотношениям соответствует в I четверти угол 45.

4) Так как ,

то тригонометрическая форма заданного комплексного числа имеет вид

.

II. Записать число в тригонометрической форме.

Решение.

1) Здесь a=-2, .

Следовательно, .

2) Изобразим число z геометрически (Рис. 6). Мы видим, что числу z соответствует точка Z, лежащая во II четверти, и вектор z.

3) Находим

,

Этим соотношениям соответствует угол =180°-60°=120° .

4) Запишем заданное число в тригонометрической форме:

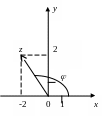
Рис. 6

III. Записать в тригонометрической форме чисто мнимое число z=-3i.

Решение.

1) Запишем данное число в виде z=0-3i. Значит, a=0, b=-3, откуда

2) Точка, соответствующая геометрически числу z=-3i, лежит на мнимой оси (Рис. 7).

3) Аргумент этого числа равен , так как угол отсчитывается от положительного направления оси Ox против часовой стрелки.

4) Запишем данное число в тригонометрической форме:

Рис. 7

1.8. Действия над комплексными числами в тригонометрической форме

Рассмотрим два комплексных числа, записанные в тригонометрической форме:

z₁=r₁(cos₁+isin₁)

z₂=r₂(cos₂+isin₂).

Очевидно следующее

Утверждение. z₁=z₂ тогда и только тогда, когда r₁=r₂, ₁=₂+2k, kZ.

Непосредственной проверкой легко убедиться в справедливости следующих теорем.

Теорема. При умножении двух комплексных чисел их модули умножаются, а аргументы складываются:

r₁(cos₁+isin₁)r₂(cos₂+isin₂)=r₁r₂[cos(₁+₂)+isin(₁+₂)]

Теорема. При делении комплексных чисел их модули делятся, а аргументы вычитаются:

Замечание. Если r₂=0, т.е. z₂=0, то деление невозможно.