4.3. Разложение определителя по строке (столбцу)

Определение. Минором элемента квадратной матрицы A называется определитель матрицы, полученной из матрицы A вычеркиванием i-ой строки и k-ого столбца. Обозначение: .

Выражение вида: , будем называть алгебраическим дополнением элемента матрицы A.

Теорема. Определитель матрицы A n-ого порядка равен сумме произведений элементов произвольной строки (столбца) на соответствующие алгебраические дополнения:

- разложение по строке;

- разложение по столбцу.

Доказательство.

Воспользуемся свойствами 5, 2 и определением определителей:

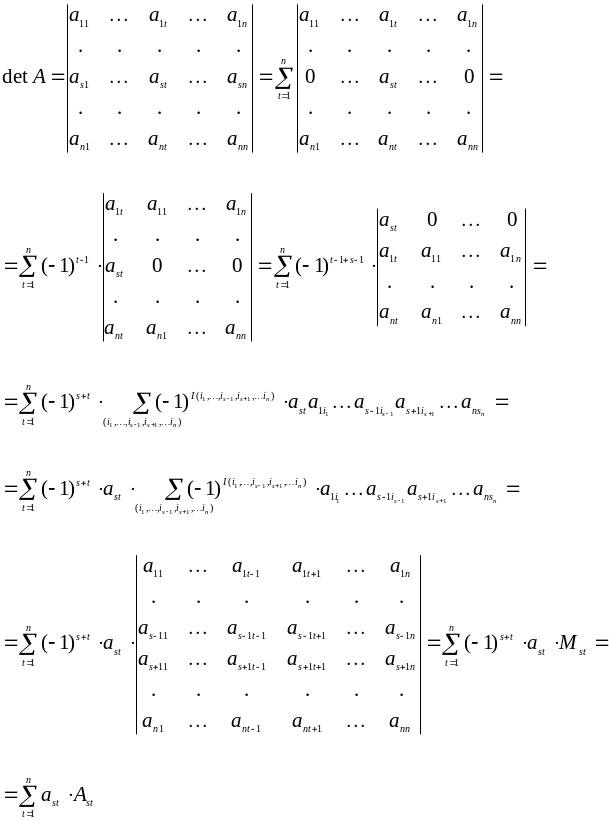
Формула разложения по столбцу доказывается аналогично.

Пример.

Вычислим определитель разложением по 1-й строке:

Теорема. Сумма произведений элементов какой-либо строки (столбца) на алгебраические дополнения элементов другой строки (столбца) равна 0, т.е. справедлива формула:

(здесь - символ Кронекера).

Доказательство.

При i=j утверждение совпадает с предыдущей теоремой. Остается рассмотреть случай ij. Введем матрицу A, получающуюся из A заменой j-й строки на i-ю:

.

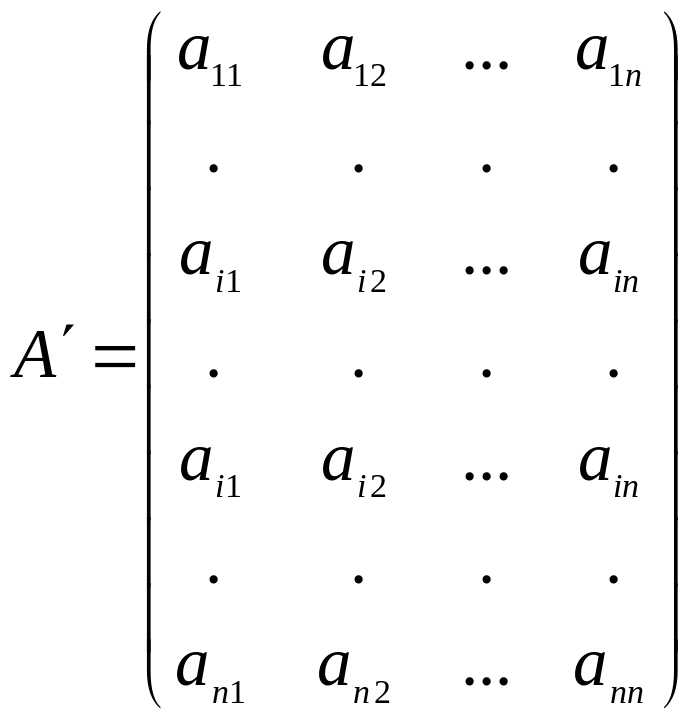Согласно свойству 3 определителей, будет . С другой стороны, раскладывая, в соответствии с предыдущей теоремой, определитель A по j-й строке, имеем: . Сравнивая правые части, получаем искомое. Теорема доказана.

4.4. Применение определителей. Правило Крамера

Теорема Крамера. Пусть задана система линейных уравнений, содержащая n уравнений и n неизвестных:

(*)

Тогда, если определитель основной матрицы системы отличен от 0, система имеет единственное решение:

(**),

где

- основная матрица системы, =detA, (k-ый столбец матрицы A заменен столбцом свободных членов).

Доказательство.

Докажем сначала единственность решения. Домножим i-е уравнение системы на алгебраическое дополнение A_ik и просуммируем получившиеся уравнения:

.

Перегруппировав слагаемые и вынося за скобки x_i: ,

Но - разложение определителя по столбцу.

,

По теореме из предыдущего раздела:

.

Получаем: , .

Поскольку по предположению 0, то . Ввиду произвольности k получаем: .

Таким образом, если вектор служит решением системы (*), его координаты удовлетворяют формулам (**).

Обратно, пусть координаты вектора получены по формулам (**). Умножая матрицу A справа на столбец 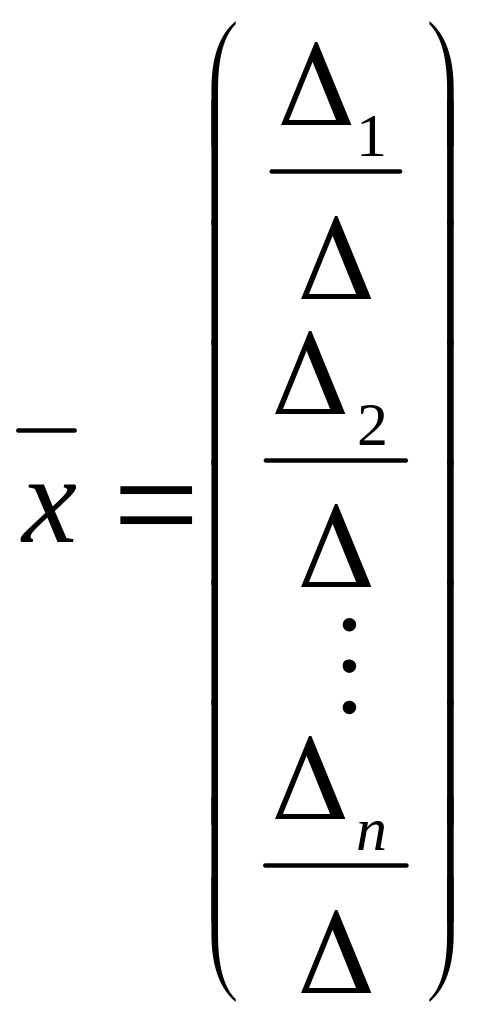, получаем вектор-столбец S, k-я координата которого равна

т.е. столбец .

Таким образом, вектор-столбец служит решением матричного уравнения . А это равносильно (см. пункт 3.3.) тому, что - решение системы (*). Теорема доказана.

4.5. Вычисление обратной матрицы

Теорема. Пусть A – неособенная матрица, т.е. =detA≠0. Тогда существует матрица - обратная к A, причем , где (матрица из алгебраических дополнений к элементам A, транспонированная).

Доказательство.

Достаточно проверить выполнение равенства . Но

,

т.к.

.

Теорема доказана.