Вариант № 40
1. Решить систему уравнений по правилу Крамера, методом Гаусса
и матричным методом
2. Выполнить действия над матрицами
3. Даны вершины треугольника АВС :
А(1; -4; 0) , В(0;2; 1) , С(-1; -2; 3) .
Найти : а) угол АВС ,
б) площадь треугольника АВС .
4. Задана пирамида с вершинами А1(-1; 3; 0), А2(2; 0; 0), А3(4; -1; 2),
А4(3; 2; 7). Найти объем пирамиды.
5. Даны вершины треугольника А (-2;5) , В (0;4) , С (1;6). Найти угол между сторонами АВ и ВС .
6. Даны координаты вершин пирамиды: А (1;1;-2), В (-2;2;1), С (1;-2;-3),
D (4;-1;1). Найти угол между гранями АВС и АВD .
7. Найти фокусы, полуоси, эксцентриситет кривой второго порядка. Сделать рисунок
.
8. Составить уравнение параболы, которая имеет фокус и проходит через начало координат. Сделать рисунок.
Пример выполнения задания
1. Решить систему уравнений по правилу Крамера, методом Гаусса и матричным методом
.
□
а) Правило Крамера:
.
,
значит система имеет един-ственное
решение.
,
т.е.
б)
Метод Гаусса :
.
,
,
.
Следоватедьно, .
в) Матричный метод :
.
А Х В
,
где
обратная матрица.
.
.
Следовательно, обратная матрица
существует.
т.е.
.
■
2. Выполнить действия над матрицами
□
.
■
3. Даны вершины треугольника АВС :
А(2; 3; 2) , В(3; -1; -2) , С(4; 3; -1) .
Найти : а) угол АВС ,
б) площадь треугольника АВС .
□
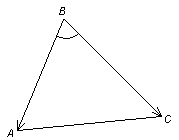
а) угол АВС :
.
Воспользуемся формулой определения угла между векторами:
б) площадь треугольника АВС :
Площадь треугольника можно определить по формуле:
■
4. Задана пирамида с вершинами А1(1; -2; 1), А2(0; 0; 4), А3(1; 4; 2),
А4(2; 0; 0). Найти объем пирамиды.
□
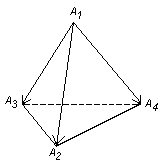
Объем пирамиды можно определить по фомуле:
■
5. Даны вершины треугольника А (-2;5) , В (2;1) , С (0;-3). Составить уравнение прямой, проходящей через вершину С перпендикулярно вектору .
□
Воспользуемся
уравнением прямой, проходящей через
заданную точ-ку
перпендикулярно нормальному вектору
прямой
:
.
Заданной точкой
является вершина
,
а за нормальный вектор можно взять
вектор
:
.
Тогда
или
.
■
6. Даны координаты вершин пирамиды: А (14;5;6), В (-2;4;2), С (4;5;7),
D (7;8;4). Составить уравнение сечения пирамиды, проходящего через вершину В перпендикулярно ребру CD . Найти длину этого ребра.
□
Сечением пирамиды является некоторая плоскость, проходящая че-рез вершину В перепендикулярно ребру CD .
Воспользуемся
уравнением плоскости, проходящей через
заданную точку
перпендикулярно нормальному вектору
плос-кости
:
.
Заданной точкой
является вершина
,
а за нормальный век-тор можно взять
вектор
:
.
Тогда
,
или
.
Длиной ребра
является модуль вектора
:
.
■
7. Найти фокусы, полуоси, эксцентриситет кривой второго порядка. Сделать рисунок
.
□
В заданном
уравнении
.
Составим выраже-ние:
.
Следовательно, заданное уравнение второго порядка описывает кри-вую эллиптического вида. Преобразуем заданное уравнение:
Получили каноническое уравнение эллипса, т.к.
каноническое
уравнение эллипса,
Фокусы:
Тогда
Полуоси:
большая полуось,
малая полуось .
Эксцентриситет:
.
■
8. Составить
уравнение параболы, которая имеет фокус
и проходит через начало координат.
Сделать рисунок.
□
Так как фокус параболы лежит на оси Оу, то парабола симметрична относительно оси Оу. Уравнение параболы, симметричной относи-тельно оси Оу имеет вид:
.
Из выражения
фокуса параболы
следует, что
,
.
Следовательно, уравнение параболы будет
иметь вид:
или
.
■
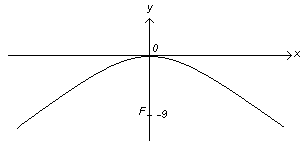
ЛИТЕРАТУРА
1. Минорский В.П. Сборник задач по высшей математике. – М.: Наука, 1987. – 352 с.
2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в уп- ражнениях и задачах. Ч.1. – М.: Высшая школа, 1986. – 304с.
3. Клетеник Д.В. Сборник задач по аналитической геометрии. – М.: Наука, 1986. – 224 с.
Электронное пособие
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к самостоятельной работе
по дисциплине
“ ВЫСШАЯ МАТЕМАТИКА “
( Линейная алгебра и аналитическая геометрия )
для студентов дневной формы обучения специальностей
направления 6.050102 “Компьютерная инженерия”
Составитель:
Александр Евгеньевич Богданов
Редактор А.Е. Богданов
Техн. редактор А.Е. Богданов
Оригинал – макет А.Е. Богданов
Северодонецк 2007