2. Симметричный оператор.

Линейный оператор называется симметричным, если для любых векторов и выполняется равенство: .

Теорема. Для того, чтобы линейный оператор был симметричен, необходимо и достаточно, чтобы его матрица в ортогональном пространстве была симметрична.

Рассмотрим для простоты двухмерное пространство. Линейные операторы ₁ и ₂ определены своими матрицами

и

Вычислим векторы ₁( ) и ₂( )

Найдем скалярные произведения :

Найдем разность скалярных произведений:

(1)

Если эта разность равна 0, то будут выполняться равенства (необходимость)

₁₁= b₁₁, ₂₁ = b₁₂, , ₂₂=b₂₂ (2) и обратно, если только что записанные соотношения выполнены для любых и , то и равенство (1) выполнено (достаточность). Система равенств (2) означает, что

3. Ортогональность собственных векторов.

Теорема: собственные векторы симметричного линейного оператора, соответствующие различным собственным числам, взаимно ортогональны.

Пусть векторы и - собственные векторы оператора соответствующие собственным числам λ₁ и λ₂, причем λ₁≠λ₂ . По определению симметричного оператора:

. Подставляя сюда и получим . Вынесем λ₁ и λ₂ за знак скалярного произведения, перенесем все влево и разложим на множители и получим , так как λ₁≠λ₂ , то =0, что означает взаимную ортогональность векторов и .

3.7.Квадратичные формы.

Пусть L=( )- симметричная матрица n-го порядка, тогда выражение -называется квадратичной формой переменных x₁,x₂...x_n. Матрица L=( _ij) i,j=(1,2...n) -называется матрицей квадратичной формы. Пусть( ) –симметричная матрица, т.е. = . В матричной форме квадратичная форма имеет вид :

, где X= -матрица столбец переменных, а = - матрица строка этих же переменных. Найдем произведение этих матриц.

-что является по определению квадратичной формой.

Канонический вид квадратичной формы

Следует отметить, что с помощью некоторых линейных преобразований квадратичную форму можно привести к наиболее простому каноническому виду. Квадратичная форма называется канонической, если все ее коэффициенты при i ≠ j ,т.е.

матрица канонической квадратичной формы является диагональной.

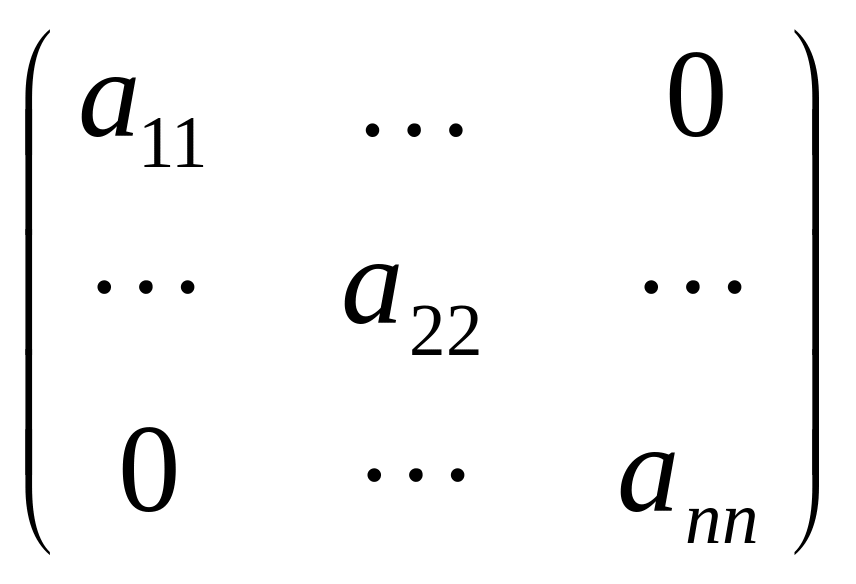
Теорема. Любая квадратичная форма с помощью линейных преобразований может быть приведена к каноническому виду.

Канонический вид квадратичной формы не является однозначно определенным, так как одна и та же квадратичная форма может быть приведена к каноническому виду многими способами. Однако полученные различными способами канонические формы обладают рядом общих свойств. Одно из них - закон инерции квадратичных форм формулируется в виде теоремы.

Теорема (закон инерции квадратичных форм). Число слагаемых с положительными (отрицательными) коэффициентами квадратичной формы не зависит от способа приведения формы к этому виду.