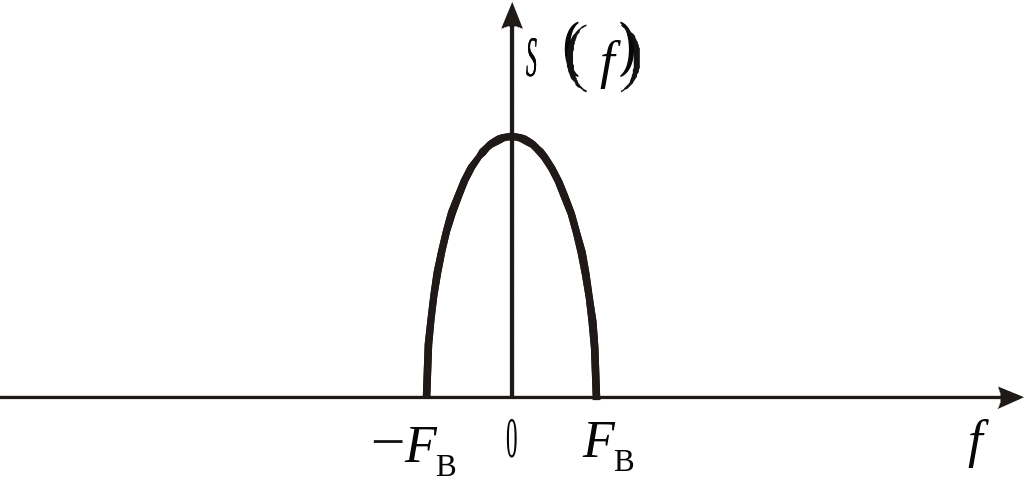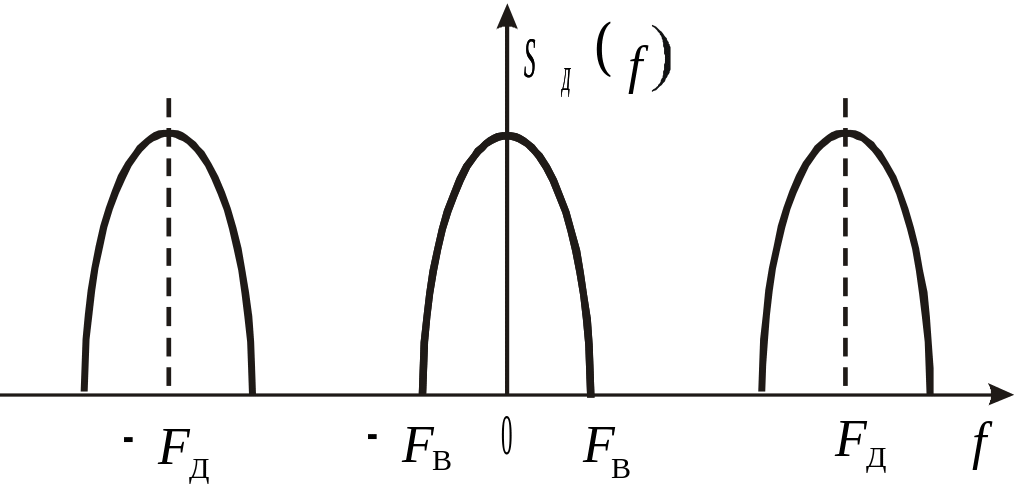4. Лабораторная работа № 4 восстановление сигналов по дискретным отсчетам

Цель работы. Изучение и экспериментальная проверка основных положений теории дискретизации и восстановления сигналов по дискретным отсчетам. Исследование влияния частоты отсчетов, типа восстанавливающего фильтра и его характеристик на точность восстановления сигналов.

5.1. Теоретические сведения

5.1.1. Дискретизация сигналов

Для точного представления произвольного непрерывного сигнала на конечном интервале необходимо располагать данными о мгновенных значениях (отсчетах) этого сигнала во всех точках интервала, т.е. непрерывным множеством отсчетов, отстоящих друг от друга на бесконечно малые интервалы. Некоторое приближенное представление о сигнале можно составить по его отображению в виде дискретной последовательности импульсов, имеющих на интервалах значения , называемых отсчетами. Операция замены непрерывного сигнала последовательностью его мгновенных значений называется дискретизацией.

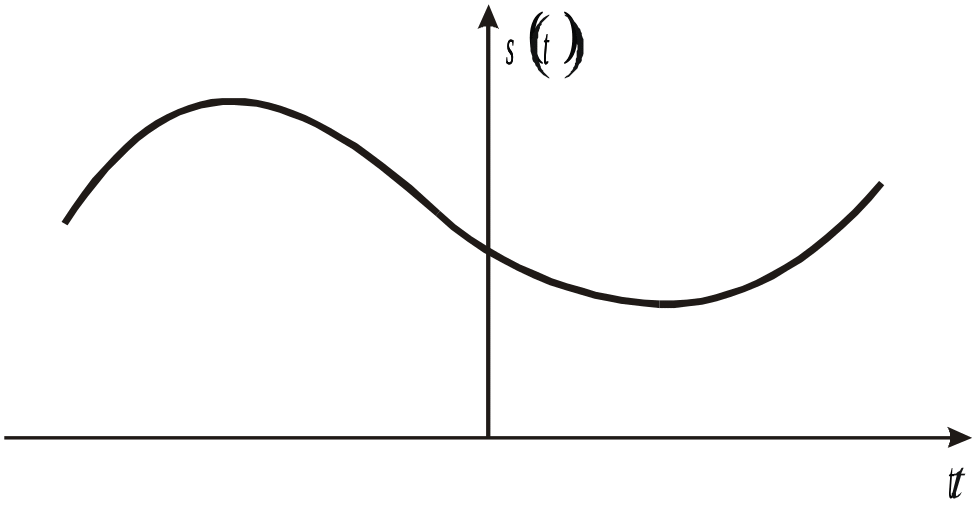
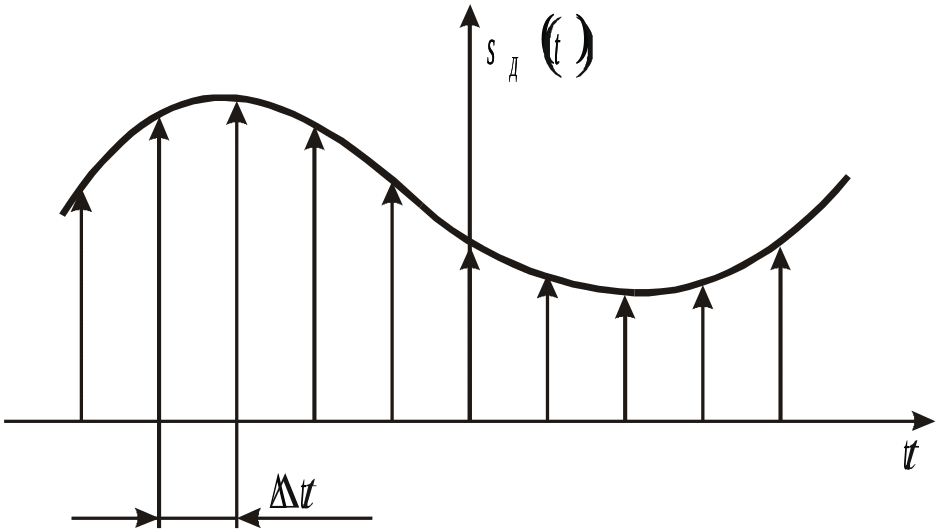
На рисунке 5.1 показан исходный сигнал (рис. 5.1,а) и его спектр (рис.5.1,б). В результате дискретизации исходный сигнал преобразуется в совокупность отсчетов (рис. 5.1,в), аналитически описываемую с помощью дельта-функций:

, (5.1)

где - интервал между соседними отсчетами. Спектр дискретизированного сигнала (рис. 5.1,г) представляет собой сумму копий исходного спектра сигнала (рис.5.1,б), расположенных вблизи центральных частот , ( ).

Для неискаженного воспроизведения сигнала по последовательности отсчетов посредством идеального фильтра низких частот необходимо выбирать частоту дискретизации так, чтобы спектральные компоненты располагались в неперекрывающихся областях (рис. 5.1,г). Этому соответствует значения . При спектральные области перекрываются, в полосу частот дискретизируемого сигнала попадут спектральные компоненты смежных областей и возникнут искажения при восстановлении сигнала по отсчетам.

Для точного воспроизведения непрерывных сигналов с ограниченным (финитным) спектром достаточно располагать значениями сигнала (отсчетами) лишь в отдельных точках. Модели сигналов с ограниченным спектром часто используются в технике связи.

а)	б)
в)	г)

Рис. 5.1. Спектральное представление дискретизированного сигнала: а) исходный сигнал; б) спектр исходного сигнала; в) дискретизированный сигнал; г) спектр дискретизированного сигнала

В частности, в стандартном телефонном канале за верхнюю граничную частоту принимают Гц, при телевизионной передаче граничная частота определяется числом различимых элементов изображения и равна МГц.

5.1.2. Теорема отсчетов

Фундаментальное значение для решения многих задач теории передачи сигналов имеет следующая теорема отсчетов Котельникова¹: непрерывный сигнал , не содержащий в своем спектре частот выше , полностью определяется отсчетами мгновенных значений в точках, отстоящих друг от друга на интервалы . Эта теорема позволяет представить непрерывный сигнал в виде ряда

. (5.2)

Отсчеты сигнала могут рассматриваться как коэффициенты обобщенного ряда Фурье, разложения сигнала по ортогональной системе функций

, (5.3)

называемых иногда функциями Котельникова.

Процедура восстановления непрерывного сигнала по отсчетам его мгновенных значений вытекает непосредственно из (5.2): необходимо перемножить значения отсчетов на соответствующие отсчетные функции (5.3) и просуммировать полученные произведения.

Для полного восстановления необходимо просуммировать бесконечное множество членов ряда (5.2). Однако, если функция с ограниченным спектром рассматривается на конечном интервале , то точное разложение (5.2) можно заменить следующим приближенным разложением:

.

Конечное число отсчетов , определяющее , равно (при )

.

Очевидно, что погрешность представления сигнала при ограничении числа его отсчетов будет тем меньше, чем больше число слагаемых учитывается при суммировании.

При практическом применении метода дискретизации сигналов и их восстановлении неизбежно возникают погрешности. Основные причины возникновения погрешностей следующие:

1. Сигналы с ограниченным спектром бесконечны во времени и поэтому восстановление мгновенного значения принципиально требует учета бесконечно большого числа отсчетов. Использование числа отсчетов, взятых на ограниченном интервале (0, ) означает переход к конечному числу отсчетов в ряду (5.2), что и вызывает появление ошибки при восстановлении.

2. Сигналы конечной длительности принципиально обладают бесконечно широким спектром . Поэтому за обычно принимают частоту, при которой в диапазоне , сосредоточена основная (заданная) энергия сигнала. Очевидно, что погрешность восстановления будет тем больше, чем медленнее убывают спектральные компоненты сигнала за пределами выбранной полосы частот .

3. Отклонение характеристик реальных фильтров нижних частот от идеальных также приводит к появлению дополнительных погрешностей восстановления сигнала по дискретным отсчетам.

АЧХ идеального фильтра низких частот (ФНЧ) равномерна

(5.4)

а ФЧХ – линейна .

Импульсная характеристика идеального фильтра с коэффициентом передачи (5.4) с точностью до постоянного множителя описывается функцией отсчетов , т.е.

. (5.5)

4. Кроме перечисленных причин могут так же возникать погрешности восстановления, обусловленные тем, что форма импульсов дискретизирующей последовательности отличается от дельта-импульсов, что может приводить к искажениям спектральных характеристик.