2.4. Контрольные вопросы

1. Дайте определение ортонормированной системы базисных функций.

2. Дайте определение спектра сигнала.

3. Каким образом разложение в тригонометрический ряд Фурье периодической функции может быть обобщено на случай разложения непериодических функций?

4. Какими свойствами обладает спектральная плотность вещественного сигнала?

5. В чем состоит характерная особенность спектра дельта-импульса?

6. Как по известным спектральным плотностям двух сигналов вычислить их скалярное произведение?

7. Какова связь между длительностью импульса и шириной его спектра?

8. Как в частотной области отображаются операции дифференцирования и интегрирования сигналов?

3. Лабораторная работа № 2 Корреляционный анализ детерминированных сигналов

Цель работы. Изучить свойства автокорреляционной и взаимной корреляционной функции сигналов. Изучить методы формирования и построить корреляционные функции реальных сигналов.

3.1. Теоретические сведения

При исследовании сигналов часто оказывается необходимой характеристика, которая дает представление о свойствах сигнала во временной области, в частности, о скорости изменения во времени, о длительности сигнала и т.п. В качестве такой временной характеристики широко используется корреляционная функция сигнала. Для детерминированного сигнала конечной длительности корреляционная функция определяется следующим образом

, (3.1)

где – временной сдвиг сигнала, * – знак комплексного сопряжения.

Для вещественных сигналов знак комплексного сопряжения можно опустить и выражение для корреляционной функции запишется в виде

. (3.2)

Величина характеризует степень связи (корреляции) сигнала со своей копией, сдвинутой на величину по оси времени. Функция достигает максимума при и

, (3.3)

т.е. максимальное значение корреляционной функции равно энергии сигнала. С увеличением убывает (не обязательно монотонно) и при относительном сдвиге сигналов и на время, превышающее длительность сигнала, обращается в нуль.

На рис.3.1 показано построение корреляционной функции для простейшего сигнала в виде прямоугольного импульса (рис.3.1,а). Сдвинутый на (в сторону опережения) сигнал показан на рис. 3.1,б, а произведение — на рис.3.1,в. График функции изображен на рис. 3.1,г. Значение текущего отсчета корреляционной функции равно площади под кривой, ограниченной функцией . Численное значение таких площадей для соответствующих и дают координаты функции .

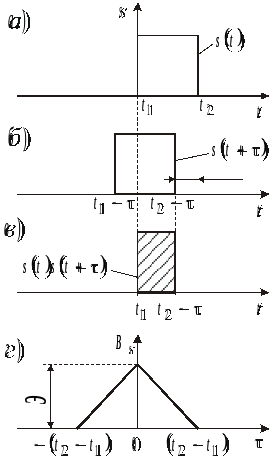
Рис.3.1. Построение корреляционной функции для прямоугольного импульса

Выражение (3.2) можно обобщить следующим образом

. (3.4)

Из (3.4) следует, что функция является четной.

Для периодического сигнала, энергия которого бесконечно велика, определение корреляционной функции в виде (3.3) неприемлемо. В этом случае исходят из следующего определения

. (3.5)

При таком определении корреляционная функция приобретает размерность мощности, причем равна средней мощности периодического сигнала. Ввиду периодичности сигнала усреднение произведения или по бесконечно большому отрезку должно совпадать с усреднением по периоду . Поэтому выражение (3.5) можно заменить выражением

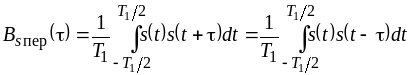. (3.6)

Интегралы 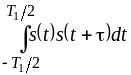и 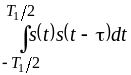представляют собой на интервале корреляционную функцию сигнала . Тогда

.

Периодическому сигналу соответствует и периодическая корреляционная функция . Период функции совпадает с периодом исходного сигнала . Например, для простейшего гармонического сигнала корреляционная функция запишется в виде

,

.

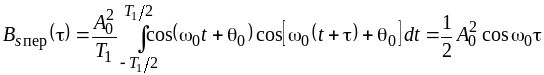При значение корреляционной функции есть средняя мощность гармонического колебания с амплитудой . Величина корреляционной функции гармонического сигнала не зависит от начальной фазы колебания.

На рис.3.2 изображен сигнал в виде последовательности прямоугольных импульсов и его корреляционная функция. Каждый из импульсов функции совпадает по форме с корреляционной функцией одиночного импульса из периодической последовательности . Однако в данном случае максимальные ординаты равны не энергии сигнала, а средней мощности сигнала , т.е. величине .

Рис.3.2. Периодическая последовательность импульсов и ее корреляционная функция

Для оценки степени связи между двумя различными сигналами и используется взаимная корреляционная функция, определяемая как

. (3.7)

Для вещественных функций и

. (3.8)

Корреляционная функция является частным случаем взаимной корреляционной функции при и часто называется автокорреляционной функцией.

На рис.3.3 представлен пример построения взаимной корреляционной функции. На рис. 3.3,а показано положение сигналов при . При сдвиге сигнала влево ( , рис. 3.3,б) корреляционная функция сначала возрастает, а затем убывает до нуля при . При сдвиге вправо ( ) корреляционная функция сразу убывает. В результате получается асимметричная относительно оси ординат функция (рис. 3.3,в).

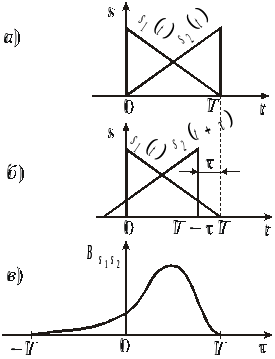
Рис.3.3. Построение взаимной корреляционной функции сигналов

Выражение (3.8) можно обобщить следующим образом

. (3.9)

В отличие от автокорреляционной функции взаимная корреляционная функция не обязательно является четной и не обязательно достигает максимума при .

Установим связь между корреляционной функцией и спектральными характеристиками сигнала. Используя выражение для связи между произведением функций и произведением спектров

и полагая , и соответственно , , получим

.

Поскольку , приходим к искомому соотношению

. (3.10)

На основании свойств преобразования Фурье можно записать

. (3.11)

Таким образом, прямое преобразование Фурье корреляционной функции дает спектральную плотность энергии, а обратное преобразование Фурье дает корреляционную функцию.

Из выражений (3.10) и (3.11) вытекают следующие свойства корреляционной функции:

1. Чем шире спектр сигнала , тем меньше интервал корреляции, т.е. сдвиг , в пределах которого корреляционная функция отличается от нуля. Соответственно чем больше интервал корреляции, тем уже спектр сигнала.

2. Корреляционная функция не зависит от фазочастотного спектра сигнала, т.е. различным по форме сигналам , обладающим одинаковыми амплитудными спектрами, соответствуют одинаковые корреляционные функции .