10.1.2. Передаточная функция оптимального фильтра

Под синтезом фильтра будем понимать отыскание передаточной функции физически осуществимого фильтра, обеспечивающего максимизацию отношения сигнал/помеха. Передаточную функцию будем представлять в виде . Наиболее просто данная задача решается для сигнала, действующего на фоне белого шума с равномерным спектром . Для отыскания оптимальной передаточной функции составим выражения для сигнала и шума на выходе фильтра сначала порознь, а затем в виде их соотношения.

Сигнал в фиксированный момент времени определим общим выражением

,

(10.1)

а среднеквадратическое значение помехи – выражением

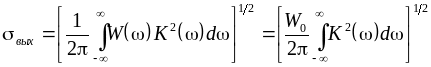. (10.2)

В выражении (10.1) – спектральная плотность заданного входного сигнала , а под подразумевается момент времени (пока не определенный), соответствующий максимуму (пику) сигнала на выходе фильтра.

Составим теперь соотношение

. (10.3)

Воспользуемся неравенством Шварца

, (10.4)

где и – в общем случае комплексные функции. Это неравенство обращается в равенство только при выполнении условия

, (10.5)

т.е. когда функция пропорциональна функции, комплексно-сопряженной ( – произвольный постоянный коэффициент).

Приравнивая в (10.4) и , запишем (10.4) в форме

.

Тогда выражение (10.3) позволяет составить следующее неравенство:

(10.6)

Учитывая, что выражение определяет полную энергию входного сигнала , приходим к следующему результату

(10.7).

Из выражения (10.5) следует, что выражение (10.7) обращается в равенство при выполнении условия

или

. (10.8)

Полученное соотношение полностью определяет передаточную функцию фильтра, максимизирующего отношение сигнал/помеха на выходе при входной помехе в виде белого шума. Функция , отвечающая условию (10.8), согласована с характеристиками сигнала. Поэтому рассматриваемый фильтр часто называют согласованным фильтром.

Отношение пика сигнала к среднеквадратическому отношению помехи на выходе фильтра определяется равенством

. (10.9)

Из соотношения (10.8) вытекают следующие требования к фильтру:

1. ФЧХ фильтра должна удовлетворять условию

; (10.10)

2. АЧХ должна удовлетворять условию

. (10.11)

В случаях, когда под комплексной передаточной функцией подразумевается безразмерная величина, постоянный коэффициент должен иметь размерность, обратную размерности спектральной плотности сигнала.

Соотношения (10.10) и (10.11) обладают следующим физическим смыслом. Соотношение (10.10) можно назвать условием компенсации начальных фаз в спектре сигнала, поскольку фазовый сдвиг в фильтре равен по величине и обратен по знаку начальной фазе соответствующей составляющей спектра входного сигнала. В результате прохождения сигнала через фильтр с фазовой характеристикой сложение всех компонентов спектра, скорректированных по фазе, образует пик выходного сигнала.

Соотношение (10.11) устанавливает, что АЧХ фильтра должна по своей форме совпадать с амплитудным спектром сигнала . Благодаря этому фильтр пропускает спектральные составляющие шума с тем большим ослаблением, чем меньше модуль . Это приводит с существенному уменьшению мощности шума на выходе фильтра. Ослабление сигнала из-за неравномерности характеристики выражено в меньшей степени, чем ослабление шума, поскольку уменьшение имеет место для спектральных составляющих, вклад которых в пиковое значение сигнала сравнительно мал. В результате получается ослабление шума относительно сигнала. В сочетании с устранением фазовых сдвигов между спектральными составляющими сигнала это приводит к максимизации отношения сигнал/шум на выходе фильтра.