2. Лабораторная работа №1 спектральный анализ детерминированных сигналов

Цель работы. Изучить методы спектрального анализа периодических и непериодических сигналов. Исследовать спектральные характеристики детерминированных сигналов.

2.1. Спектральное представление сигналов

2.1.1. Общие сведения об ортогональных сигналах и обобщенном ряде Фурье

Основу большинства используемых в радиотехнике моделей сигналов составляют ортогональные сигналы. Два сигнала и называются ортогональными, если их скалярное произведение, а значит и взаимная энергия равны нулю

.

Допустим, в гильбертовом пространстве задано бесконечное число (система) функций, попарно ортогональных на интервале и обладающих единичными нормами

(2.1)

В этом случае говорят, что в пространстве сигналов задан ортонормированный базис. Разложим произвольный сигнал в ряд

. (2.2)

Представление (2.2) называют обобщенным рядом Фурье сигнала в выбранном базисе. Коэффициенты этого ряда находят следующим образом. Возьмем базисную функцию с произвольным номером , умножим на нее обе части равенства (2.2) и затем проинтегрируем результаты по интервалу , в котором заданы базисные функции. Получим

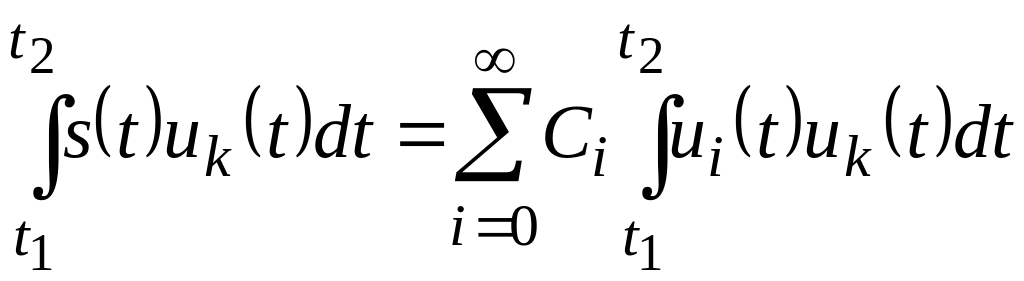. (2.3)

Ввиду ортонормированности базиса в правой части выражения (2.3) остается только одно слагаемое с номером

, (2.4)

Поэтому использование обобщенного ряда Фурье позволяет при изучении сигналов перейти от рассмотрения бесконечного числа значений сигнала к рассмотрению коэффициентов обобщенного ряда Фурье.

Чаще всего в радиотехнике в качестве базисных функций используют тригонометрические функции ортогональные на интервале , где - период разлагаемой в ряд функции .

2.1.2. Спектральное представление периодических колебаний

При формировании и обработке сигналов часто приходится иметь дело с периодическими колебаниями сложной формы. Периодическую функцию можно представить разложением в обобщенный ряд Фурье (2.2) по базисным функциям основной тригонометрической системы

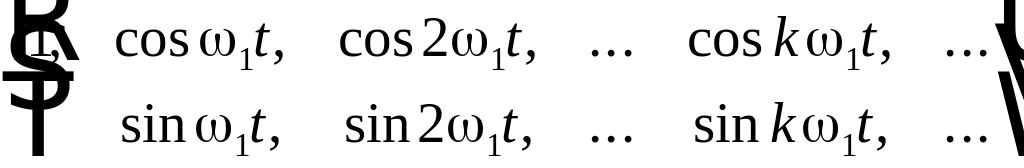. (2.5)

Все функции системы (2.5) попарно ортогональны на интервале . Обобщенный ряд Фурье по базисным функциям (2.5) можно записать

, (2.6)

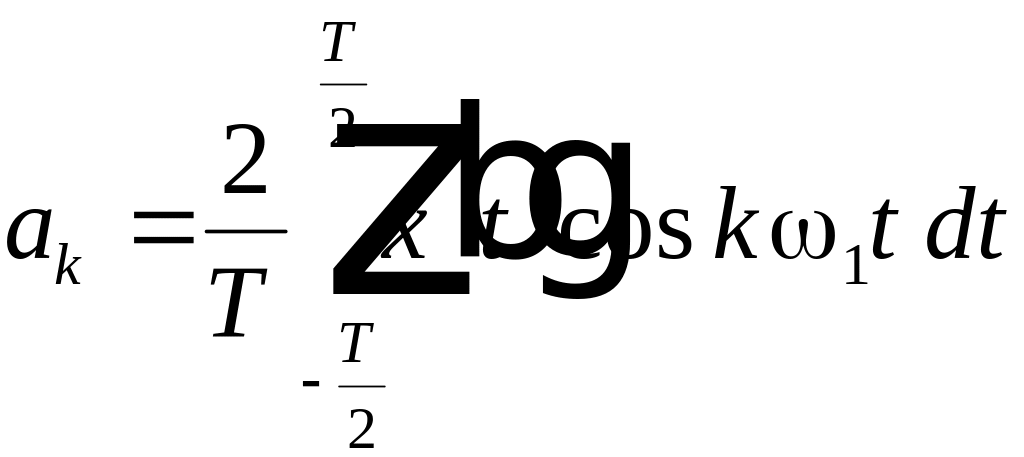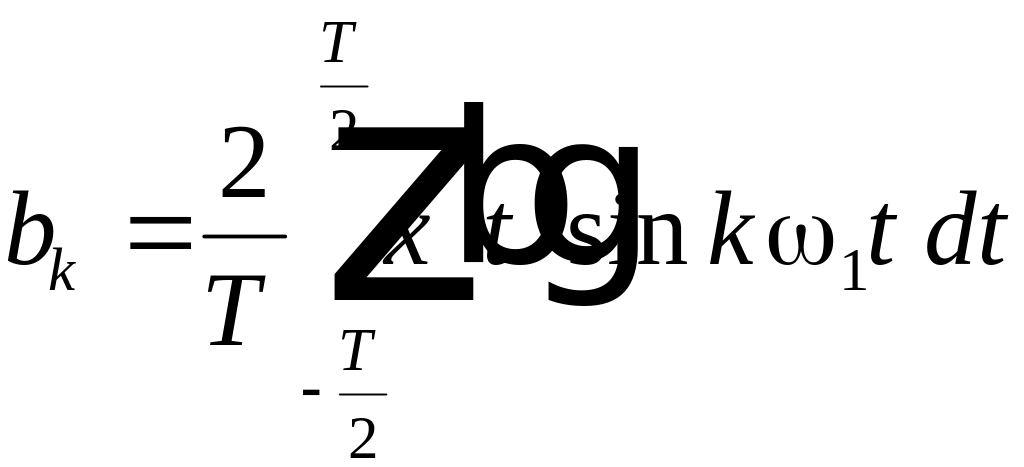; . (2.7)

Представление (2.6) называют рядом Фурье. Ряд (2.6) можно записать в виде

, (2.8)

где

, , . (2.9)

Согласно формуле (2.8) периодическую функцию можно представить суммой гармонических колебаний с частотами, кратными основной частоте с амплитудами и начальными фазами . Совокупность амплитуд образует амплитудный спектр сигнала, а совокупность фаз - фазовый спектр сигнала. Линейчатый амплитудный спектр периодического сигнала изображен на рис. 2.1. Ряд Фурье (2.8) часто представляют в комплексной форме

, (2.10)

где - комплексная амплитуда, определяемая по формуле

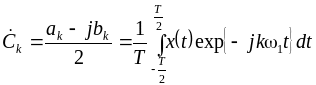. (2.11)

Следует обратить внимание на то, что сумма в (2.10) охватывает не только положительные значения , но и отрицательные (появляются "отрицательные частоты").

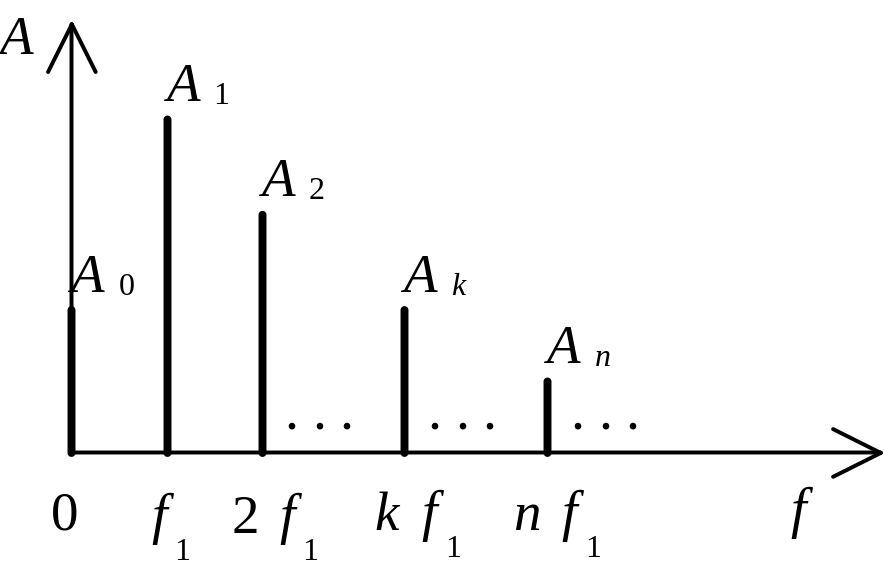
Рис. 2.1. Амплитудный спектр периодического сигнала с периодом следования

Для перехода от (2.8) к (2.10) можно воспользоваться формулой Эйлера

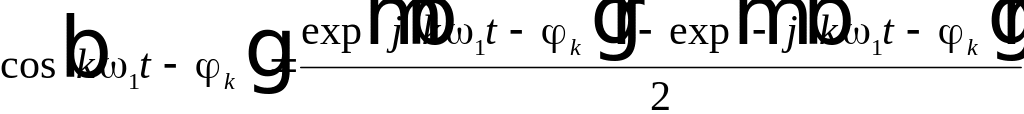. (2.12)

Выражение (2.12) можно интерпретировать как представление гармонического сигнала единичной амплитуды с положительной частотой в виде суммы двух гармонических колебаний (половинной амплитуды) на положительной частоте и отрицательной частоте . Комплексное представление ряда Фурье оказывается очень удобным при выполнении различных расчетов.