8.1.3. Метод укороченного уравнения автогенератора
При больших уровнях сигнала в автогенераторе пренебрегать нелинейностью характеристики усилительного элемента схемы нельзя. Дифференциальные уравнения, описывающие работу автогенератора в этом случае получаются нелинейными, решение которых в общем случае не найдено. Поэтому пользуются приближенными методами решения.
Если зависимость
нелинейная, то, обращаясь снова к
уравнениям (8.1 и 8.3)
и учитывая, что
,
получим нелинейное дифференциальное
уравнение автогенератора, описывающее
его работу при любых режимах.
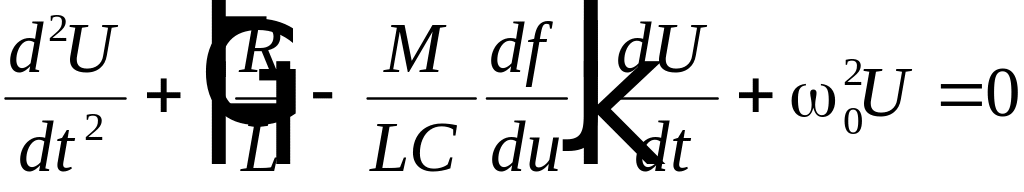(8.7)
Приближенное решение этого уравнения будем искать с учетом того обстоятельства, что из-за высокой добротности контура и несмотря на нелинейность характеристик усилительного элемента выходное колебание в схеме все равно будет иметь гармонический характер
.
(8.8)
Причем из-за
инерционности контура изменения
амплитуды происходит очень медленно
(выполнено условие
),
а колебания генерируются с собственной
частотой контура
.
Тогда
,
или, учитывая условие , приближенно
.
Подставив эти значения в исходное уравнение, получаем
,
(8.9)
так называемое укороченное уравнение, приближенно описывающее процессы в автогенераторе с высокодобротным колебательным контуром.
8.1.4. Средняя крутизна
Все процессы в схеме автогенератора периодические, поэтому и ток усилительного элемента может быть представлен рядом Фурье
,
или, учитывая избирательные свойства контура можем отбросить все высшие гармоники тока, которые на работу схемы практически не влияют. Тогда
.
Представив
,
,
после подстановки
получим
.
Величину
называют средней
крутизной
транзистора или крутизной по первой
гармонике. Вводя эту крутизну в укороченное
уравнение генератора, имеем:
. (8.10)
Если
известна зависимость
,
то можно найти выражение для средней
крутизны
,
и подставив ее в последнее уравнение,
найти его решение.
8.1.5. Стационарный режим автогенератора
В стационарном
режиме работы автогенератора амплитуда
колебаний постоянна и, следовательно,
в уравнении (8.10)
,т.е.
.
(8.11)
Экспериментально
полученные зависимости
могут иметь вид, аналогичный одному из
графиков, представленных на рис. 8.4.
а) |
б)
|
Рис. 8.4. К определению средней крутизны
Не выполняя подробного исследования, отметим только, что первый из графиков соответствует работе автогенератора в мягком режиме, второй – работе автогенератора в жестком режиме. Причем одна из точек на втором графике (точка-1) соответствует неустойчивой стационарной амплитуде автогенератора, а вторая – устойчивой стационарной амплитуде. Можно показать, что мягкий режим получается всегда при выборе исходной рабочей точки в середине линейного участка характеристики , где крутизна максимальна.
В переходном режиме амплитуда колебаний автогенератора изменяется по закону
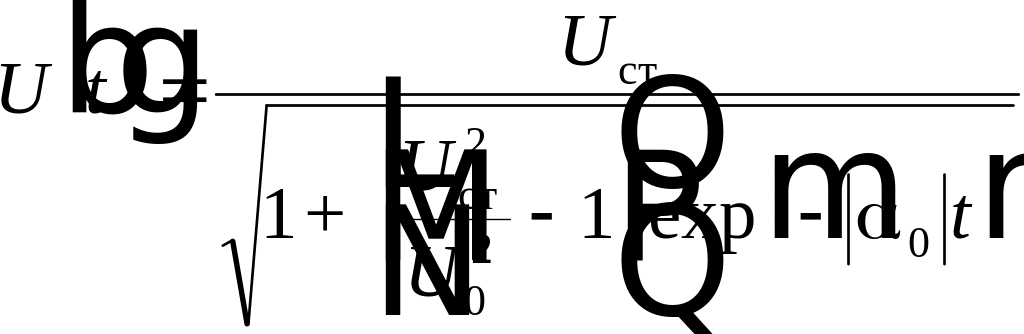, (8.12)
где
-
стационарная амплитуда колебаний
автогенератора;
-
начальная амплитуда колебаний
автогенератора;
- параметр, характеризующий эквивалентное
затухание в схеме автогенератора.
Характер изменения амплитуды колебаний
в автогенераторе зависит от соотношения
начальной и установившейся амплитуды
колебании. Если при
,
то в системе без переходного процесса
устанавливается стационарный режим.
Если
- то колебания нарастают до
.
При
колебания опадают до
.