5.4.4. Однопродуктовая динамическая модель управления запасами
В этой модели предполагается, что спрос на поставляемую (производимую) продукцию известен, но он может меняться от этапа к этапу. Например, предприятие производит партиями некоторые изделия. Размеры заказов значительно меняются от месяца к месяцу. Поэтому иногда лучше выполнять заказ нескольких месяцев одной партией (учитывая затраты на переналадку оборудования), а затем хранить, чем выполнять заказ именно в тот месяц, когда он должен быть отправлен. Необходимо составить план производства на указанные N месяцев с учетом затрат на переналадку оборудования, производство и хранение изделий.
Обозначим: j – номер периода (месяца), j=1,..,N;
j – число изделий, производимых в j-й месяц;
xj-1 – величина запаса к началу j-го месяца;
dj – спрос на изделия в j-й месяц;
fj(xj, j) – затраты на переналадку, производство и хранение в j-й месяц, а именно:
(5.19)
где
– затраты на переналадку оборудования
(либо оформление заказа) в j-ом
периоде;
j(xj) = hjxj – затраты на хранение xj единиц продукции,
hj – затраты на хранение единицы запаса, переходящей из периода j в j+1;
j(j) – затраты на производство (закупку) j единиц продукции в периоде j.
Кроме того, будем считать известными величины запасов к началу первого периода x0 и к концу последнего xN.
Задача УЗ состоит в том, чтобы найти план производства (закупки)
…N
и хранения
x1…xN-1,
удовлетворяющий уравнению баланса
xj = xj-1 + j – dj; j=1,..,N (5.20)
и минимизирующий суммарные затраты за весь период
(5.21)
при очевидных дополнительных условиях
xj0; j; j=1,..N (5.22)
0 xj dj + dj+1 + .. + dN (5.23)
0jdj + xj (5.24)
В общем случае задача (5.20)-(5.24) представляет собой задачу нелинейного программирования. Кроме того, если переменные xj, j могут принимать только целые значения, то получим задачу целочисленного нелинейного программирования.
Будем решать задачу (5.20)-(5.24) методом динамического программирования.
Обозначим
– минимальные затраты за первые k
периодов. Тогда справедливо уравнение
Беллмана
(5.25)
Решение уравнения Беллмана (5.25) осуществляется в два этапа.
Пример 5.5. Рассмотрим задачу управления запасами в течение одного квартала по месяцам (N=3). Исходные данные поместим в таблицу
J |
1 |
2 |
3 |
dj |
3 |
6 |
2 |
Kj |
6 |
8 |
7 |
hj |
4 |
3 |
5 |
(5.26)
x0 = 1; x3 = 0.
Решение.
1-й этап решения уравнения Беллмана.
Пусть K=1, тогда
(4.27)
– минимальные затраты по управлению запасами в течение первого месяца при условии, что запас к концу первого месяца составит x1 единиц.
На основании уравнения баланса (5.20) имеем
x1 = x0 + 1 - d1 = 1 + 1 - 3 = 1 - 2, т.е.
x1) = x1 + 2 (5.28)
оптимальное производство (пополнение) в первом месяце в зависимости от запаса к концу месяца.
Далее, т.к. x1 = 1 - 2 0, то 1 2, следовательно
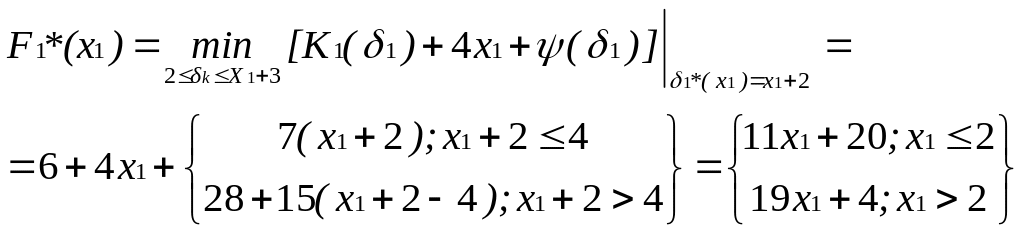(5.29)
Пусть K=2, тогда
– минимальные затраты по управлению
запасами в течение двух
первых месяцев квартала, при условии,
что запас к концу второго месяца составит
x2 единиц.
Подставляя в выражение для Fx2)
числовые данные, получим
(5.30)
Для определения F2*(x2) строим таблицу 5.4.1 для x2 = {0, 1, 2}.
Обозначим
Таблица 5.4.1
-
x2
2
x1
K2(2)+3x2+(2)+F1*(x1)
=F2(x2,2)
F2*(x2)
2*(x2)
0
6
0
0
0
118
118
1
5
8
0
7
99
114
2
4
8
0
14
80
102
0
3
3
8
0
21
61
90
78
4
4*
2
8
0
28
42
78*
5
1
8
0
43
31
82
6
0
8
0
58
20
86
0
7
0
3
0
137
140
1
6
8
3
7
118
136
2
5
8
3
14
99
124
3
4
8
3
21
80
112
1
4
3
8
3
28
61
100
96
5
5*
2
8
3
43
42
96*
6
1
8
3
58
31
100
7
0
8
3
73
20
104
0
8
0
6
0
156
162
1
7
8
6
7
137
158
2
6
8
6
14
118
146
3
5
8
6
21
99
134
2
4
4
8
6
28
80
122
114
6
5
3
8
6
43
61
118
6*
2
8
6
58
42
114*
7
1
8
6
73
31
118
8
0
8
6
88
20
122
Наконец, пусть K = 3, тогда
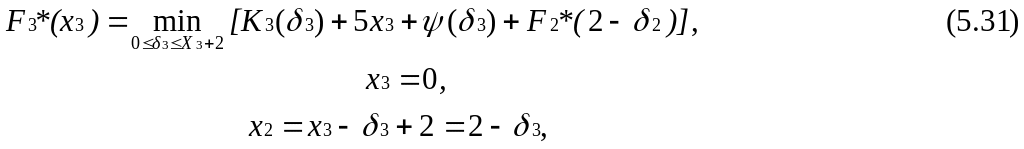
где F3*(x3) – минимальные затраты по управлению запасами в течение квартала.
Обозначим
и строим таблицу 5.4.2.
Таблица 5.4.2
x3 |
3 |
x2 |
K3+(2)+F2*(x2) |
=F3(x3,3) |
F3*(x3) |
3*(x3) |
||
|
0 |
2 |
0 |
0 |
114 |
114 |
|
|
0 |
1 |
1 |
7 |
7 |
96 |
110 |
99 |
2 |
|
2* |
0 |
7 |
14 |
78 |
99* |
|
|
2-й этап решения уравнения Беллмана.
Итак, из таблицы 5.4.2 имеем, что
3* = 2; x3 = 0; F3* = 99.
Далее из уравнения баланса находим
x2 = x3 - 3* + 2 = 0 - 2 + 2 = 0.
Из табл.5.4.1
2* (x2 = 0) = 4.
Из уравнения баланса
x1 = x2 - 2* + 6 = 0 - 4 + 6 = 2.
Далее по формуле (5.28) находим
1* (x1 = 2) = 2 + 2 = 4,
и из уравнения баланса имеем
x0 = x1 - 1* + 3 = 2 - 4 + 3 = 1,
что соответствует исходному запасу.
Итак, стратегия пополнения запасов состоит в следующем:
1-й месяц. 1* = 4, из них 2 единицы покрывают спрос (x0 = 1), 2 единицы остаются в запасе (x1 = 2).
2-й месяц 2* = 4, что позволяет покрыть спрос данного месяца (x1=2;d2=6), запаса нет.
3-й месяц. 3* = 2, что соответствует потребности данного периода (d3 = 3).
ОС (оптимальная стратегия) =
.
ОТ (оптимальная траектория) = X* = (x0, x1, x2, x3) = (1, 2, 0, 0).
Оптимальные расходы составляют 99 денежных единиц.
Домашнее задание 13.
В заданиях 1-10 решить задачу из примера 5.5 при соответствующих условиях.
x3 = 1.
x0 = 0.
Спрос задан вектором d=(4,6,2).
Решить задачу из примера 5.5 для следующих исходных данных:
J |
1 |
2 |
3 |
dj |
5 |
3 |
4 |
Kj |
6 |
8 |
7 |
hj |
3 |
3 |
4 |
x3 = 3.
x0 = 0, x3 = 0.
h = (2 ,3, 2).
K = (5, 6, 4).
x0 = 0, x3 = 2.
d = (1, 7, 6).