
- •Вопрос 2. Аксиоматическое определение вероятности. Классическое, статистическое, геометрическое определение вероятности события.
- •Вопрос 3. Свойства вероятности. Теоремы сложения и умножения вероятностей. Независимые события. Условная вероятность. Вероятность наступления хотя бы одного из событий.
- •Вопрос 4. Формула полной вероятности. Формула Байеса (вероятности гипотез).
- •Вопрос 5. Повторные независимые испытания. Формула Бернулли. Полиномиальная формула. Наивероятнейшее число появлений события в независимых испытаниях.
- •Вопрос 7. Применение интегральной теоремы Муавра-Лапласса. Отклонение относительной частоты от постоянной вероятности в независимых испытаниях.
- •Вопрос 8. Дискретные случайные величины (дсв). Закон распределения вероятностей дсв. Многоугольник распределения. Функция распределения дсв. Основные законы распределения дсв (6 законов).
- •Вопрос 9. Числовые характеристики дсв. Основные законы распределения дсв. Числовые характеристики для основных законов.
- •Вопрос 12. Числовые характеристики нсв.
- •Вопрос 13. Равномерный закон распределения нсв. Интегральная и дифференциальная функции и их графики. Числовые характеристики. Вероятность попадания в заданный интервал.
- •Вопрос 14. Показательный закон распределения нсв. Интегральная и дифференциальная функции и их графики. Числовые характеристики. Вероятность попадания в заданный интервал.
- •Вопрос 16. Закон распределения функции от случайной величины. Нахождение плотности вероятности, математического ожидания, дисперсии.
- •Вопрос 17. Система двух случайных величин. Закон распределения двумерной дсв. Законы распределения составляющих. Условные законы распределения составляющих двумерной дсв.
- •Вопрос 18. Двумерная нсв. Интегральная функция. Дифференциальная функция и условная дифференциальная функция. Вероятность попадания в область.
- •Вопрос 20. Специальные законы распределения.Χ2 - распределение Пирсона. T – распределение Стьюдента. F – распределение Фишера-Снекедора.
Вопрос 1. Событие. Пространство элементарных событий. Достоверное событие, невозможное событие. Совместные, несовместные события. Равновозможные события. Полная группа событий. Операции над событиями. Алгебра событий.
Под
событием в теории вероятности понимается
всякий факт, который в результате опыта
может произойти или не произойти.
Простейшие неразложимые результаты
опыта, называются элементарными
событиями. Вся совокупность элементарных
событий образует пространство
элементарных событий. Событие – любое
конечное (счетное) подмножество
пространства элементарных событий.
Достоверное А=Ω, невозможное А=0= .
События А и В называются несовместными,
если в результате одного опыта они не
могут произойти одновременно. В противном
случае эти события совместны.
Равновозможными называются события,
если ни одно из них не имеет объективного
преимущества перед другими. Несколько
событий в одном опыте образуют полную
группу событий, если в результате опыта
непременно должно появиться хотя бы
одно из них.
.
События А и В называются несовместными,
если в результате одного опыта они не
могут произойти одновременно. В противном
случае эти события совместны.
Равновозможными называются события,
если ни одно из них не имеет объективного
преимущества перед другими. Несколько
событий в одном опыте образуют полную
группу событий, если в результате опыта
непременно должно появиться хотя бы
одно из них.
А+В=А
 В
ВА*В=А В
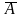 =
–А
=
–АА-В=А\В
= Ω\А
Множество σ называется алгеброй событий, если σ множество всех подмножеств множества ω, для которых выполняется следующие условия:
А, В σ
 А+В
σ
А+В
σА, В σ А*В σ
А σ σ
Вопрос 2. Аксиоматическое определение вероятности. Классическое, статистическое, геометрическое определение вероятности события.
Аксиоматическое
определение вероятности. Пусть задано
пространство элементарных событий
Е и каждому событию А
![]() Е
поставлено в соответствие
единственное число Р ( А ) такое,
что:
Е
поставлено в соответствие
единственное число Р ( А ) такое,
что:

Тогда говорят, что на событиях в множестве Е задана вероятность, а число Р ( А ) называется вероятностью события А .
Классическое определение вероятности. Пусть пространство элементарных событий Е состоит из N равновозможных элементарных событий, среди которых имеется n событий, благоприятствующих событию А , тогда число Р ( А ) = n / m называется вероятностью события А .
Статистическое
определение вероятности. Пусть
производится серия опытов (n),
в результате которых событие А наступает
m раз число
 - частота наступления события А, тогда
под вероятностью события А будем
понимать предел при Р(А)=
- частота наступления события А, тогда
под вероятностью события А будем
понимать предел при Р(А)=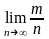
Геометрическое
определение вероятности. Пусть в
области G наудачу бросается
точка, какова вероятность попадания
точки в область g, лежащей
в области G. По определению
вероятность такого события Р(А)=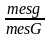 .
.
Вопрос 3. Свойства вероятности. Теоремы сложения и умножения вероятностей. Независимые события. Условная вероятность. Вероятность наступления хотя бы одного из событий.
1.
 ;
;
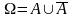 ,
,
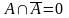 ,
по аксиоме сложения
,
по аксиоме сложения
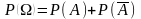 ,
по аксиоме
,
по аксиоме

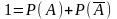
2.Р(Ø)=0; Ω= Ω Ø, Ω Ø=Ø по аксиоме сложения Р(Ω)= Р(Ω)+ Р(Ø) Р(Ø)=0
3.А
В,
если событие А влечет за собой событие
В, то вероятность события А:Р(А) Р(В);
А=А
(В\А),
А
(А
(В\А))=0
по аксиоме сложения
Р(А)=Р(А)+Р(В\А)
Р(В\А)=0
Р(А)
Р(В)
Р(В);
А=А
(В\А),
А
(А
(В\А))=0
по аксиоме сложения
Р(А)=Р(А)+Р(В\А)
Р(В\А)=0
Р(А)
Р(В)
4. 0 Р(А) 1
5.
6. А=В+С, В*С=0, Р(А)=Р(В)+Р(С)
Теорема сложения. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий Р(А+В)=Р(А)+Р(В). Предположим, что m случаев благоприятны событию А, а k событию В, тогда Р(А)=m\n; Р(В)=k\n. Так как события А и В несовместны, то нет таких случаев, которые благоприятны А и В вместе. Следовательно, событию А+В благоприятны m+k случаев и Р(А+В)=( m+k)\n
Теорема умножения. Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии что первое имело место. Р(АВ)=Р(А)Р(В\А). предположим что событию А благоприятны m случаев, а В – k. Т.к.мы не предполагали события А и В несовместными, то вообще существуют случаи, благоприятные и для А и для В одновременно. Пусть число таких случаев l, тогда Р(АВ)=l\n, Р(А)=m\n. Р(В\А) – условная в-ть события, в предположении что А имело место. Если известно что событие А произошло, то из ранее возможных n случаев остаются возможными только те m,которые благоприятствовали событию А. из них l случаев благоприятны событию В, следовательно Р(А\В)=l\m
Вопрос 4. Формула полной вероятности. Формула Байеса (вероятности гипотез).
Предположим,
что событие В может произойти с одним
и только с одним из n
несовместных событий А1, А2, …, Аn,
образующих полную группу событий
(Р(А1)+Р(А2)+…+Р(Аn)=1), т.е.
В=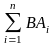 ,
ВАi и ВАj
несовместны при i≠j
по
т. Сложения Р(В)=
,
ВАi и ВАj
несовместны при i≠j
по
т. Сложения Р(В)= ,
а по т. умножения Р(В)=
,
а по т. умножения Р(В)=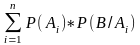 - формула полной вероятности.
- формула полной вероятности.
Пусть произошло событие В; А1, А2, …, Аn – гипотезы. Найдем вероятность гипотезы Р(Аi) при условии, что событие В произошло.
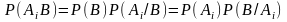 ;
;
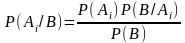 .
Используя формулу полной вероятности
получим
.
Используя формулу полной вероятности
получим
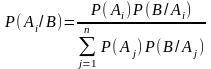 - формула Байеса.
- формула Байеса.
