- •Вопрос 2. Аксиоматическое определение вероятности. Классическое, статистическое, геометрическое определение вероятности события.
- •Вопрос 3. Свойства вероятности. Теоремы сложения и умножения вероятностей. Независимые события. Условная вероятность. Вероятность наступления хотя бы одного из событий.
- •Вопрос 4. Формула полной вероятности. Формула Байеса (вероятности гипотез).
- •Вопрос 5. Повторные независимые испытания. Формула Бернулли. Полиномиальная формула. Наивероятнейшее число появлений события в независимых испытаниях.
- •Вопрос 7. Применение интегральной теоремы Муавра-Лапласса. Отклонение относительной частоты от постоянной вероятности в независимых испытаниях.
- •Вопрос 8. Дискретные случайные величины (дсв). Закон распределения вероятностей дсв. Многоугольник распределения. Функция распределения дсв. Основные законы распределения дсв (6 законов).
- •Вопрос 9. Числовые характеристики дсв. Основные законы распределения дсв. Числовые характеристики для основных законов.
- •Вопрос 12. Числовые характеристики нсв.
- •Вопрос 13. Равномерный закон распределения нсв. Интегральная и дифференциальная функции и их графики. Числовые характеристики. Вероятность попадания в заданный интервал.
- •Вопрос 14. Показательный закон распределения нсв. Интегральная и дифференциальная функции и их графики. Числовые характеристики. Вероятность попадания в заданный интервал.
- •Вопрос 16. Закон распределения функции от случайной величины. Нахождение плотности вероятности, математического ожидания, дисперсии.
- •Вопрос 17. Система двух случайных величин. Закон распределения двумерной дсв. Законы распределения составляющих. Условные законы распределения составляющих двумерной дсв.
- •Вопрос 18. Двумерная нсв. Интегральная функция. Дифференциальная функция и условная дифференциальная функция. Вероятность попадания в область.
- •Вопрос 20. Специальные законы распределения.Χ2 - распределение Пирсона. T – распределение Стьюдента. F – распределение Фишера-Снекедора.
Вопрос 7. Применение интегральной теоремы Муавра-Лапласса. Отклонение относительной частоты от постоянной вероятности в независимых испытаниях.
Оценим
вероятность неравенства
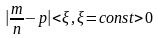 (*),
(*),
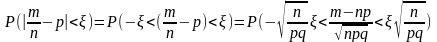 ,
закон больших чисел или т. Бернулли
,
закон больших чисел или т. Бернулли
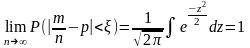 ,
для любого ξ вероятность неравенства
(*) стремится к 1. Найти вероятность того,
что частота события А отклонится от ее
вероятности не более чем на α, n-независимые
испытания, вероятность p,
q=1-p,
,
для любого ξ вероятность неравенства
(*) стремится к 1. Найти вероятность того,
что частота события А отклонится от ее
вероятности не более чем на α, n-независимые
испытания, вероятность p,
q=1-p,
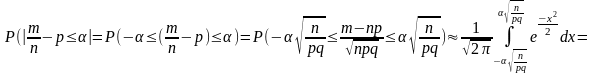
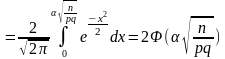 .
Какое наименьшее число испытаний нужно
произвести, чтобы с вероятностью не
меньше чем β частота отклонялась от
вероятности наступления события не
больше чем на α, n=?,
.
Какое наименьшее число испытаний нужно
произвести, чтобы с вероятностью не
меньше чем β частота отклонялась от
вероятности наступления события не
больше чем на α, n=?,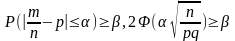 .
По данной вероятности β числу испытаний
n определить границу
отклонения частоты от вероятности
наступления события
.
По данной вероятности β числу испытаний
n определить границу
отклонения частоты от вероятности
наступления события
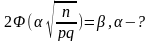
Вопрос 8. Дискретные случайные величины (дсв). Закон распределения вероятностей дсв. Многоугольник распределения. Функция распределения дсв. Основные законы распределения дсв (6 законов).
Случайная величина (СВ) – действительная функция, определенная на пространстве элементарных событий (Ω). ДСВ – принимает конечное или бесконечное счетное число значений. Законом распределения ДСВ называют соответствие между значением СВ и вероятностями, с которыми она принимает эти значения, причем рассматриваются все возможные значения этой величины, записывают в виде таблиц
Х |
х1 |
х2 |
… |
хn |
Р |
p1 |
p2 |
… |
pn |
х1<x2<…<xn, т.к. это все возможные знач. ДСВ(Х), то соб. Х=х1, Х=х2…Х=хn, то соб. образ. полную группу (сис-му). р1+р2+…+рn=1 эта формула применяется для контроля правильности построения закона распределения ∑Pn=1.
Возьмем прямоугольную систему координат. По оси х отложим значения СВ Х, а по оси у- вероятность этих значений. Соседние точки (хi,pi) cоединим отрезками, тогда получим фигуру, которая называется полигоном (многоугольником) распределения СВ.
Если
![]() -
случайная величина, то функция
-
случайная величина, то функция
![]()
называется функцией распределения
случайной величины
.
Здесь
![]() -
вероятность того, что случайная величина
принимает
значения, не превосходящие числа
-
вероятность того, что случайная величина
принимает
значения, не превосходящие числа
![]() .
.
Функция распределения любой случайной величины обладает следующими свойствами:
определена на всей числовой прямой
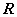 ;
;
не убывает, т.е. если
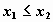 ,
то
,
то
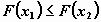 ;
;
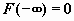 ,
,
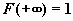 ,
т.е.
,
т.е.
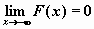 и
и
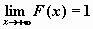 ;
;
непрерывна справа, т.е.
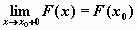 .
.
Функция распределения содержит всю информацию об этой случайной величине и поэтому изучение случайной величины заключается в исследовании ее функции распределения, которую часто называют просто распределением. Так что, когда говорят о нормальном распределении, то подразумевают случайную величину, имеющую нормальную функцию распределения.
У дискретной случайной величины функция распределения ступенчатая.
Закон
распределения Бернулли. Случайная
величина
![]() ,
распределенная по закону Бернулли,
принимает значения: 1 – «успех» или 0 –
«неудача» с вероятностями p
и q=1-p
соответственно
,
распределенная по закону Бернулли,
принимает значения: 1 – «успех» или 0 –
«неудача» с вероятностями p
и q=1-p
соответственно
xi |
0 |
1 |
pi |
q |
p |
Математическое ожидание: СВ X: M(X)=0*q+1*p=p.
Дисперсия: D(X)=02*q+12*p-p2=p(1-p).
Биномиальный закон распределения. Случайная величина , распределенная по биномиальному закону, принимает значения:
0, 1, 2, …, n с вероятностями, определяемыми по формулам Бернулли:
![]()
xi |
0 |
1 |
2 |
,,, |
|
,,, |
|
pi |
|
|
|
|
|
|
|
Математическое ожидание: M(X)=np.
Дисперсия: D(X)=npq.
Закон
распределения Пуассона. Случайная
величина
,
распределенная по закону Пуассона,
принимает бесконечное счетное число
значений: 0, 1, 2, …, k, …, с
соответствующими вероятностями,
определяемыми по формуле Пуассона
![]() ,где
,где
![]() – параметр распределения Пуассона.
– параметр распределения Пуассона.
При
![]() и
и
![]() биномиальный закон распределения
приближается к закону распределения
Пуассона, где
биномиальный закон распределения
приближается к закону распределения
Пуассона, где
![]() .
.
Математическое
ожидание
![]() .
.
Дисперсия
![]() .
.
Геометрическое распределение. Дискретная случайная величина X имеет геометрическое распределение, если она принимает значения 1, 2, ..., m, ... (бесконечное, но счётное множество значений) с вероятностями
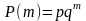
где 0 < p < 1, q=1 - p, m =1, 2, ...
Ряд геометрического распределения имеет вид:
xi |
1 |
2 |
3 |
... |
m |
... |
pi |
p |
pq |
pq2 |
... |
pqm-1 |
... |
Случайная величина X=m, имеющая геометрическое распределение, представляет собой число m испытаний, проведённых по схеме Бернулли, с вероятностью p наступления события в каждом испытании до первого положительного исхода.
Математическое
ожидание СВ X, имеющей геометрическое
распределение с параметром p,
![]() ,
дисперсия
,
дисперсия
![]() ,
где q= 1-p.
,
где q= 1-p.
Отрицательное
биномиальное распределение.
Производится ряд независимых опытов,
в каждом из которых событие А появляется
с вероятностью р до получения k
успехов. Случайная величина Х –
количество неудачных опытов, m=0,1,…,
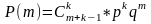
Гипергеометрический
закон. Схема урн. В урне N
шаров, M - белых, n
шаров вытянули, СВ Х – количество белых
шаров среди вытянутых
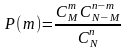
xi |
0 |
1 |
… |
m |
pi |
|
|
|
|