Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный университет экономики, статистики и информатики (МЭСИ)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

41_2_Econometrics_Polyansky__Part_2

.pdf

Скачиваний:

Добавлен:

05.06.2015

Размер:

1.55 Mб

Скачать

☆

1 / 21 2 > Следующая >>>

Полянский Ю.Н.

Эконометрика. Экономическое моделирование и прогнозирование.

ГЛАВА 2. ПАРНАЯ НЕЛИНЕЙНАЯ РЕГРЕССИЯ

2.1. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

На практике между экономическими показателями часто наблюдаются более сложные – нелинейные – регрессионные зависимости.

2.1.1. Основные типы нелинейных регрессий

полиномиальные:

квадратичные y ax

c (рис.2.1-а),

кубические

y ax

cx d

(рис. 2.1-б) и т. д.;

гиперболическая

y a

(рис.2.1-в);

степенная y a

(рис.2.1-г);

показательная y a b

(рис.2.1-д), в т.ч. экспоненциальная

y e

a bx

(см.:

y e

( e

)

a1 b1

1 ).

логарифмическая

y a b ln x (рис. 2.1-е).

Кроме указанных нелинейных регрессий, возможно использование в экономической практике других, в том числе и получающихся из вышеперечисленных путём математических преобразований, например:

y a

ln y a

1 bx

	;

;

y	2
ax

ln ˆy ax 2

1 bx

	;

Могут применяться различные комбинации указанных зависимостей, а также использоваться другие, не указанные здесь. Широкое применение в экономике и социологии получили так называемые кривые с насыщением, выходящие на асимптоту при достижении определенных значений показателей. Например, при анализе временных рядов в страховом деле, банковском деле, демографии часто используется кривая Гомперца, существенно изменяющая свой вид при различных значениях параметров (рис.2.2):

где

y K a bt ,

K , a , b - параметры; t - время (1, 2, …).

Находит применение и логистическая кривая (рис.2.3)

y		K

		be at
1

Полянский Ю.Н. Эконометрика. Экономическое моделирование и прогнозирование.

а) квадратичная

б) кубическая

в) гиперболическая

г) степенная

д) показательная е) логарифмическая

Рис. 2.1. Примеры нелинейных регрессий.

Полянский Ю.Н.

Эконометрика. Экономическое моделирование

а) при logс a 0, b 1 (с>1)

в) при logс

a 0

, b 1

(с>1)

Рис. 2.2. Кривая Гомперца	y K

и прогнозирование.

б) при logс

a 0

, b 1

(с>1)

		г) при logс	a 0, b 1	(с>1)
a	b	t
	b	при различных значениях параметров.

Рис. 2.3. Логистическая кривая	y	K	.

		be at
	1

Полянский Ю.Н. Эконометрика. Экономическое моделирование и прогнозирование.

В подобных функциях параметр K определяется как максимум функции, а в дальнейшем параметры a и b определяются методом наименьших квадратов.

В парной регрессии выбор вида функции может осуществляться сле-

дующими методами:

аналитическим;

графическим;

экспериментальным.

На практике необходимо по возможности использовать наиболее простые зависимости. Попытка получить некую «универсальную» регрессию для всего изучаемого диапазона объясняющей переменной может привести к снижению точности модели.

Для повышения точности и упрощения модели возможно разделение диапазона x на несколько участков, каждый со своими коэффициентами уравнения регрессии или даже своей спецификацией модели.

2.1.2. МНК для парной квадратичной модели

y = ax	2	+ bx + c + ε

Потребуем

F ( a ,b,c ) ( yi i 1

( ax	2	bx
	i		i

c ))2

min

Без подробного вывода приведем здесь итоговую систему линейных алгебраических уравнений (СЛАУ) для расчета коэффициентов регрессии:

		n
		a x
		i 1
		i 1
		n

	a x
		i 1
		n

	a x
		i 1

4 i

3 i

2 i

nb x

i 1

nb x

i 1

nb x

i 1

	n	n
3	2		2	yi	,
i	c xi	xi		yi	,
	i 1	i 1
	n	n
2	c xi	xi		yi	,
i	c xi	xi		yi	,
	i 1	i 1
		n
i	c n		yi .
		i 1

(2.1)

Получение готовых формул для коэффициентов регрессии в этом случае затруднительно. Однако система может быть достаточно просто решена с помощью любого метода решения СЛАУ (Гаусса, Крамера, обратной матрицы, подстановки и др.). Определим коэффициенты СЛАУ (например, с помощью функции MS Excel СУММ) и обозначим их:

S20

S30

S40 xi

xi ,

i 1

x2 y

, S

i 1

Тогда СЛАУ в матричном виде выглядит: AX

		n
S	10	x
	10	i 1
		i 1
yi , S00

n .

Полянский Ю.Н.

Эконометрика. Экономическое моделирование и прогнозирование.

где A S

S20

S10

X b ,

B S11

S10

S01

S20

S00

Например, методом Крамера (методом определителей) [14] решение может осуществляться с помощью встроенной в Microsoft Excel функции МОПРЕД (вычисление определителя матрицы) по следующим формулам:

S40 S30 где A S30 S20

S20 S10

		1

S20

S10

S00

b	2	,

1 A1

c
	3	,		(2.2)
		,		(2.2)

S21		S30	S20
S11		S20	S10	,
S01		S10	S00

(2.3)

		S	40	S	21	S	20
			40		21		20
2	A	S	30	S	11	S	10
2	2		30		11		10
		S	20	S	01	S	00
			20		01		00

		S	40	S	30	S	21
			40		30		21
3	A	S	30	S	20	S	11
3	3		30		20		11
		S	20	S	10	S	01
			20		10		01

2.1.3. Линеаризация некоторых нелинейных регрессий

Некоторые нелинейные регрессии путем математических преобразований могут быть сведены к соответствующим линейным регрессиям относительно других (производных) переменных. Параметры полученных линеаризованных моделей можно найти описанными выше методами.

а) Показательная модель

y a bx

Прологарифмируем левую и правую части уравнения и преобразуем полученное равенство:

ln y ln( a b	x	) ln a ln b	x	ln

Введем промежуточные переменные
ln y Y		; ln a A ;	lnb B ;

ln a x ln b ln

ln E .

С учетом введенных обозначений имеем парную линейную регрессию

Y A Bx E .

Её отличие от исходной в том, что в качестве объясняемой переменной выступает не исходная y , а Y ln y . Т.е. в расчетах необходимо брать

не исходный массив объясняемой переменной y , а массив предварительно

полученных ее логарифмов. Но и получены в результате расчетов будут не коэффициенты a и b , а их логарифмы ln a A и lnb B . Из них требуе-

Полянский Ю.Н. Эконометрика. Экономическое моделирование и прогнозирование.

мые значения можно получить:

a e	ln a	e	A	,	b e	ln b	e	B	.
	ln a		A			ln b		B

Остается только подставить полученные значения коэффициентов в уравнение исходной парной нелинейной регрессии y a bx .

б) Гиперболическая модель

Обозначим	1	x	X .

y a b	x
	x

С учетом введенных обозначений имеем парную линейную регрессию

y a bX

Для расчетов необходимо указать предварительно полученный массив данных, обратных объясняющей переменной. И сразу будут получены готовые коэффициенты a и b .

в) Квадратичная модель

y ax	2

bx c

Она также может быть линеаризована и сведена к линейной множественной (конкретно - к двухфакторной) модели.

Введём промежуточные переменные x1	x	2	, x2	x .

Тогда имеем множественную линейную регрессию

y ax	1	bx	2	c	.

Вычисления её коэффициентов производится, как и у всех множественных линейных регрессий (см. далее раздел 3).

!Замечание.

Обратите внимание, что число оцениваемых параметров для квадратичной

модели m = 3 ( x1 , x2 и		y ), а не 2, как у линейной, степенной и т.п. (
Для кубической модели	y ax		3	bx	2	cx d	m = 4 .

Аналогично могут быть линеаризованы и другие нелинейные регрессии (например, см. задачи ниже).

2.1.4. Характеристики парных нелинейных регрессий

Оценкой тесноты нелинейной связи служит индекс корреляции


			n
		1	( yi	ˆyi )2	(2.4)
R		1	n		(2.4)
	2		i 1
			( yi y )2
			i 1

Описанные выше в разделе 1 коэффициент детерминации R2 (1.4) и

Полянский Ю.Н.

Эконометрика. Экономическое моделирование и прогнозирование.

средняя относительная ошибка A (1.6) характеризуют качество не только линейного, но и нелинейного уравнения регрессии. Силу связи переменных в нелинейной (как и в линейной) регрессии характеризует средний коэффи-

циент эластичности Э (1.7).

!Замечания.

Часто при линеаризации получаются не самые лучшие нелинейные регрессии даже при использовании метода наименьших квадратов. Дело в том, что в линеаризованной модели на самом деле используется не стандартное требование

МНК

(ln yi i 1

n
( yi				ˆyi )2 min,	а	несколько	другие	(например
i 1				min). Иногда это может привести просто к абсурдному (с
ln ˆy		)	2	min). Иногда это может привести просто к абсурдному (с
			2
	i

точки зрения исследователя) результату.

Неверно оценивать качество и значимость нелинейной модели по характеристикам промежуточной линеаризованной модели. Полученные для линеаризованной модели показатели (например, коэффициент детерминации) использовать для оценки некорректно. Оценивать необходимо исходную модель, её прогнозные значения и показатели. К сожалению, Пакет анализа не позволяет явно

вычислять	R	2	для нелинейных регрессий, а лишь предоставляет возможность

увидеть его приближенное (до 4 знака после запятой) значение, используя средство «Вставка линии тренда» (см. задачу 2.3).

2.2. ПРАКТИЧЕСКИЕ ЗАДАНИЯ

Задача 2.1

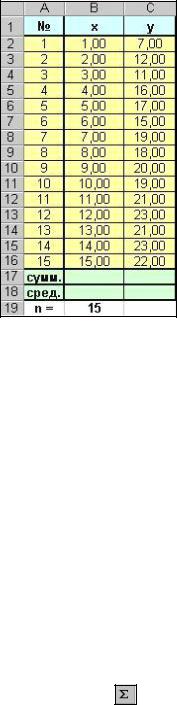
Пользуясь приведенными на рис.2.4 исходными данными об объемах производства пластиковых окон некоторой фирмой (Y, млн. $) в течение первых n=15 лет её существования (X, годы):

1)получить уравнение парной нелинейной квадратичной регрессии Y

на X

y ax	2

bx c

;

2)оценить тесноту нелинейной связи переменных с помощью индекса корреляции ;

3)оценить качество подгонки квадратичного уравнения индексом детерминации R 2 ;

4)оценить качество модели с помощью средней относительной ошибки

5)аналогичные y a bx

расчеты выполнить для линейной модели

;

6)результаты совместить на одном графике; сделать вывод, какая из этих двух моделей предпочтительнее.

Полянский Ю.Н. Эконометрика. Экономическое моделирование и прогнозирование.

Решение.

В документе Microsoft Excel заготовим

расчетную таблицу (рис.2.4).
Нанесем	исходные	данные

(эксперимент) на график для их визуальной оценки (см. далее рис.2.7).

По общему виду точечного графика делаем предварительный вывод о наличии нелинейности в регрессионной зависимости наблюдаемых значений объясняемой переменной Y от объясняющей переменной X. Попробуем в качестве нелинейной регрессии парную квадратичную регрессию

y ax	2

bx c

Рис. 2.4

1) По приведенным исходным данным определим оценки коэффициентов квадратичной регрессии. Применение к ней метода наименьших квадратов приводит к следующей системе линейных

(относительно искомых	aˆ	,	ˆ
			b , cˆ )

суммирования записаны упрощенно):

алгебраических уравнений (символы

aˆ

b x

cˆ

aˆ

ˆy

b x

aˆ

cˆ

ˆy

b x

Решим её относительно неизвестных коэффициентов

aˆ

, b , cˆ любым

доступным методом, например, методом Крамера. Входящие в систему суммы являются коэффициентами при неизвестных. Введём в расчетную таблицу дополнительные столбцы D, E, F, G, H, подписав их соответственно

смыслу вычислений, и вычислим в них текущие значения x 4 , x 3 ,	x 2 , x 2 ˆy ,
ˆ
xy для каждого i-го наблюдения. Соответствующие суммы вычислим в
расчетной таблице с помощью функции СУММ (кнопки	панели
инструментов) в 17-й строке Microsoft Excel (рис.2.5).

Сформируем матрицу A системы, состоящую из коэффициентов при неизвестных в левых частях уравнений. Подпишем её «А=» в ячейке A22. Желательно также выделить место под матрицу B21:D23 цветом и/или рамкой. Т.к. в верхнем левом углу (элемент a11 ) решаемой системы

уравнений стоит коэффициент, представляющий сумму x	4	, то напишем в

ячейке B21 формулу-ссылку «=F17». Остальные ячейки матрицы заполним формулами-ссылками на графы расчетной таблицы, соответствующие коэффициентам системы уравнений (рис.2.5).

Полянский Ю.Н.

Эконометрика. Экономическое моделирование и прогнозирование.

Рис. 2.5

В соответствии с алгоритмом метода Крамера наберём матрицу A1 ,

подобную только что полученной матрице A , в которой вместо элементов первого столбца должны размещаться элементы правых частей уравнений системы. Это удобно и быстро сделать следующим образом. Подписав ячейку A26 комментарием «A1=», в верхнем левом углу набираемой матрицы (в ячейке B25) напишем формулу-ссылку на ячейку B21 матрицы A . Протянем ячейку B25 сначала по строке B25:D25, а затем эту

выделенную строку вниз по строкам B25:D27. Получим копию матрицы				A .
Теперь просто подправим 1-й		столбец матрицы	A1 ссылками	на
ячейки H17, G17 и С17, соответствующие правым частям СЛАУ.
Аналогично набираются и матрицы A2		и A3 , в которых соответственно 2-й
и 3-й столбцы состоят из коэффициентов правых частей уравнений.
По алгоритму метода Крамера необходимо вычислить значения
определителей (детерминантов) , 1 , 2 , 3 полученных матриц.				Их
получим с помощью функции МОПРЕД в ячейках J21:K24.
Расчет коэффициентов уравнения по формулам Крамера удобно
произвести в ячейках напротив		соответствующих	определителей.
Вычисления коэффициентов: aˆ				ˆ
	(в ячейке M22) - по формуле «=K22/K21», b
(в ячейке M23) - «=K23/K21», cˆ	(в ячейке M24) - «=K24/K21».

В итоге получаем уравнение парной квадратичной регрессии:

ˆy 0,074x 2 2,151x 6,523.

Полянский Ю.Н. Эконометрика. Экономическое моделирование и прогнозирование.

2) Оценим тесноту нелинейной связи индексом корреляции

	n
	( yi	yˆ i	)		2
1	( yi	yˆ i	)
1	n
	i 1
	( yi	y)		2
	( yi	y)
	i 1

Для его вычисления необходимы оценочные значения объясняемой переменной Y для каждого i-го наблюдения. Это выполним в столбце J, подписав его «y*». Запрограммируем в ячейке J2 формулу полученной выше квадратичной регрессии «=$M$22*B2*B2+$M$23*B2+$M$24», которую протянем по диапазону J2: J16.

!Замечание.

Расчет нельзя проводить с помощью Пакета анализа или функций ПРЕДСКАЗ, НАКЛОН, ОТРЕЗОК, т.к. они рассчитывают параметры линейной регрессии.

Дальнейшие вычисления сумм

n	2
ˆ	2
( yi yi )
i 1

и	n		i
и		( y	i	y )	2
					2

	i 1

проведём

в столбцах K и L. Искомые суммы получим в ячейках K17 и L17 (рис.2.5). Вычисление индекса корреляции проведём в ячейке K25, запрограм-

мировав формулу «=КОРЕНЬ(1-(K17/L17))». Полученное значение индекса корреляции 0,959 свидетельствует о наличии очень тесной нелиней-

ной связи между X и Y.

Полученные выше оценочные значения

yˆ

нанесем на общий график с

наблюдаемыми значениями

(см. далее рис. 2.7).

3) Оценим качество подгонки полученного квадратичного уравнения

регрессии с помощью коэффициента детерминации

R	2

!Замечание.

Коэффициент детерминации оценивает качество подгонки как линейной регрессии, так и нелинейной. Для нелинейной регрессии его часто называют индексом де-

терминации.

Фактически индекс детерминации – квадрат индекса корреляции. Поэтому рассчитываем его в ячейке K26 по формуле «=K25*K25» (рис.2.5).

Результат

R	2	0 ,920

близок к 1, что свидетельствует о достаточно высоком

качестве подгонки полученного выше квадратичного уравнения регрессии. 1) Оценим точность модели средней относительной ошибкой

	1	n		1	n
A			i
A	n		A	n
	n	i 1		n	i 1

y	i


y	i

ˆy	i

100%

Расчеты выполним в столбце M, запрограммировав в ячейке M2 формулу «=ABS((C2-J2)/C2)» и протянув её по диапазону ячеек M2:M16. Зададим

процентный формат ячеек M2:M18 (меню «Формат/Ячейки» или кнопкой ). Полученные текущие значения относительных ошибок Ai осредним в ячейке

1 / 21 2 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.11.201934.63 Кб104.docx
#
27.10.2018153.39 Кб740-50_билеты.docx
#
14.04.2019818.44 Кб13401196_C9AEF_voprosy_k_ekzamenu_po_teorii_veroy....docx
#
05.06.2015279.58 Кб4841_0_Econometrics_Polyansky__Part_0.pdf
#
05.06.20151.7 Mб3441_1_Econometrics_Polyansky__Part_1.pdf
#
05.06.20151.55 Mб2741_2_Econometrics_Polyansky__Part_2.pdf
#
05.06.20151.08 Mб2741_3_Econometrics_Polyansky__Part_3.pdf
#
05.06.20151.44 Mб2541_4_Econometrics_Polyansky__Part_4.pdf
#
05.06.20151.45 Mб2341_5_Econometrics_Polyansky__Part_5.pdf
#
05.06.2015676.83 Кб2341_6_Econometrics_Polyansky__Part_6.pdf
#
05.06.20153.64 Mб4441_7_Econometrics_Polyansky__Additions.pdf