3.7. Основные достоинства метода дп

1. Идея и метод ДП наиболее приспособлены к дискретным задачам, каковыми являются задачи из экономики.

2. Метод ДП применим при любом способе задания F_ц и любом допустимом множестве состояний и управлений. Этого преимущества лишены классические методы оптимизации и другие вычислительные методы математического программирования.

3. Вычислительные схемы метода ДП в дискретном случае связаны с перебором оптимальных значений показателя эффективности и управления на k-м шаге для всех возможных значений переменной состояния, но объем расчетов по этому методу значительно меньше, чем при прямом переборе вариантов. Это связано с тем, что на этапе условной оптимизации неудачные варианты сразу отбрасываются, а сохраняются лишь условно оптимальные на данном шаге.

4. Метод ДП дает возможность анализа чувствительности к изменению исходных данных S_k и n. Фактически здесь решается не одна задача, а множество однотипных задач для различных состояний S_k и различных k (1  k  n) на каждом шаге. Поэтому при изменении исходных данных можно не решать задачу заново, а сделать лишь несложные добавления к уже выполненным расчетам, т.е. продолжить уже решенную задачу за счет увеличения числа шагов n или числа значений S_k.

3.8. Типовые задачи в моделях дп

Задача 1. Задача маршрутизации.

Задача маршрутизации является основной задачей индексного метода в теории графов и ставится для произвольного орграфа без контуров. Модель ДП для этой задачи демонстрирует связь ИМ и ДП.

1. Особенностью модели ДП для задачи маршрутизации является отсутствие уравнения состояний (1), так как роль переменных состояния S_k и роль переменных управления u_k выполняют попеременно одни и те же вершины графа, т.е. или a_k = S_k, или a_k = u_k.

Рассмотрим, что происходит при условной оптимизации, учитывая, что при прямом ходе управлением являются левые вершины дуг, а при обратном – правые.

При прямом ходе проходятся следующие дуги:

–на k-м шаге: (a_k–1, a_k)  (a_k = S_k);

–на (k+1)-м шаге: (a_k, a_k+1)  (a_k = u_k).

При обратном ходе проходятся дуги:

–на (k+1)-м шаге: (a_k, a_k+1)  (a_k = S_k);

– на k-м шаге: (a_k–1, a_k)  (a_k = u_k).

Теперь рассмотрим, что происходит при безусловной оптимизации, когда для поиска решения задачи (т.е. оптимального маршрута) используется уравнение состояний. Итак, при обратном ходе имеем цепочку:

(S₀  u₁  S₁  u₂  S₂  …  u_n  S_n)

или

(a₀  a₁  a₁  a₂  a₂  …  a_n  a_n),

или

(a₀  a₁  a₂  …  a_n),

что является решением задачи. Переходы (u_k  S_k) пропадают и надобность в уравнении (1) отпадает. Остаются только переходы (S_k–1  u_k) или дуги (a_k–1, a_k), связывающие два соседних уровня E_k–1 и E_k. Аналогично происходит и при прямом ходе. Следовательно, роль уравнения состояний выполняют дуги уровней (E_i–1, E_i) при обратном ходе и дуги уровней (E_i, E_i+1) при прямом.

2. Показателем эффективности k-го шага являются веса дуг v_k(a_k–1, a_k), т.е. стоимости перехода от E_k–1 к E_k. Тогда суммарный показатель эффективности

(тип 2)

где F – целевая функция.

Задача теперь формулируется стандартно: требуется найти последовательность вершин a₀, a₁,…, a_n, переводящую систему из a₀ в a_n, и оптимизирующих F, т.е. приводящих Z к оптимуму (см. общую постановку задачи ДП).

3. Критерий эффективности k-го шага.

Вводится суммарный показатель эффективности за первые k шагов для прямого хода:

или за последние (n – k) шагов для обратного хода:

4. Теперь функциональные уравнения Беллмана можно записать в следующем виде.

В общем случае:

– для обратного хода:

так как (тип 3)

(тип 4)

при этом opt Z = Z₀(S₀);

– для прямого хода:

так как (тип 3')

(тип 4')

при этом opt Z = Z_n(S_n).

При последовательном графе:

– для обратного хода:

так как (тип 3)

(тип 4)

при этом opt Z = Z₀(S₀);

– для прямого хода:

так как (тип 3')

(тип 4')

при этом opt Z = Z_n(S_n).

5. Безусловная оптимизация проводится упрощенно по последовательности условных оптимальных управлений {u_k(S_k)}. Результатом ее является последовательность вершин с условными оптимумами {Z_k(S_k)}:

(a₀  a₁  …  a_n–1  a_n) – для обратного хода и

(a_n  a_n–1  …  a₁  a₀) – для прямого хода.

Связь с индексным методом очевидна:

6. Иллюстративный пример. Пусть задан последовательный орграф без контуров с весами v_k(a_k–1, a_k) на дугах (рис. 3.1).

Поскольку граф последовательный, то на множестве его вершин заведомо задана порядковая функция.

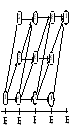
Веса на дугах v_k(a_k–1, a_k) зададим списком:

v1 (1, 2) = 10	v2(2, 5) = 3	v3(5, 8) = 2	v4(8, 11) = 2
v1 (1, 3) = 8	v2(3, 5) = 6	v3(6, 8) = 3	v4(9, 11) = 5
v1 (1, 4) = 5	v2(4, 5) = 9	v3(7, 8) = 4	v4(10, 11) = 6
	v2(3, 6) = 3	v3(6, 9) = 2
	v2(4, 6) = 6	v3(7, 9) = 3
	v2(4, 7) = 3	v3(7, 10) = 2

Требуется найти путь S(1, 11) при условии Z = min. Воспользуемся прямым ходом, т.е. будем двигаться от E₀ к E₄, последовательно выписывая и решая функциональные уравнения

Z₀(a₀) = Z₀(1)  0 (по построению).

Z₁(a₁) = Z₀(1) + v₁(1, a₁) = 0 + v₁(1, a₁),

тогда

Z₁(2) = v₁(1, 2) = 10, a₀ = 1;

Z₁(3) = v₁(1, 3) = 8, a₀ = 1;

Z₁(4) = v₁(1, 4) = 5, a₀ = 1.

тогда

= min (10 + 3, 8 + 6, 5 + 9) = 13, a₁ = 2;

= min (8 + 3, 5 + 6) = 11, a₁ = 3, 4;

тогда

= min (13 + 2, 11 + 3, 8 + 4) = 12, a₂ = 7;

= min (11 + 2, 8 + 3) = 11, a₂ = 7;

тогда

= min (12 + 2, 11 + 5, 10 + 6) = 14, a₃ = 8.

Выпишем полученные условные оптимумы Z_k(a_k) и соответствующие им управления в виде таблицы:

Z0(1) = 0	Z3(8) = 12, a2 = 7
Z1(2) = 10, a0 = 1	Z3(9) = 11, a2 = 7
Z1(3) = 8, a0 = 1	Z3(10) = 10, a2 = 7
Z1(4) = 5, a0 = 1	Z4(11) = 14, a3 = 8
Z2(5) = 13, a1 = 2
Z2(6) = 11, a1 = 3, 4
Z2(7) = 8, a1 = 4

Очевидно, что

Остается определить сам путь S(1, 11), т.е. последовательность вершин, переводящую систему из a₀ = 1 в a₄ = 11. Такая последовательность в данном случае, как следует из модели, находится обратным ходом по условным экстремумам Z_k и условным управлениям u_k = a_k, полученным в результате решения функциональных уравнений. Эту процедуру называют безусловной оптимизацией. В результате получим

S(11, 1) = 11, 8, 7, 4, 1

или

S(1, 11) = 1, 4, 7, 8, 11.

Можно теперь определить длину найденного min пути S(1, 11) непосредственно: S(1, 11) = v₁(1, 4) + v₂(4, 7) + v₃(7, 8) + v₄(8, 11) = = 5+3+4+2 = 14. Задача решена.

Задача 2. Задача коммивояжера.

К этой задаче сводятся многие прикладные задачи, связанные с обслуживанием пространственно распределенных объектов (клиентов). Она представляет собой частный случай задачи маршрутизации, на которую наложены дополнительные условия (ограничения):

1. начальная и конечная вершины совпадают, a₀ = a_n;

2. все вершины должны быть пройдены, т.е. любая a_i  S(a₀, a_n);

3. каждая вершина проходится только один раз, т.е. (a_i, a_j   S(a₀, a_n))  (a_i  a_j);

4. известны расстояния между вершинами v(a_i, a_j), но не задана ориентация пар (a_i, a_j).

Конечно, принципиально модель ДП остается прежней. Но из-за этих условий вычислительная схема тактически становится несколько иной, приобретая ряд особенностей:

1. из-за условия 4 задача не имеет исходного графа. Очевиден лишь первый шаг, когда фиксирована вершина a₀;

2. по условию 2 очередной шаг может быть сделан только после выявления вершин, пройденных на предыдущих шагах;

3. при этом приходится отбрасывать варианты, в которых не выполняется условие 3;

4. из-за условия 1 задача не имеет обратного хода, так как с учетом сказанного обратный ход будет просто совпадать с прямым;

5. результаты решения функциональных уравнений целесообразно вынести на граф условных оптимумов, который, как инструмент перебора, позволяет не только выявить варианты решения при безусловной оптимизации, но и обнаружить варианты условной оптимизации на k-м шаге, т.е. организовать без ошибок k-й шаг.

Итак, модель задачи строится в процессе решения, так как очередной шаг можно определить только после условной оптимизации на предыдущем. Это связано с тем, что множество возможных состояний на данном шаге определяется не только множеством оптимальных состояний и управлений на предыдущем, но и условиями задачи. Иначе решение задачи выходит на полный перебор (n-факториал!).

Отсюда и особенность вычислительной схемы: граф задачи строится по шагам (т.е. функциональные уравнения очередного шага) по мере отыскания условных оптимумов и условных управлений на каждом предыдущем шаге в соответствии с условиями задачи. Таким образом, граф задачи, граф условных оптимумов и функциональные уравнения приходится строить и решать одновременно (см. иллюстрированный пример).

Иллюстративный пример

Пусть матрица стоимостей перехода из одного пункта в другой.

		1	2	3	4	5
	1	×	4	3	2	1
	2	4	×	4	3	2
	3	3	4	×	4	3
	4	2	3	4	×	4
	5	1	2	3	4	×

Условия: обход начинается и заканчивается в п. 3, все пункты должны быть пройдены, в один пункт нельзя заходить дважды. Z  max.

1. Граф задачи. Строится прямым ходом по шагам по мере решения функциональных уравнений, исходя из условий задачи (рис. 3.2).

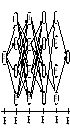
Рис. 3.2

Первый шаг очевиден. Последующие шаги делаются в зависимости от того, какие пункты пройдены.

2. Граф условных оптимумов. Наносятся все дуги (a_k–1, a_k), приводящие к max Z_k, 1 k  n (рис. 3.3).

Все max Z_k определяются из решения соответствующих функциональных уравнений. После выхода на E₅(a₅ = 3) обратным ходом находятся все варианты opt пути S(a₀, a₅), как это делалось в предыдущей задаче (безусловная оптимизация).

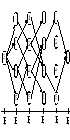
Рис. 3.3

3. Функциональные уравнения и их решение. Составляются для каждой вершины a_k  E_k графа задачи. Результат заносится на граф условных оптимумов, и определяется очередной (k+1)-й шаг для графа задачи в виде перечня дуг (a_k, a_k+1), исходя из условий задачи.

Z₀(a₀) = Z₀(3)  0.

Z₁(a₁) = Z₀(3) + v₁(3, a₁) = 0 + v₁(3, a₁).

Тогда

Z₁(1) = v₁(3, 1) = 3, a₀ = 3;

Z₁(2) = v₁(3, 2) = 4, a₀ = 3;

Z₁(4) = v₁(3, 4) = 4, a₀ = 3;

Z₁(5) = v₁(3, 5) = 3, a₀ = 3.

Наносим эти экстремумы на граф условных оптимумов в виде дуг (a₀, a₁) и определяем переход на E₂, т.е. дуги (a₁, a₂):

a1  a0	a2	дуги (a1, a2)
1  3	2, 4, 5	(1, 2), (1, 4), (1, 5)
2  3	1, 4, 5	(2, 1), (2, 4), (2, 5)
4  3	1, 2, 5	(4, 1), (4, 2), (4, 5)
5  3	1, 2, 4	(5, 1), (5, 2), (5, 4)

Полученные дуги наносим на граф задачи и производим шаг 2, т.е. строим уравнения Полученные экстремальные дуги (a₁, a₂) наносим на граф условных оптимумов и определяем переход на E₃. И т.д. до E₄. Таким образом, для E₂ имеем:

= max (4 + 4, 4 + 2, 3 + 1) = 8, a₁ = 2;

= max (3 + 4, 4 + 3, 3 + 2) = 7, a₁ = 1, 4;

= max (3 + 2, 4 + 3, 3 + 4) = 7, a₁ = 2, 5;

= max (3 + 1, 4 + 2, 4 + 4) = 8, a₁ = 4.

Наносим дуги (a₁, a₂) = (2, 1), (1, 2), (4, 2), (2, 4), (5, 4), (4, 5) на граф условных оптимумов и определяем переход на E₃:

a2  a1  a0	a3	дуги (a2, a3)
1  2  3	4, 5	(1, 4), (1, 5)
2  1  3	4, 5	(2, 1), (2, 4), (2, 5)
 4  3	1, 5
4  2  3	1, 5	(4, 1), (4, 2), (4, 5)
 5  3	1, 2
5  4  3	1, 2	(5, 1), (5, 2)

Наносим полученные дуги (a₂, a₃) на граф задачи и производим шаг 3, т.е. составляем и решаем уравнения

= max (7 + 4, 7 + 2, 8 + 1) = 11, a₂ = 2;

= max (7 + 3, 8 + 2) = 10, a₂ = 4, 5;

= max (8 + 2, 7 + 3) = 10, a₂ = 1, 2;

= max (8 + 1, 7 + 2, 7 + 4) = 11, a₂ = 4.

Снова наносим дуги (a₂, a₃) = (2, 1), (4, 2), (5, 2), (1, 4), (2, 4), (4, 5) на граф условных оптимумов и определяем переход на E₄, проверяя условие (3) для каждого варианта:

a3  a2  a1  a0	a4	дуги (a3, a4)
1  2  1  3	×	недопустимо
 4  3	5	(1, 5)
2  4  2  3	×	недопустимо
5  3	1	(2, 1)
5  4  3	1
4  1  2  3	5	(4, 5)
 2  1  3	5
 4  3	×	недопустимо
5  4  2  3	1	(5, 1)
 5  3	×	недопустимо

Наносим, как прежде, полученные дуги (a₃, a₄) на граф задачи и производим шаг 4, т.е. составляем и решаем уравнения

= max (10 + 4, 11 + 1) = 14, a₃ = 2;

= max (11 + 1, 10 + 4) = 14, a₃ = 3.

Переход (E₄  E₅) безусловный, так как возврат в п. 3 происходит при любом состоянии на E₄. Поэтому сразу получаем уравнение

= max (14 + 3, 14 + 3) = 17, a₄ = 1 и 5.

4. Граф вариантов решений. Является результатом безусловной оптимизации, проведенной на графе условных оптимумов обратным ходом, и строится очевидным образом начиная с a₅:

	a0 a1 a2 a3 a4 a5
×	3→ 2 → 4 → 2 → 1 → 3
(1)	3→ 5
(2)	3 → 4 → 5
(3)	3→ 2 → 1 → 4 → 5
(4)	3→ 1 → 2
×	3 → 4

Варианты, не удовлетворяющие условию 3, бракуются. Оставшиеся являются решением задачи:

S (a₀, a₅) = 3, 5, 4, 2, 1, 3 (1)

= 3, 4, 5, 2, 1, 3 (2)

= 3, 2, 1, 4, 5, 3 (3)

= 3, 1, 2, 4, 5, 3 (4)

Замечания к решению задачи

1. Изменение начала и направления обхода контура маршрута не приводит к изменению значения F_ц, так как при этом состав дуг маршрута не меняется. Следовательно, это приводит к эквивалентным решениям в разных вариантах задачи.

Таким образом, каждый вариант маршрута порождает 2n эквивалентных решений, из которых следует сохранить только одно. Если n = 5, то получим всего неэквивалентных решений, некоторые их них являютсяopt-ми.

2. Однако разные варианты задачи, отличающиеся началом обхода, могут и не содержать эквивалентных решений из-за невыполнения принципа оптимальности для тех из них, которые обладают свойством последействия. Поэтому полным решением задачи является совокупность всех неэквивалентных решений во всех вариантах задачи.

3. Перенумерация вершин графа с последующей их перестановкой в общем случае не приводит к эквивалентным решениям, так как состав дуг может измениться.

Задача 3. Оптимальное распределение ресурсов.

Модель демонстрирует связь ДП с ИМ. Обозначения оставим прежние:

n – число предприятий;

S – сумма средств (ресурсов), подлежащих распределению;

x_k – количество средств, выделяемых k-му предприятию;

_k(x_k) – показатель эффективности k-го шага (задается).

1. Тогда суммарный показатель эффективности

при условии: (тип 2)

2. Определим S_k – параметр состояния системы на k-м шаге.

Определение I. Пусть S_k – сумма средств, выделенных первым k предприятиям:

Тогда

S_k = S_k–1 + x_k (для обр. хода) (тип 1₁)

или

S_k = S_k+1 – x_k+1 (для пр. хода)

(так как S_k–1 = S_k – x_k).

Определение II. Пусть S_k – сумма средств, оставшихся после выделения первым k предприятиям:

Тогда

S_k = S_k–1 – x_k (для обр. хода) (тип 1₂)

или

S_k = S_k+1 + x_k+1 (для пр. хода)

(так как S_k–1 = S_k + x_k).

3. Задачу теперь можно сформулировать следующим образом: требуется определить n переменных x₁, x₂,…, x_n, удовлетворяющих уравнению состояния и оптимизирующих Z, т.е. Z  opt.

4. Введем в рассмотрение суммарный показатель эффективности k-го шага, т.е. переменную Z_k:

Z_k = Z_k(S_k–1, x_k) для прямого хода и

Z_k = Z_k(S_k–1, x_k+1) для обратного хода.

Используя уравнение состояний (1) для соответствующего хода, можно записать:

Z_k(S_k–1, x_k) = Z_k(S_k) для прямого хода и

Z_k(S_k–1, x_k+1) = Z_k(S_k) для обратного хода.

Получили однотипную запись для Z_k независимо от хода и определения переменной состояния S_k (т.е. так же, как в ИМ).

5. Тогда функциональные уравнения Беллмана будут выглядеть следующим образом:

– для прямого хода:

Z₁(S₁) = ₁(x₁), так как Z₀  0; (тип 3')

(тип 4')

– для обратного хода:

Z_n–1(S_n–1) = _n(x_n), так как Z_n  0; (тип 3)

(тип 4)

Замечание. Уравнения Беллмана не зависят от определения переменной состояния S_k.

6. В результате решения уравнений (3, 4) или (3', 4') получаем две последовательности функций: условные оптимумы суммарного показателя эффективности {Z_k(S_k)} и условные управления {x_k(S_k)} на k-м шаге. При этом opt Z = Z_n для прямого хода и opt Z = Z₀ для обратного.

Тем самым становятся известными и последовательности  S_k, k = 1,…, n  при прямом ходе или  S_k, k = n – 1,…, 0  при обратном, так как Z_k = Z_k(S_k), где S_k фиксировано.

7. Безусловная оптимизация: используя обе последовательности  S_k  и  x_k(S_k) , записанные в обратном порядке, и соответствующее уравнение состояний и руководствуясь общей вычислительной схемой ДП, т.е. строя последовательность состояний и управлений противоположным ходом, получим значения переменных x_k на каждом шаге.

Задача 4. Оптимальное управление запасами.

1. Содержательная постановка задачи.

Планируемый период разделен на n промежутков времени (дни, месяцы и т.д.), в которых задан расход d_k, производимый в конце каждого промежутка. Известны также начальный уровень запасов и зависимость суммарных затрат на хранение и пополнение запасов в данном периоде от среднего уровня хранимых запасов и их пополнения. Требуется определить размеры пополнения запасов в каждом промежутке времени для удовлетворения заданного расхода из условия минимума суммарных затрат за весь период.

2. Введем обозначения. Пусть n – число промежутков времени,

u_k – размер пополнения запасов в k-м промежутке (переменная управления),

S_k–1 – уровень запаса в начале k-го промежутка, т.е. после расхода в (k – 1)-м (переменная состояния),

S₀ – начальный уровень запасов (задано),

d_k – расход в k-м промежутке (задано).

И пусть затраты вk-м промежутке, где средний уровень запаса.

Если

Тогда суммарные затраты выразятся формулой:

(тип 2')

А уравнение состояния (балансовое уравнение) запишется в виде:

S_k = S_k–1 + u_k – d_k (тип 1')

(или S_k–1 = S_k – u_k + d_k) – для прямого хода.

Напомним, что S_k – уровень запаса в конце k-го промежутка.

Ограничения: S_k  0, u_k  0.

Задача теперь приобретает стандартную формулировку: требуется определить n переменных  u₁, u₂,…, u_n , удовлетворяющих (1') и минимизирующих (2').

3. Функциональные уравнения:

(тип 3')

или

= f₁ (S₀, u₁),

если S₀ – единственно;

(тип 4')

Остается определить допустимые пределы изменения u_k. Из ограничений и уравнения состояний (1') следует:

S_k–1 = S_k – u_k + d_k  0,

откуда

u_k  S_k + d_k.

Таким образом, 0  u_k  S_k + d_k.

Замечание. Задача не имеет обратного хода, так как конечное состояние S_n заранее не известно.

4. В результате решения функциональных уравнений получим последовательно все условные оптимумы Z_k и условные управления u_k для каждого шага:

{Z₁(S₁), u₁(S₁)},…, {Z_n(S_n), u_n(S_n)}.

При этом min Z = Z_n(S_n). Так как S_n фиксировано, u_n = u_n(S_n) становится известным. Теперь можно последовательно обратным ходом провести безусловную оптимизацию и определить значения всех u_k:

……………………………

В результате получим вектор оптимальных значений  u₁, u₂,…, u_n , который минимизирует Z, а значит, является решением задачи.

Задача 5. Задача «о замене оборудования».

1. Задано: начальная стоимость оборудования, стоимость произведенной продукции на этом оборудовании, ежегодные затраты на эксплуатацию оборудования, ликвидная стоимость.

Определить оптимальные сроки замены оборудования в течение n лет, при которых прибыль от эксплуатации оборудования была бы максимальной.

2. Введем обозначения. Пусть n – период эксплуатации,

t₀ – возраст оборудования в начале планового периода (задано),

t – возраст оборудования в течение планового периода,

p – начальная стоимость оборудования,

f(t) – стоимость произведенной продукции на оборудовании возраста t лет,

r(t) – ежегодные затраты на эксплуатацию оборудования возраста t лет,

(t) – ликвидная стоимость оборудования возраста t лет.

Замечание. Отсутствует единый показатель эффективности k-го шага. Поэтому суммарный показатель эффективности Z нельзя выразить формулой, единой для всех шагов.

3. Пусть k-й шаг есть номер k-го года. Тогда для k-го шага t = = 0, 1, 2,…, k – 1; т.е. t  k – 1. А состояние системы в начале k-го шага S_k–1 = t, t = 0, 1, 2,…, k – 1.

Если управление на k-м шаге

то уравнение состояния тогда запишется в виде:

(тип 1)

4. Пусть Z(t₀ + t) – прибыль от эксплуатации оборудования в течение t лет. При отсутствии определения Z задачу можно сформулировать неформально следующим образом: требуется определить оптимальные сроки замены оборудования в течение n лет при условии Z = max (т.е. определить точку замены на шкале t).

5. Поскольку здесь нет показателя эффективности k-го шага f_k, нельзя выразить Z как суммарную величину через f_k. Однако суммарный показатель эффективности для k-го шага Z_k можно выразить через f(t), r(t) и (t) в зависимости от управления на каждом шаге.

Положим t₀ = 0, тогда функциональное уравнение для n-го шага (при обратном ходе) запишется в виде:

(тип 3)

Сравнив эти две величины для всех t > n, получим условный оптимум Z_n (t) и условное управление u_n (t).

Предположим, что для всех значений S_k = t известна максимальная прибыль Z_k+1 (S_k), полученная за (n – k) шагов с (k + 1)-го по n-й включительно. Тогда функциональное уравнение для k-го шага запишется в виде:

(тип 4)

где Z_k+1 – условная оптимальная прибыль за (n – k) шагов, если к началу (k + 1)-го шага S_k = 1 или S_k = S_k–1 + 1 = t + 1 по (1).

В результате решения этих уравнений получаем, как всегда, две последовательности функций: условных оптимумов Z_k (t) и условных управлений u_k(t) для каждого k-го шага. При этом для S₀ = t₀ имеем:

max Z = Z₁(t₀ + t) = Z₁(t₀),

так как t = 0 по определению.

6. Безусловная оптимизация заключается в выборе из множества {u_k(t)} только безусловных управлений. По обратной цепочке (т.е. прямым ходом) с помощью уравнения (1) получим:

u₁ = u₁(t₀), из (1)  (S₁ = t₁);

u₂ = u₂(t₀), из (1)  (S₂ = t₂);

……………………………..

u_n = u_n(t_n–1),

где t_k – фиксированное значение t в зависимости от u_k; t_k =  t₀ + k, k, k – 1,…, 1 .

Решением задачи является оптимальное управление U = (u₁, u₂,…, u_n), представляющее собой набор двузначных переменных u_k = = u^c, u^з.

Замечание. В принципе число вариантов управления, т.е. число значений u_k, может быть более двух, что не меняет существа модели.