
- •Б.К. Алабин
- •1.2. Основные понятия и определения исследования операций
- •1.3. Общая постановка задачи исследования операций
- •Тема 2 индексный метод (теория графов)
- •2.1. Основные понятия и определения индексного метода (им)
- •2.2. Постановка задачи маршрутизации в им
- •2.3. Идея решения задачи
- •2.4. Алгоритм решения задачи с помощью произвольного дерева маршрутов
- •2.5. О порядковой функции
- •2.6. Общая теория индексного метода на матрице орграфа
- •2.7. Общий алгоритм решения задачи маршрутизации на матрице орграфа
- •2.8. Иллюстративный пример
- •2.9. Последовательные графы в им
- •2.10. Решение задачи распределения ресурсов индексным методом
- •3.4. Условия, которым должна удовлетворять задача, описываемая моделью дп
- •3.5. Вычислительная схема дп для обратного хода
- •3.6. Особенности вычислительной схемы дп для прямого хода
- •3.7. Основные достоинства метода дп
- •3.8. Типовые задачи в моделях дп
- •Тема 4 методы линейного программирования (лп)
- •4.1. Систематизация моделей лп
- •4.2. Возможные исходы решения задач лп
- •4.3. Транспортная задача (т-задача)
- •Метод потенциалов для оценки Δij в т-задаче
- •Замечания к решению т-задачи
- •4.4. Задача «о назначениях»
- •4.5. Задача планирования производства при фиксированном фонде времени
- •Иллюстративный пример
- •Тема 5 задача и модель «черного ящика»
- •5.1. Общие замечания
- •5.2. Содержательная постановка задачи
- •5.3. Формальная постановка задачи
- •5.4. Математическая модель и математическая постановка задачи
- •5.5. О решении задачи
- •5.6. Иллюстративный пример
- •Рекомендуемая литература
- •Содержание
2.5. О порядковой функции
При таком способе действий некоторые дуги приходится просматривать более одного раза. Этого можно избежать, если просматривать дуги в определенном порядке, т.е. упорядочить их. Такой порядок можно задать, введя порядковую функцию на множестве А.
Определение. Порядковой функцией на орграфе без контуров называется функция, которая разбивает множество вершин графа на упорядоченные подмножества Еi по правилу: вершина аi Еi, если она достижима из а0 не более чем за i шагов.
Множество Еi обычно называют уровнями.
Для предыдущего примера порядковую функцию можно задать следующим образом (рис. 2.2).
6


Е

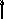 0
= {1}
0
= {1}
Е1 = {2, 4}
Е 1
7
2












Е

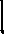
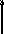 3
= {5}
3
= {5}
Е
 4
= {7}
4
= {7}
3


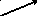

4
5





Рис. 2.2
Упорядочив вершины по уровням, получим (рис. 2.3).
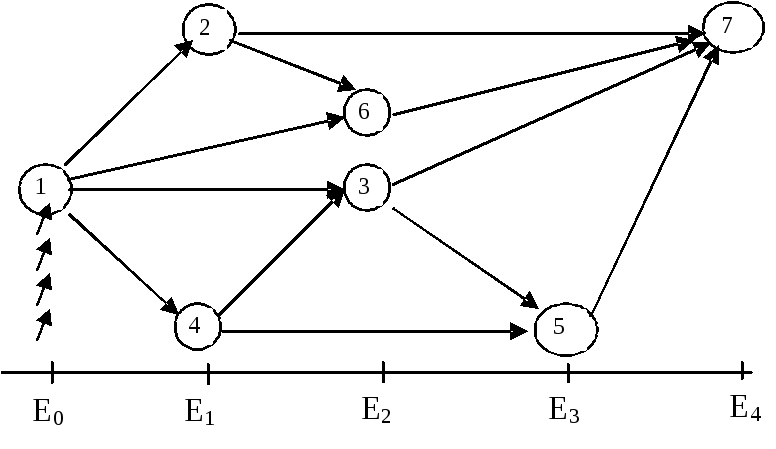
Рис. 2.3
Свойства упорядоченного графа:
1) все дуги расположены в направлении от начальной вершины к конечной; следовательно, при просмотре дуг антидерева в указанном порядке (см. шаг 4 б) ни одна вершина не проходится дважды, поэтому при смене дуг индексы предыдущих вершин не меняются, а перебор равен числу дуг антидерева;
2) вершины одного уровня не связаны дугами; следовательно, порядок просмотра вершин одного уровня безразличен.
2.6. Общая теория индексного метода на матрице орграфа
Соберем все полученные результаты воедино и обобщим их на матрице орграфа.
Лемма 1. В любом орграфе без контуров всякое множество дуг, взятых по одной из каждого столбца (строки) его матрицы, образует дерево с корнем в начальной (конечной) вершине.
Принцип оптимальности. Всякий подпуть оптимального пути на графе без контуров есть оптимальный путь. Не работает, когда проявляется последействие.
Определение 1. Opt деревом орграфа без контуров называется дерево, индексы всех вершин которого оптимальны. Поэтому всякий путь в opt дереве является оптимальным. Отсюда следует, что для opt дерева справедлив принцип оптимальности.
Следствие 1. Лемма 1 позволяет по матрице орграфа перечислить все его деревья, содержащие путь от начальной вершины до конечной (или от конечной до начальной), и выбрать среди них оптимальное, т.е. содержащее искомый оптимальный путь (полный перебор!).
Определение 2. Порядковой функцией на орграфе без контуров называется такая функция, которая разбивает множество вершин графа на упорядоченные подмножества Еi по правилу: аi Еi, если аi достижима из а0 не более чем за i шагов (или из аn не более чем за (n – i) шагов). Порядковая функция строится для задания порядка при просмотре дуг антидерева.
Признак порядка на матрице орграфа: граф обладает порядковой функцией, если все значимые элементы его матрицы находятся над главной диагональю.
Лемма 2. Opt дерево для орграфа без контуров может быть построено непосредственно направленным перебором его входящих (исходящих) дуг последовательно по столбцам (или строкам) в соответствии с его порядковой функцией, начиная с корневой вершины, начальной или конечной, т.е. прямым или обратным ходом.
Следствие 2. Лемма 2 дает способ построения с минимальным перебором opt дерева, содержащего оптимальный путь от корневой вершины до любой другой в соответствии с принципом оптимальности.
