2.9. Последовательные графы в им

В предыдущем примере для решения задачи маршрутизации была использована математическая модель в виде орграфа без контуров, на котором строилась порядковая функция. Оказывается, эту модель можно упростить, сведя ее к последовательному графу, тем более что многие прикладные задачи могут быть сформулированы на последовательном графе как на модели.

Пусть на орграфе без контуров задана порядковая функция, т.е. все вершины графа распределены по уровням Е₀, Е₁,…, Е_n.

Определение. Последовательным графом называется такой орграф без контуров, в котором множество дуг, исходящих из вершин уровня Е_i, совпадает с множеством дуг, входящих в вершины уровня Е_{i + 1}.

По определению последовательный граф всегда обладает порядковой функцией. Достоинства последовательного графа:

1. можно оптимизировать по частям;

2. порядок индексации вершин можно изменить на обратный (от прямого хода перейти к обратному), для этого достаточно заменить порядковую функцию на обратную;

3. любой орграф без контуров можно превратить в последовательный, введя дополнительные вершины и дуги с нулевым весом.

Пример (продолжение предыдущего) (рис. 2.5).

Рис. 2.5

Применение последовательного графа в качестве математической модели позволяет существенно упростить технически реализацию индексного метода.

2.10. Решение задачи распределения ресурсов индексным методом

Введем обозначения:

S – начальная сумма ресурса (средств), выраженная в некотором масштабе;

n – число предприятий;

x_i – средства, выделяемые i-му предприятию;

φ_i(x_i) – функции дохода (издержек) для i-го предприятия (задано!).

Условие:

Пример (исходные данные).

Пусть S = 3 (в масштабе), n = 4.

xi	φ1(x1)	φ2(x2)	φ3(x3)	φ4(x4)
0 1 2 3	5 8 10 11	3 6 9 11	2 3 4 7	2 5 6 8

Задача. При заданном условии найти такое распределение заданной суммы средств S по n предприятиям (x_i = ?), при котором

Решение этой задачи сводится к решению задачи маршрутизации на последовательном графе. Обратимся к его построению.

Пусть один шаг есть выделение средств очередному предприятию. При n = 4 имеем 4 шага. Тем самым определены уровни Е_i для последовательного графа: Е₀, Е₁,…, Е₄.

Для каждого шага введем параметр состояния S_i и для каждого значения переменной S_i отведем вершину а_i  E_i последовательного графа. Таким образом, каждая вершина графа а_i получает имя виде значения переменной S_i на уровне E_i. Определим переменную S_i.

I определение переменной состояния. Пусть S_i есть сумма средств, выделенных первым i предприятиям:

S_i = 0, 1,…, S; i = 0, 1, 2,…, n.

Соответственно S₀ = 0, S_n = S. Тем самым определены начальная и конечная вершины графа: a₀ = S₀, a_n = S_n. Для нашего примера a₀ = 0, a₄ = 3.

Определим состав уровня Е₁. Ясно, что первому предприятию можно выдать любую сумму средств от нуля до S, т.е. в примере х₁ = 0, 1, 2, 3. А значит, переменная состояния S₁ принимает те же значения, так как S₁ = х₁. Следовательно, a₁ = S₁ = 0, 1, 2, 3, т.е. Е₁ = {0, 1, 2, 3}. При этом определяются и веса дуг: v(a₀, a₁) = x₁(a₀, a₁). В нашем примере имеем:

v(0, 0) = 0,

v(0, 1) = 1,

v(0, 2) = 2,

v(0, 3) = 3.

Обратимся к построению уровня Е₂. Ясно, что второму предприятию можно выделить средств не более остатка после выделения первому. А так как S₂ = x₁ + x₂ = S₁ + x₂ и, как и S₁, не превышает S, то для данного примера имеем:

– если S₁ = 0, то x₂ = 0, 1, 2, 3; S₂ = 0, 1, 2, 3;

– если S₁ = 1, то x₂ = 0, 1, 2; S₂ = 1, 2, 3;

– если S₁ = 2, то x₂ = 0, 1; S₂ = 2, 3;

– если S₁ = 3, то x₂ = 0; S₂ = 3.

При этом S₂, как и S₁, пробегает те же значения, т.е. S₂ = 0, 1, 2, 3. А значит, и а₂ = 0, 1, 2, 3 на уровне Е₂, причем:

– для а₂ = 0 имеем одну входящую дугу;

– для а₂ = 1 имеем две входящих дуги;

– для а₂ = 2 имеем три входящих дуги;

– для а₂ = 3 имеем четыре входящих дуги.

Все последующие уровни Е_i, 2 < i < n, строятся совершенно аналогично, так как S_i = S_i – 1 + x_i ≤ S. Исключение составляет последний шаг, т.е. переход к E_n, где по условию S_n = S в точности.

Построенный граф, в котором a_i = S_i, очевидно, является последовательным и выглядит следующим образом (рис. 2.6).

На таком графе еще нет задачи, так как для любого пути S(a₀, a_n) его длина равна

по условию.

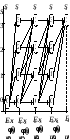
Рис. 2.6

Задача возникает, когда дугам в соответствии с х_i приписывается функция дохода (или издержек) φ_i(x_i) в качестве веса. Возникающую при этом суммарную величину

на каждом i-м шаге и следует оптимизировать. Как и S_i, функция F(S_i) приписывается вершинам в качестве веса. В таком случае F(S_i) = = I(a_i), так как a_i = S_i на графе.

Следовательно, исходная задача распределения ресурсов свелась к разобранной выше задаче маршрутизации на последовательном графе, поэтому

F(S_i) = F(S_{i – 1}) + φ_i(x_i),

F(S₀) ≡ 0,

оpt F_ц = F(S_n)

при прямом ходе.

При обратном ходе, как и в задаче маршрутизации, будем иметь:

F(S_i) = F(S_{i + 1}) + φ_{i + 1}(x_{i + 1}),

F(S_n) ≡ 0,

оpt F_ц = F(S₀).

Замечание. Чтобы помнить, какие величины фигурируют на графе, полезно иметь в виду табличку:

	Дуги	Вершины
1)	xi
2)	φi(xi)

II определение переменной состояния.

Пусть S_i – есть остаток средств после выделения первым i предприятиям:

S_i = S, S – 1,…, 0.

Для построения графа задачи здесь применяется та же схема рассуждений, но с единственной поправкой: S_i(II) = S – S_i(I). Эта по-

правка приводит к тому, что

S₀ = S – 0 ≡ S,

S₁ = S – x₁,

S₂ = S – (x₁ + x₂),

………………

S_n = S – S ≡ 0.

Все остальные переменные сохраняют прежний смысл.

Читателю полезно провести это построение самостоятельно, сделав замену S_i(II) = S – S_i (I). В результате также получим последовательный граф, но симметричный первому (рис. 2.7).

И последнее. Решая исходную задачу как задачу маршрутизации на последовательном графе, независимо от определения переменной состояния S_i получим opt последовательность вершин a₀ a₁… a_n (или a_n a_n–1… a_o), соответствующую последовательности состояний S₀ S₁… S_n (или S_n S_n–1… S₀). Однако это еще не решение задачи распределения ресурсов, так как требуется от переменных состояния S_i перейти к переменным управления х_i. Сделать это можно, используя определение S_i. Действительно, независимо от хода для I определения переменной S_i будем иметь: x_i = S_i – S_i – 1, так как S_i монотонно не убывающая величина. При II определении S_i – монотонно не возрастающая величина. Поэтому x_i = S_i – 1 – S_i.

Рис. 2.7

Таким образом, в любом случае x_i = |S_i – S_i – 1| независимо ни от хода, ни от определения переменной состояния S_i. В результате получим последовательность переменных х₁ х₂… х_n, при которой целевая функция F_ц = opt. Задача решена.

Тема 3

МЕТОД ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ (ДП)

3.1. Общее замечание

Принципиально постановки всех задач, решаемых методом ДП, отличаются:

1. показателем эффективности, который определяет критерий эффективности (целевая функция);

2. видом уравнения состояний.

Оба определяют основные для вычислительной схемы функциональные уравнения (уравнения Беллмана). По форме функциональные уравнения не отличаются, поэтому и вычислительная схема для всех задач неизменна.

3.2. Общая постановка задачи ДП

Пусть S_o – начальное состояние системы, S_n – конечное состояние системы, U (иногда X) – допустимое управление системой (набор допустимых показателей), Z = Ф(S_o, U) или Z = Ф(S_n, U) – показатель эффективности (целевая функция).

Требуется определить допустимое управление системой U, переводящее систему из начального состояния S₀ в конечное S_n, при котором Z достигает оптимума (максимума или минимума).

3.3. Построение модели ДП (для обратного хода)

1. Выбирают способ деления процесса на шаги.

2. Вводят в рассмотрение переменные состояния S_k и переменные управления u_k на каждом шаге процесса, 1  k  n.

3. Записывают уравнение состояния

S_k = F (S_k–1, u_k). (тип 1)

4. Вводят в рассмотрение заданный показатель эффективности на k-м шаге f_k (S_k–1, u_k) и записывают суммарный показатель (целевую функцию)

(тип 2)

5. Вводят в рассмотрение условные оптимумы показателя эффективности Z_k(S_k–1) от k-го шага (включительно) до конца процесса и условные оптимальные управления на k-ом шаге u_k (S_k–1).

6. Из ограничений задачи определяют для каждого шага множества D_k допустимых управлений на этом шаге.

7. Записывают основные для вычислительной схемы ДП функциональные уравнения Беллмана:

(тип 3)

так как еслиилиесли

(тип 4)

Таким образом, в результате для конкретной задачи получаем модель ДП в виде системы (n + 2) уравнений, в которой различаются 4 типа уравнений:

1. уравнение состояний S_k =…,

2. общий суммарный показатель эффективности: Z =…,

3. условный оптимум показателя эффективности для исходного шага Z_n (или Z₀) =…,

4. условный оптимум суммарного показателя эффективности для каждого k-го шага Z_k =…