- •1.Определенный интеграл Римана. Основные определения. Необходимое условие интегрируемости. Суммы Дарбу и их свойства. Условие интегрируемости.
- •2. Критерий интегрируемости функций. Классы интегрируемых функций. Свойства интеграла, связанные с операциями над функциями.
- •3. Свойства интеграла, связанные с отрезками интегрирования и неравенствами. Оценки интегралов.
- •4. Теоремы о среднем.
- •5. Непрерывность и дифференцируемость интеграла по верхнему пределу.
- •6. Теорема (формула) Ньютона-Лейбница.
- •7. Теорема о замене переменной в определенном интеграле, формула интегрирования по частям в определенном интеграле.
- •8. Площадь фигуры на плоскости (клеточные фигуры, квадрируемые фигуры, мера). Площадь криволинейной трапеции, криволинейного сектора, площадь фигуры с параметрически заданной границей.
- •9. Объем тела (клеточное тело, кубируемое тело, мера). Объем цилиндрического тела, объем тела с заданными площадями сечений, объем тела вращения.
- •10. Длина кривой (определение спрямляемой кривой, длины кривой, теорема о длине, формулы длины для разных случаев задания кривой).
- •11. Площадь поверхности вращения (определение, теорема). Теорема Гульдена. Физические приложения определенных интегралов.
- •12. Несобственные интегралы первого рода (определение; свойства, включая интегрирование по частям и формулу Ньютона-Лейбница.
- •13. Несобственные интегралы второго рода (определение; свойства, включая интегрирование по частям и формулу Ньютона-Лейбница.
- •14. Условие сходимости несобственных интегралов. Несобственные интегралы от неотрицательных функций – признаки сходимости.
- •15. Признаки Дирихле и Абеля сходимости несобственных интегралов.
- •16. Абсолютная и условная сходимость несобственных интегралов (определение, теорема).
- •17. Метрическое пространство (определение, сходящиеся и фундаментальные последовательности, полное пространство, открытые и замкнутые множества, компакт, пространство ).
- •18. Функции многих переменных. Предел функции в точке, предел по множеству, по направлению.
- •19. Непрерывность функции многих переменных в точке. Свойства непрерывных функций. Непрерывность функции на множестве, свойства функций, непрерывных на компакте.
- •20. Частные производные, дифференцируемость, дифференциал. Теоремы о необходимых и достаточных условиях дифференцируемости функции многих переменных.
- •21. Дифференцируемость сложной функции. Инвариантность формы 1-го дифференциала. Правила дифференцирования.
- •22. Геометрический смысл 1-го дифференциала. Касательные плоскость и нормаль. Производная по направлению. Градиент.
- •23. Частные производные высших порядков. Теорема о равенстве смешанных производных.
- •24. Дифференциалы высших порядков (определение, формы записи, неинвариантность 2-го и высших дифференциалов.
- •25. Формула Тейлора для функции многих переменных.
- •26. Теорема о неявной функции.
- •27. Дифференцируемое отображение. Якобиан и его свойства. Системы функций, заданных неявно – теорема. Якобиан и зависимость – независимость функций.
- •28. Локальный экстремум функции многих переменных. Необходимые условия экстремума.
- •29. Достаточные условия экстремума функции многих переменных. Проверка экстремума для функции двух переменных.
- •30. Условный экстремум: прямой метод, метод Лагранжа.
- •31. Числовые ряды (понятие ряда, сходимость, частичная сумма, сумма). Необходимый признак сходимости ряда. Свойства сходящихся рядов. Критерий Коши.
- •32. Ряды с неотрицательными членами. Признаки сходимости: через частичные суммы, интегральный признак.
- •33. Ряды с неотрицательными членами. Признаки сравнения и его следствия.
- •34. Признаки Даламбера и Коши сходимости ряда.
- •35. Знакочередующийся ряд. Признак сходимости Лейбница, следствие.
- •36. Абсолютная и условная сходимость ряда (определение, свойства абсолютно-сходящихся рядов). Примеры исследования сходимости ряда. Признаки Абеля и Дирихле.
- •37. Функциональные последовательности и ряды: сходимость, равномерная сходимость, связь утверждений о функциональных последовательностях и рядах.
- •38. Критерий Коши равномерной сходимости, признак Вейерштрасса.
- •39. Признак Абеля и Дирихле равномерной сходимости ряда. Свойства равномерно сходящихся последовательностей и рядов – непрерывность предельной функции и суммы ряда.
- •41. Степенные ряды. Теорема Абеля, радиус сходимости, круг (интервал) сходимости, формула Коши-Адамара.
- •42. Формула Даламбера для радиуса сходимости степенного ряда. Теорема о почленном дифференцировании и интегрировании степенного ряда. Аналитическая функция, единственность коэффициентов.
- •43. Ряд Тейлора. Достаточные условия разложимости функции в ряд Тейлора. Ряды Маклорена для элементарных функций.
- •44. Ортогональная система функций. Ряды Фурье. Тригонометрический ряд Фурье, формулы для коэффициентов. (Ряды Фурье для четных и нечетных функций).
- •45. Лемма Римана, ядро Дирихле, формула Дирихле для частичных сумм. Признак Дини сходимости ряда Фурье.
- •46. Признак Дирихле сходимости ряда Фурье. Простейшие условия равномерной сходимости ряда Фурье. Почленное дифференцирование и интегрирование ряда Фурье.
29. Достаточные условия экстремума функции многих переменных. Проверка экстремума для функции двух переменных.
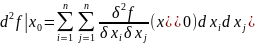 тогда ⇒
тогда ⇒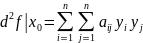 , y=
-квадратичная
форма.
, y=
-квадратичная
форма.
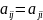 ,
А=(
,
А=(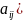 -
симметричная
матрица.
-
симметричная
матрица.
А(y)=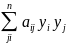 квадратичная
форма для (y
квадратичная
форма для (y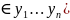 .
.
Определение:
1)
Квадратичная
форма называется положительно-определенной,
если А(y)>0
y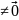 .
.
2) Квадратичная форма называется отрицательно-определенной, если А(y)<0 y .
3)
Квадратичная форма называется
знакопеременной, если
 ,
.
А(
)>0,
А(y)<0.
,
.
А(
)>0,
А(y)<0.
4) Квадратичная форма называется неотрицательно-определенной, если А(y)≥0 y.
5) Квадратичная форма называется неположительно-определенной, если А(y)≤0 y.
Теорема Сильвестра (Критерий Сильвестра):Пусть А=( матрица квадратичной формы А(y), .
1)
Квадратичная
форма положит. определяется тогда и
только тогда
 когда
все угловые
миноры положительны:
когда
все угловые
миноры положительны: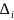 >0,
i=1,
.
>0,
i=1,
.
2)
Квадратичная
форма отрицат. определяется
когда
знаки угловых
миноров чередуются,
 <0,
т.е.
=
<0,
т.е.
=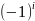 , i=1,
.
, i=1,
.
Угловым минором k-го порядка матрицы А называют минор, стоящий в верхнем левом углу матрицы А.
 ,
,
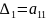 ,
,
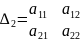 .
.
Теорема
1(необходимое условие экстремума): Если
функция f(x)
имеет в точке
экстремум и в некоторой окрестности
точки
имеет производные второго порядка,
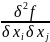 непрерывные в
точке
.
Тогда
непрерывные в
точке
.
Тогда
 и
и
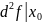 ≥0
неотрицательно-определенная квадратичная
форма, если в
точке
локальный минимум или
≤0
если в точке
экстремум максимум.
≥0
неотрицательно-определенная квадратичная
форма, если в
точке
локальный минимум или
≤0
если в точке
экстремум максимум.
Теорема
2(достаточное условие экстремума): Пусть
выполнены следующие условия: 1)
- стационарная точка функции
(т.е.
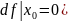 .
2)
в некоторой окрестности точки
и непрер. в точке
.
Тогда, если
положительно-определенная квадратичная
форма, то функция f(x)
имеет в точке
локальный экстремум минимум. Если
отрицательно-неопределенная квадратичная
форма, то функция f(x)
имеет в точке
локальный экстремум максимум. Если
знакопеременная квадратичная форма,
то функция f(x)
не имеет
экстремума в точке
.
.
2)
в некоторой окрестности точки
и непрер. в точке
.
Тогда, если
положительно-определенная квадратичная
форма, то функция f(x)
имеет в точке
локальный экстремум минимум. Если
отрицательно-неопределенная квадратичная
форма, то функция f(x)
имеет в точке
локальный экстремум максимум. Если
знакопеременная квадратичная форма,
то функция f(x)
не имеет
экстремума в точке
.
Доказательство: воспользуемся формулой Тейлора 2-го порядка в форме Пеано в точке f(x)=f( )+
+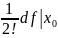 +0
(
+0
(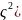 ,
где
=
;
f
=
,
где
=
;
f
=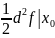 +0
(
=
+0
(
=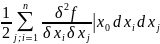 +
+
0
(
= (
(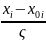 )
(
)
(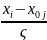 )+
(
=
)+
(
=
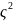 (
(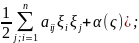 =
=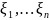 (
(
A
(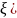 -
квадратичная форма задана на сфере в
-
квадратичная форма задана на сфере в
A ( принимает в какой-то точке наименьшее значение.
1 квадратичная форма (2 дифф.) положительно-определенная A ( >0 ; m=i n f A ( >0.
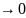 для
для
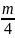 бетта: {
бетта: {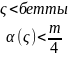
f
=
(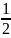 A
(
A
( )>
)>
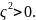
3 случай: Если знакопеременная квадратичная функция, то по теореме 1 в точке не может быть не локального максимума, не локального минимума ⇒ экстремума нет.
Исследование на экстремум функции 2-ух переменных
Пусть функция U= f(x, y) дифф. в точке , , и имеет 2-ые непр. частные производные в этой точке. Пусть точка - стационарная точка функции f.
{
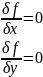 ⇒
⇒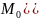 ,
,

A=(
 и
A
и
A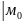 =(
=(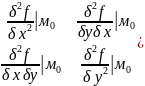 .
.Если (A
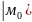 >0
экстремум
есть.
>0
экстремум
есть.
а)
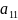 =
>0,
то экстремум минимум
=
>0,
то экстремум минимум
б) если
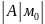 <0
экстремума нет.
<0
экстремума нет.
г) если =0 требуется дополнительное исследование, а именно есть или нет экстремум,
f , меняет или не меняет знак в окрестностях точки ,
30. Условный экстремум: прямой метод, метод Лагранжа.
Пусть
в Д
⊂
определенной функции
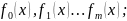 m<n.
Пусть
S
–множество
точек области Д
удовлетворяющих
системе уравнений:
m<n.
Пусть
S
–множество
точек области Д
удовлетворяющих
системе уравнений:
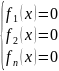 (*)
(*)
т.е. S –поверхность, заданная (*) в .
Уравнения (*) будем называть уравнениями связей (или просто связями).
Рассмотрим
функцию
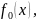 когда x
S,
имеет
ли функция
когда x
S,
имеет
ли функция
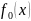 экстремум в точке
S
при
условии, что рассматриваемые точки
экстремум в точке
S
при
условии, что рассматриваемые точки
 S,
т.е.
координаты удовлетворяют уравнению
(*).
S,
т.е.
координаты удовлетворяют уравнению
(*).
Определение:
Говорят,
что
имеет в точке
S
экстремум
максимум (минимум) при наличии уравнений
связи (*) или говорят имеет условный
экстремум максимум (минимум) если
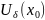 ,
что
x
,
что
x
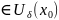 S⇒
f(x)≤
f(
)(
для
минимума: f(x)≥
f(
)).
S⇒
f(x)≤
f(
)(
для
минимума: f(x)≥
f(
)).
Два метода решения задач на условный экстремум.
1)Прямой метод нахождения условного экстремума (метод исключения неизвестных). Предположим, что (*) позволяет однозначно выразить какие-либо m переменных через остальные (m-n) переменных.
Пусть
переменные
…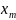 выражаются из (*) через остальные
переменные.
выражаются из (*) через остальные
переменные.
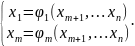 Выражаем
(**) подставляем в
Выражаем
(**) подставляем в
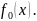
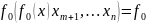 (
( ,
,
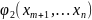 ,
…
,
…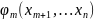 ,
,
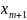 ,
…
,
…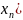 =
=
F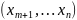 - исследование на экстремум как функцию
n-m
переменных.
- исследование на экстремум как функцию
n-m
переменных.
2)Метод множителей Лагранжа.
Определение:
при
исследовании на экстремум функции
при наличии уравнений связи (*) строится
функция Лагранжа. Обозначается: L
(x,
λ), где
x=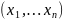 ,
λ=
,
λ=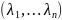 и
равная L
(x,
λ)=
и
равная L
(x,
λ)=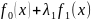 +
+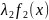 +…
+
+…
+
Стационарной
точкой функции Лагранжа называется
точка
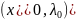 ,
координаты которой система уравнений:
,
координаты которой система уравнений:
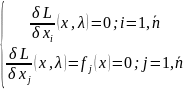
Теорема
1: 1)
Пусть в точке
- условный экстремум в
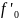 (x)
при наличии функций связи (*):
(x)
при наличии функций связи (*):
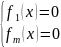 .
.
2)Пусть
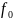 (x),
(x),
 …
… непр.
дифф. в некоторой окрестности точки
непр.
дифф. в некоторой окрестности точки
3)В
точке
матрица Якоби системы функций
…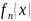
Ф'(x)=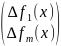 имеет
ранг=m.
имеет
ранг=m.
(Ф'(x))
=
m⇒
такие
числа
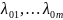 , что точка
,
, что точка
,
 является стационарной точкой функции
Лагранжа.
является стационарной точкой функции
Лагранжа.
Условный экстремум функции 2-ух переменных.
Экстремум
функции
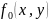 при условии
при условии
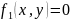 .
.
1)Строим функцию Лагранжа и находим ее стационарные точки.
L
(x, y,
)=
+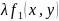
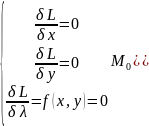 ,
и
,
и
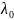 .
.
2)Находим 2 фиксированные функции L в .
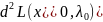 =
=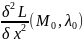 (
(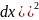 +2
+2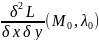 dx
dy +
dx
dy +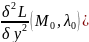 .
.
3)Находим
связь dx
и
dy
в
с помощью дифф. от уравнения связи
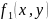 =0⇐
=0⇐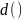
dy=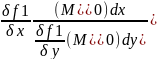 Е=
{(
dx,
dy):
Е=
{(
dx,
dy):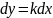 }
}
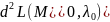 заменяем
и получаем
заменяем
и получаем