21.Понятие транспортной задачи и условие оптимальности плана распределения перевозок

Пусть имеется некоторый однородный продукт, сосредоточенный на m пунктах отправления (складах), так что на i-м складе находится ai единиц этого продукта.Этот продукт необходимо доставить в n пунктов назначения (потребления), причем на j-й пункт необходимо доставить bj единиц продукта. Запасы ипотребности сбалансированы, то есть

,то есть наличие продукта равно потребности в нем.Пусть стоимость перевозки единицы продукта из i-го склада в j-й пункт назначения равна . Пусть есть то количество продукта, которое перевозится из i-го склада в j-й пункт потребления.Тогда общие транспортные расходы составят величину Из каждого склада весь продукт должен быть вывезен. Это значит, что должно быть выполнено условие

С другой стороны, потребности j-го пункта назначения должны быть полностью удовлетворены. Это означает, что

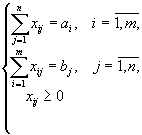Желание минимизировать транспортные расходы приводит нас к следующей задаче: являющейся типичной задачей линейного программирования/ Транспортная задача называется открытой транспортной задачей, если условие баланса нарушаются; в случае выполнения условия баланса она называется сбалансированной транспортной задачей.Однако у этой задачи есть одна очень существенная особенность: в ограничениях перед неизвестными всегда стоит 1. И именно это позволяет разработать гораздо более эффективные и простые алгоритмы решения транспортной задачи, чем симплекс-метод.Сам же симплекс-метод был бы не эффективен по двум причинам:Большая размерность решаемой задачи. Общее число неизвестных величин равно mn , и даже при n =m = 10 размерность решаемой задачи уже будет равна 100. Даже ЭВМ будет решать такую задачу симплекс-методом достаточно долго. Опорные планы в транспортной задаче очень часто бывают вырожденными, а наличие вырождения приводит к необходимости несколько модифицировать симплекс-метод. Чтобы оценить оптимальность распределения, для всех свободных клеток (i;j) матрицы перевозок определяются их оценки, которые обозначим

через по формуле: = с – (u + v )

ks ks ij i j

Очевидно, оценки заполненных клеток равны нулю. Таким образом, об оптимальности распределения можно судить по величинам оценок свободных клеток. Если оценка некоторой свободной клетки отрицательна, то это можно интерпретировать так: если бы эта клетка была занята, то можно было бы получить дополнительный экономический эффект. Следовательно, условием оптимальности распределения служит условие неотрицательности оценоксвободныхклетокматрицы перевозок.

= с – (u + v ) ≥ 0 (6.13.)

ks ij i j

22.Понятие и основные формулы расчета финансовой ренты в моделях финансово-коммерческих операциях

В финансовой литературе ряд распределенных во времени выплат и поступлений называется потоком платежей.Потоки платежей являются неотъемлемой частью всевозможных финансовых операций: с ценными бумагами, в управлении финансами предприятий, при осуществлении инвестиционных проектов, в кредитных операциях, при оценке бизнеса, при оценке недвижимости, выборе альтернативных вариантов финансовых операций и т. п.Члены потока могут быть как положительными величинами (поступления), так и отрицательными величинами (выплатами), а временные интервалы между членами такого потока могут быть равными и неравными.Поток платежей, все члены которого имеют одинаковое направление (знак), а временные интервалы между последовательными платежами постоянны, называется финансовой рентой или аннуитетом.При рассмотрении финансовой ренты используются основные категории:член ренты (R) – величина каждого отдельного платежа; период ренты (t) – временной интервал между членами ренты; срок ренты (n) – время от начала финансовой ренты до конца последнего ее периода; процентная ставка (i) – ставка, используемая при наращении платежей, из которых состоит рента. Поскольку условия финансовых сделок весьма разнообразны, постольку разнообразны и виды потоков платежей. Финансовая рента (аннуитет) – поток одинаковых платежей, все элементы которых положительные величины, а временные интервалы между платежами - одинаковы.Характеристики ренты:Размер платежа (Payment – PMT);Период ренты;Срок ренты;Процентная ставка.