25. Моделирование броуновского движения частицы;

Бро́уновское движе́ние — в естествознании, беспорядочное движение микроскопических, видимых, взвешенных в жидкости (или газе) частиц твёрдого вещества (пылинки, частички пыльцы растения и так далее), вызываемое тепловым движением частиц жидкости (или газа). Не следует смешивать понятия «броуновское движение» и «тепловое движение»: броуновское движение является следствием и свидетельством существования теплового движения.

В математике, а точнее в теории случайных процессов, броуновское движение (или винеровский процесс*) — это гауссовский процесс с независимыми приращениями, у которого математическое ожидание равно нулю, а среднеквадратическое отклонение равно  .

Сущность явления

Броуновское движение происходит из-за того, что все жидкости и газы состоят из атомов или молекул — мельчайших частиц, которые находятся в постоянном хаотическом тепловом движении, и потому непрерывно толкают броуновскую частицу с разных сторон. Было установлено, что крупные частицы с размерами более 5 мкм в броуновском движении практически не участвуют (они неподвижны или седиментируют), более мелкие частицы (менее 3 мкм) двигаются поступательно по весьма сложным траекториям или вращаются. Когда в среду погружено крупное тело, то толчки, происходящие в огромном количестве, усредняются и формируют постоянное давление. Если крупное тело окружено средой со всех сторон, то давление практически уравновешивается, остаётся только подъёмная сила Архимеда — такое тело плавно всплывает или тонет. Если же тело мелкое, как броуновская частица, то становятся заметны флуктуации давления, которые создают заметную случайно изменяющуюся силу, приводящую к колебаниям частицы. Броуновские частицы обычно не тонут и не всплывают, а находятся в среде во взвешенном состоянии.

Теория броуновского движения Построение классической теории

В 1905 году Альбертом Эйнштейном была создана молекулярно-кинетическая теория для количественного описания броуновского движения. В частности, он вывел формулу для коэффициента диффузии сферических броуновских частиц^[3]:

где   — коэффициент диффузии,   — универсальная газовая постоянная,   — абсолютная температура,   — постоянная Авогадро,   — радиус частиц,   — динамическая вязкость.

Экспериментальное подтверждение

Формула Эйнштейна была подтверждена опытами Жана Перрена и его студентов в 1908-1909 гг. В качестве броуновских частиц они использовали зёрнышки смолы мастикового дерева и гуммигута — густого млечного сока деревьев рода гарциния. Справедливость формулы была установлена для различных размеров частиц — от 0,212 мкм до 5,5 мкм, для различных растворов (раствор сахара, глицерин), в которых двигались частицы.

Броуновское движение как немарковский случайный процесс

Хорошо разработанная за последнее столетие теория броуновского движения является приближенной. И хотя в большинстве практически важных случаев существующая теория даёт удовлетворительные результаты, в некоторых случаях она может потребовать уточнения. Так, экспериментальные работы, проведённые в начале XXI века в Политехническом университете Лозанны, Университете Техаса и Европейской молекулярно-биологической лаборатории в Гейдельберге (под руководством С. Дженей) показали отличие поведения броуновской частицы от теоретически предсказываемого теорией Эйнштейна — Смолуховского, что было особенно заметным при увеличении размеров частиц. Исследования затрагивали также анализ движения окружающих частиц среды и показали существенное взаимное влияние движения броуновской частицы и вызываемое ею движение частиц среды друг на друга, то есть наличие «памяти» у броуновской частицы, или, другими словами, зависимость её статистических характеристик в будущем от всей предыстории её поведения в прошлом. Данный факт не учитывался в теории Эйнштейна — Смолуховского.

Процесс броуновского движения частицы в вязкой среде, вообще говоря, относится к классу немарковских процессов, и для более точного его описания необходимо использование интегральных стохастических уравнений.

*Винеровский процесс в теории случайных процессов — это математическая модель броуновского движения или случайного блуждания с непрерывным временем.

Определение

Случайный процесс   называется винеровским процессом, если

1.  почти наверное.

2.  — процесс с независимыми приращениями.

3. , для любых  , где   обозначает нормальное распределение со средним   и дисперсией 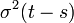 . Величина   является постоянной для данного процесса.

Физический смысл

Винеровский процесс описывает броуновское движение частицы, совершающей беспорядочные перемещения под влиянием ударов молекул жидкости. Константа   при этом зависит от массы частицы и вязкости жидкости.

Непрерывность траекторий

Существуют винеровские процессы такие, что почти все их траектории непрерывны. Часто непрерывность траекторий включается в определение винеровского процесса.

Свойства винеровского процесса

•  — гауссовский процесс.

•  — марковский процесс.

• Очевидно,  . В частности:

,

.

• .

• Винеровский процесс автомоделен. Если   — винеровский процесс, и 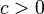 , то

также является винеровским процессом.

• Корреляционная функция для производной винеровского процесса является дельта-функцией.

• Траектории винеровского процесса нигде не дифференцируемы почти наверное. Производная (в обобщенном смысле) винеровского процесса - нормальный белый шум.

• Для любого заданного отрезка траектории винеровского процесса — функции неограниченной вариации на этом отрезке почти наверное

•