Имитационное моделирование разброса сопротивлений в партии резисторов;
Моделирование игры в кости;
Есть работа в маткаде на эту тему.
Моделирование доски Гальтона;
Доска́ Га́льтона (англ. Galton box, также распространены названия квинкункс, quincunx и bean machine) — устройство, изобретённое английским учёным Фрэнсисом Гальтоном (первый экземпляр изготовлен в 1873 году[1], затем устройство было описано Гальтоном в книге Natural inheritance, изданной в 1889 году) и предназначающееся для демонстрации центральной предельной теоремы.
Устройство
Доска Гальтона представляет собой ящик с прозрачной передней стенкой. В заднюю стенку в шахматном порядке вбиты штырьки, образующие треугольник. Сверху в ящик через воронку (выход из которой расположен ровно посередине между левой и правой стенками) кидаются шарики. В идеальном случае сталкиваясь со штырьком, шарик каждый раз с одинаковой вероятностью может повернуть либо направо, либо налево. Нижняя часть ящика разделена перегородками (число которых равно числу штырьков в нижнем ряду), в результате чего шарики, скатываясь на дно ящика, образуют столбики, которые тем выше, чем ближе к середине доски (при достаточно большом числе шариков внешний вид столбиков приближается к кривой нормального распределения).
Если нарисовать на задней стенке треугольник Паскаля, то можно увидеть, сколькими путями можно добраться до каждого из штырьков (чем ближе штырёк к центру, тем больше число путей).
В некоторых настольных играх, а также игровом автомате Патинко, используется доска Гальтона или схожие с ней устройства.
Распределение шариков
Обозначим
как n общее
число столкновений шарика со штырьками;
как k число
раз, когда шарик поворачивает направо
(таким образом, он оказывается в k-м
по порядку столбике). Тогда число
способов, которыми он может добраться
доk-го
столбика, определяется биномиальным
коэффициентом* 
.
Отсюда следует, что вероятность оказаться
в k-м
столбике равна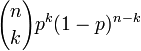 
,
где p —
вероятность поворота направо (обычно
можно считать, что 
).
Это функция
вероятности биномиального
распределения,
которое в соответствии с центральной
предельной теоремой при достаточно
большом n аппроксимирует нормальное
распределение**.
*
В математике биномиальные
коэффициенты —
это коэффициенты в разложении бинома
Ньютона 
по
степеням x.
Коэффициент при 
обозначается 
(иногда 
)
и читается «биномиальный коэффициент
из n по k»
(или «це из n по k»):
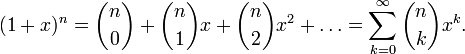
В комбинаторике(раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения и перечисления элементов) и отношения на них) биномиальный коэффициент интерпретируется как количество сочетаний из n по k, то есть количество всех подмножеств (выборок) размера k в n-элементном множестве.
** Нормальное распределение, также называемое гауссовым распределением или распределением Гаусса — распределение вероятностей, которое задается функцией плотности распределения:
где параметр μ — среднее значение (математическое ожидание) случайной величины и указывает координату максимума кривой плотности распределения, а σ² — дисперсия.
Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием 0 и стандартным отклонением 1.