
- •Теория вероятностей.
- •Пространство элементарных исходов.
- •Вероятность на дискретном пространстве элементарных исходов.
- •Классическое определение вероятности
- •Сигма-алгебра событий.
- •Определение вероятности на общем пространстве элементарных исходов. Свойства вероятности.
- •Геометрические вероятности. Примеры.
- •Условная вероятность
- •Независимость событий в совокупности
- •Формула полной вероятности.
- •Последовательность испытаний Бернулли.
- •Теорема Пуассона.
- •Случайные величины. Определение. Функция распределения случайной величины и её свойства.
- •Дискретные случайные величины. Примеры распределения дискретных случайных величин.
- •Абсолютно непрерывные распределения случайных величин. Плотность распределения и её свойства.
- •Примеры абсолютно непрерывных распределений. Равномерное распределение
- •Совместная функция распределения двух случайных величин и её свойства. Совместное распределение двух дискретных случайных величин.
- •Абсолютно непрерывные совместные распределения двух случайных величин. Совместная плотность распределения, её свойства.
- •Условные плотности распределения.
- •Распределения n-мерных случайных векторов. Дискретные распределения, абсолютно непрерывные распределения.
- •Распределение функции от случайной величины. Примеры.
- •Независимость случайных величин.
- •Распределение суммы независимых случайных величин. Формула свертки.
- •Математическое ожидание случайных величин. Свойства математического ожидания. Примеры.
- •Дисперсия случайных величин. Свойства дисперсии. Примеры.
- •Ковариация. Свойства.
- •Коэффициент корреляции. Свойства.
- •Двумерное нормальное распределение и его параметры.
- •Неравенство Маркова. Неравенство Чебышева.
- •Сходимость по вероятности последовательности случайных величин. Свойства сходимости по вероятности.
- •Закон больших чисел.
- •Слабая сходимость последовательности случайных величин и её свойства.
- •Соотношения между слабой сходимостью случайных величин и сходимостью по вероятности.
- •Центральная предельная теорема. Различные формулировки центральной предельной теоремы.
Дисперсия случайных величин. Свойства дисперсии. Примеры.
Дисперсией
случайной величины
называют математическое ожидание
квадрата отклонения случайной величины
от ее математического ожидания:
![]()
Дисперсию
удобно вычислять по формуле:
![]()
Свойства дисперсии:
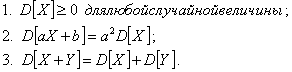
Ковариация. Свойства.
Мы знаем, что для независимых случайных величин с конечными вторыми моментами дисперсия их суммы равна сумме их дисперсий. В общем случае, согласно следствию 16, дисперсия суммы равна
|
(19) |
Величина
![]() равняется
нулю, если случайные величины
и
независимы
(свойство (E7)
математического ожидания). С другой
стороны, из равенства её нулю вовсе не
следует независимость, как показывают
примеры 34
и 35.
Эту величину часто используют как
«индикатор наличия зависимости»
между двумя случайными
величинами.
равняется
нулю, если случайные величины
и
независимы
(свойство (E7)
математического ожидания). С другой
стороны, из равенства её нулю вовсе не
следует независимость, как показывают
примеры 34
и 35.
Эту величину часто используют как
«индикатор наличия зависимости»
между двумя случайными
величинами.
Определение.
Ковариацией
![]() случайных
величин
и
называется
число
случайных
величин
и
называется
число
![]()
Коэффициент корреляции. Свойства.
Определение.
Коэффициентом
корреляции
![]() случайных
величин
и
,
дисперсии
которых существуют
и отличны
от нуля,
называется число
случайных
величин
и
,
дисперсии
которых существуют
и отличны
от нуля,
называется число
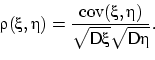
Замечание. Чтобы разглядеть «устройство» коэффициента корреляции, распишем по определению числитель и знаменатель:
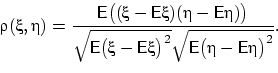
Коэффициент корреляции обладает свойствами:
1)
если
и
независимы,
то
![]() ;
;
2)
всегда
![]() ;
;
3)
![]() тогда и только тогда, когда
и
п. н.
линейно связаны, т.е. существуют числа
тогда и только тогда, когда
и
п. н.
линейно связаны, т.е. существуют числа
![]() и
и
![]() такие,
что
такие,
что
![]() .
.
Двумерное нормальное распределение и его параметры.
Двумерный
случайный
вектор
![]() имеет
нормальное
распределение, если его плотность
равна
имеет
нормальное
распределение, если его плотность
равна
![]()
где
![]()
— вектор математических ожиданий,
![]()
— ковариационная матрица.
Плотность двумерного нормального распределения записывается также в виде
![]()
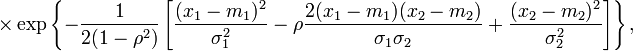
где
![]()
— определитель ковариационной матрицы,
![]()
— коэффициент
корреляции случайных
величин
![]() и
и
![]() .
.
Неравенство Маркова. Неравенство Чебышева.
Теорема
(неравенство Маркова). Если
,
то для любого
![]()
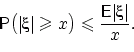
Доказательство. Нам потребуется следующее понятие.
Определение.
Пусть
—
некоторое событие. Назовём индикатором
события
случайную
величину
![]() ,
равную единице, если событие
произошло,
и нулю, если
не
произошло.
,
равную единице, если событие
произошло,
и нулю, если
не
произошло.
По
определению, величина
имеет
распределение
Бернулли с параметром
![]() ,
и её математическое
ожидание равно вероятности успеха
,
и её математическое
ожидание равно вероятности успеха
![]() .
Индикаторы прямого и противоположного
событий связаны равенством
.
Индикаторы прямого и противоположного
событий связаны равенством
![]() .
Поэтому
.
Поэтому
![]()
Тогда
|
(21) |
Осталось разделить обе части неравенства (21) на положительное .
Следующее неравенство мы будем называть обобщённым неравенством Чебышёва.
Следствие
(обобщённое
неравенство Чебышёва). Пусть
функция
![]() не
убывает и неотрицательна на
.
Если
,
то для любого
не
убывает и неотрицательна на
.
Если
,
то для любого
![]()
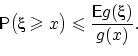
Доказательство.
Заметим,
что
![]() ,
поскольку функция
не
убывает. Оценим последнюю вероятность
согласно неравенству
Маркова, которое можно применять в
силу неотрицательности
:
,
поскольку функция
не
убывает. Оценим последнюю вероятность
согласно неравенству
Маркова, которое можно применять в
силу неотрицательности
:
![]()
Сходимость по вероятности последовательности случайных величин. Свойства сходимости по вероятности.
Говорят,
что последовательность случайных
величин
![]() сходится
по вероятности к случайной величине
сходится
по вероятности к случайной величине
![]() при
при
![]() ,
и пишут
,
и пишут
![]() ,
если для любого
,
если для любого
![]()
![]()
Пример.
Рассмотрим
последовательность
![]() ,
в которой все величины имеют разные
распределения: величина
,
в которой все величины имеют разные
распределения: величина
![]() принимает
значения
принимает
значения
![]() и
и
![]() с
вероятностями
с
вероятностями
![]() .
Докажем, что эта последовательность
сходится по вероятности к нулю.
.
Докажем, что эта последовательность
сходится по вероятности к нулю.
Зафиксируем
произвольное
.
Для всех
![]() начиная
с некоторого
начиная
с некоторого
![]() такого,
что
такого,
что
![]() ,
верно равенство
,
верно равенство
![]() .
Поэтому
.
Поэтому
![]()
Итак, случайные величины с ростом могут принимать все большие и большие значения, но со все меньшей и меньшей вероятностью.
Например,
последовательность
можно
задать на вероятностном пространстве
![]() так:
положим
так:
положим
![]() для
для
![]() и
и
![]() для
для
![]() .
.
Свойства:
(![]() и
и
![]() )
)
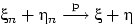 ;
;
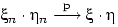 .
.
Если и
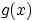 —
непрерывная функция, то
—
непрерывная функция, то
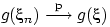 .
.
Если
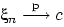 и
непрерывна
в точке
,
то
и
непрерывна
в точке
,
то
 .
.
