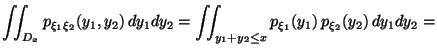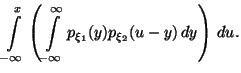21. Независимость случайных величин.

Определение. Пусть дано семейство случайных величин , так что . Тогда эти случайные величины попарно независимы, если попарно независимы порождённые ими сигма-алгебры . Случайные величины независимы в совокупности, если таковы порождённые ими сигма-алгебры.

Определение, данное выше, эквивалентно любому другому из нижеперечисленных. Две случайные величины независимы тогда и только тогда, когда:

1. Для любых :

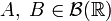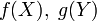2. Для любых борелевских функций случайные величины независимы.

3. Для любых ограниченных борелевских функций :

Свойства независимых случайных величин

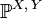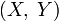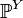1. Пусть  — распределение случайного вектора ,  — распределение и  — распределение . Тогда независимы тогда и только тогда, когда

где обозначает (прямое) произведение мер.

2. Пусть 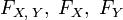 — кумулятивные функции распределения 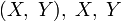соответственно. Тогда независимы тогда и только тогда, когда

3. Пусть случайные величины дискретны. Тогда они независимы тогда и только тогда, когда

4. Пусть случайные величины совместно абсолютно непрерывны, то есть их совместное распределение имеет плотность 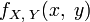. Тогда они независимы тогда и только тогда, когда

,

где  — плотности случайных величин и соответственно.

22. Распределение суммы независимых случайных величин. Формула свертки.

Многие важные случайные величины представляются в виде сумм независимых слагаемых. Нижеследующее утверждение устанавливает, как распределение суммы связано с распределениями слагаемых.

Пусть с.в. и абсолютно непрерывны с плотностями и и независимы. Тогда

(25)

Доказательство. Пусть .

		замена

Так как это равенство выполнено при всех , то из определения плотности распределения получаем формулу свертки.

23. Математическое ожидание случайных величин. Свойства математического ожидания. Примеры.

Определение. Математическим ожиданием (средним значением, первым моментом) случайной величины с дискретным распределением, задаваемым таблицей , где , называется число

если данный ряд абсолютно сходится, т.е. если . В противном случае говорят, что математическое ожидание не существует.

Определение. Математическим ожиданием (средним значением, первым моментом) случайной величины с абсолютно непрерывным распределением с плотностью распределения называется число

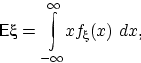
если этот интеграл абсолютно сходится, т.е. если 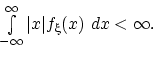  В противном случае математическое ожидание не существует.

Математическое ожидание имеет простой физический смысл: если на прямой разместить единичную массу, поместив в точки массу (для дискретного распределения), или «размазав» её с плотностью (для абсолютно непрерывного распределения), то точка будет координатой «центра тяжести» прямой.

Свойства. Во всех свойствах предполагается, что рассматриваемые математические ожидания существуют.

E1. Для произвольной борелевской функции

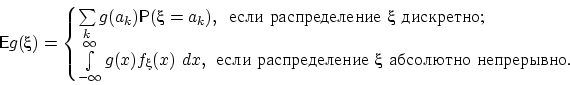
Доказательство. Мы докажем это свойство (как и почти все дальнейшие) только для дискретного распределения. Пусть принимает значения с вероятностями

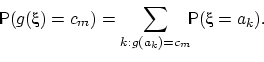
Тогда

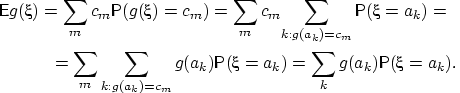
Следствие. Математическое ожидание существует тогда и только тогда, когда .

Доказательство. Условием существование математического ожидания является абсолютная сходимость ряда или интеграла в определениях 42 и 43. По свойству (E1) это и есть условие при .

E2. Математическое ожидание постоянной равно ей самой: .

E3. Постоянную можно вынести за знак математического ожидания:

Доказательство следует из свойства (E1) при .

E4. Математическое ожидание суммы любых случайных величин равно сумме их математических ожиданий, если только эти математические ожидания существуют:

Доказательство. Пусть случайные величины и имеют дискретные распределения со значениями и соответственно. Для борелевской функции можно доказать свойство, аналогичное (E1) (сделать это!). Воспользуемся этим свойством для :

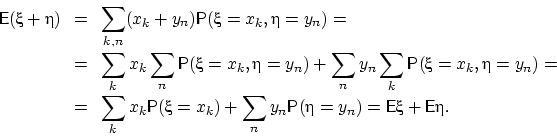
E5. Если п.н., т.е. если , то .

E6. Если п.н., и при этом , то п.н., т.е. .

Доказательство. Это свойство мы докажем, заранее предполагая, что имеет дискретное распределение с неотрицательными значениями . Равенство означает, что все слагаемые в этой сумме равны нулю, т.е. все вероятности нулевые, кроме вероятности, соответствующей значению .

Из свойств (E5) и (E6) вытекает множество полезных утверждений:

Следствие. Если п.н., то .

Следствие. Если п.н., но , то п.н.

Следствие. Если п.н., то .

E7. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий: если и независимы и их математические ожидания существуют, то

Доказательство. В дискретном случае:

Замечание. Обратное утверждение к свойству (E7) неверно: из равенства не следует независимость величин и .

Пример. Пусть принимает значения 0 и с вероятностями по 1/3 каждое, и . Это зависимые случайные величины:

Однако и , поэтому .

Пример. Пусть , и пусть и  — заведомо зависимые случайные величины (доказать!). Но математическое ожидание их произведения равно произведению их математических ожиданий из-за симметричности распределений , и относительно нуля. Действительно, по свойству (E1) имеем:

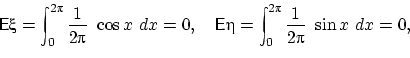
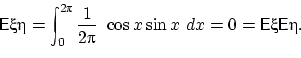
Пример. Пусть случайная величина равна числу очков, выпадающих при одном подбрасывании кубика. Тогда

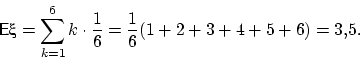
В среднем при одном подбрасывании кубика выпадает 3,5 очка.

Пример. Пусть случайная величина — координата точки, брошенной наудачу на отрезок . Тогда