9. Формула полной вероятности.

Пример. Есть три завода, производящих одну и ту же продукцию. При этом первый завод производит 25%, второй завод — 35% и третий — 40% всей производимой продукции. Брак составляет 5% от продукции первого завода, 3% от продукции второго и 4% от продукции третьего завода. Вся продукция смешивается и поступает в продажу. Найти а) вероятность купить бракованное изделие; б) условную вероятность того, что купленное изделие изготовлено первым заводом, если это изделие бракованное.

Первая вероятность равна доле бракованных изделий в объеме всей продукции, т.е. . Вторая вероятность равна доле брака первого завода среди всего брака, т.е.

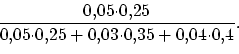
Заметим, что найти эти вероятности можно безо всякого знания теории вероятностей вообще. Достаточно элементарного здравого смысла.

Теорема (формула полной вероятности). Пусть — полная группа событий. Тогда вероятность любого события может быть вычислена по формуле:

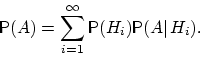
p (А) = p (А | Н₁) p (Н ₁) + p (А | Н ₂) p (Н ₂) + p (А | Н ₃) p (Н ₃) +… + p (А | Н _k) p (Н _k)

Доказательство. Заметим, что

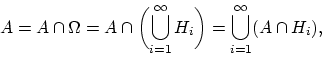
и события , попарно несовместны. Поэтому

Теорема (формула Байеса). Пусть — полная группа событий, и — некоторое событие, вероятность которого положительна. Тогда условная вероятность того, что имело место событие , если в результате эксперимента наблюдалось событие , может быть вычислена по формуле:

Доказательство. По определению условной вероятности,

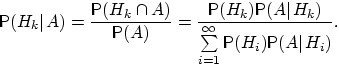
Пример. Вернёмся к примеру 21. Изделие выбирается наудачу из всей произведённой продукции. Рассмотрим три гипотезы: , . Вероятности этих событий даны: , , .

Пусть . Даны также условные вероятности , , .

Пример. Два стрелка подбрасывают монетку и выбирают, кто из них стреляет по мишени (одной пулей). Первый стрелок попадает по мишени с вероятностью 1, второй стрелок — с вероятностью 0,00001. Можно сделать два предположения об эксперименте: и . Априорные (a'priori — «до опыта») вероятности этих гипотез одинаковы: .

Рассмотрим событие . Известно, что

Поэтому вероятность пуле попасть в мишень

Предположим, что событие произошло. Какова теперь апостериорная (a'posteriori — «после опыта») вероятность каждой из гипотез ? Очевидно, что первая из этих гипотез много вероятнее второй (а именно, в  раз). Действительно,

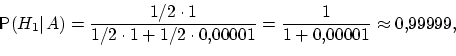
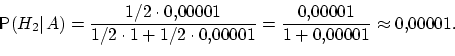
10. Последовательность испытаний Бернулли.

Пусть выполняется некоторый эксперимент (испытание) 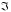. В результате этого эксперимента происходит событие 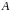с вероятностью 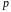. Если событие произошло, то говорят, что результатом испытания был “успех” , а в противном случае, говорят, что в результате испытания имела место “неудача”. Вероятность “неудачи” обозначают 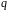. Ясно, что 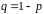. Казалось бы, это бедная модель, но на самом деле, она обслуживает большое число ситуаций. Например, успел – не успел, выбрали – не выбрали, сдал экзамен – не сдал экзамен и т.п.

Если имеются такие условия, что испытание может повторяться неограниченное число раз с неизменной вероятностью “успеха” , причём, исход следующего испытания не зависит от исходов предыдущих испытаний, то говорят, что рассматривается последовательность испытаний Бернулли. Иногда, подчёркивая независимость последовательных испытаний, говорят – последовательность независимых испытаний Бернулли.

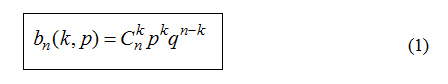
Пример. Некоторый гражданин выходит из дома за час до начала работы. При этом, вероятность того, что он опоздает на работу равна 0.1. Какова вероятность того, что гражданин в течение недели он опоздает на работу два раза.

Решение. В неделе, считаем, 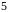дней. Причем, опоздание в текущий день не зависит от опозданий в другие дни. Вероятность опоздания не меняется в зависимости от дня недели. Значит, в этой задаче мы имеем дело с последовательностью испытаний Бернулли. Успех, при такой формулировке задачи, – это опоздание. Вероятность двух успехов в испытаниях Бернулли с вероятностью успеха 0,1 вычисляется по формуле

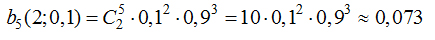
Наиболее вероятное число успехов.

Проанализируем формулу (1) вероятности 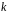успехов в последовательности 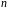испытаний Бернулли. Для этого рассмотрим отношение