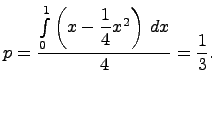Сигма-алгебра событий.

В теории вероятностей часто возникает необходимость объединять счётные наборы событий и считать событием результат такого объединения. При этом свойства (A3) алгебры оказывается недостаточно: из него не вытекает, что объединение счётной последовательности множеств из алгебры снова принадлежит алгебре. Поэтому разумно наложить более суровые ограничения на класс событий.

Множество , элементами которого являются подмножества множества (не обязательно все) называется -алгеброй ( -алгеброй событий), если выполнены следующие условия:

(S1)      ( -алгебра событий содержит достоверное событие);

(S2)  если , то (вместе с любым событием -алгебра содержит противоположное событие);

(S3)  если ,  , то (вместе с любым счётным набором событий -алгебра содержит их объединение).

Свойство 2. Свойство (S3) можно заменить на

(S4)  если ,  , то .

Как показывает следующее свойство, всякая -алгебра автоматически является алгеброй.

Свойство 3. Если — -алгебра, то она удовлетворяет свойству (A3), т.е. для любых и выполняется .

Доказательство. Превратим пару в счётную последовательность событий так: , т.е. положим , при всех . Объединение совпадает с объединением всех множеств из этой бесконечной последовательности. А так как  — -алгебра, то

Пример. Пусть , и пусть — множество, содержащее любые конечные подмножества (т.е. состоящие из конечного числа точек, в том числе пустое) и их дополнения. В частности, множество принадлежит , множество также принадлежит  .

Легко проверить, что множество является алгеброй. Действительно, пустое множество и само там содержатся, дополнение к любому конечному подмножеству множества вещественных чисел содержится в по определению, дополнение к множеству вида для конечных совпадает с и также принадлежит по определению. Свойство (A3) проверяется непосредственно: объединение любых конечных множеств снова конечно и поэтому принадлежит . Объединение конечного множества с множеством вида , где конечно, есть снова множество вида , где конечно (или пусто). Объединение двух множеств и , являющихся дополнениями до конечных множеств и , есть снова множество такого же вида.

Однако алгебра не содержит ни одного счётного множества точек. Действительно, объединяя конечные множества в конечном числе, мы можем получить только конечное множество. Например, натуральный ряд не принадлежит . Поэтому не является -алгеброй: для бесконечной, но счётной последовательности одноточечных множеств из их объединение не принадлежит  .

Все алгебры из примера 11 являются -алгебрами, поскольку содержат лишь конечное число элементов. Вообще, на конечном множестве понятия алгебры и -алгебры совпадают. Множество всех подмножеств является -алгеброй для любого .

5. Определение вероятности на общем пространстве элементарных исходов. Свойства вероятности.

6. Геометрические вероятности. Примеры.

При геометрическом подходе к определению вероятности в качестве пространства элементарных событий рассматривается произвольное множество конечной лебеговой меры на прямой, плоскости или пространстве. Событиями называются всевозможные измеримые подмножества множества .

Вероятность события А определяется формулой

где обозначает лебегову меру множества А. При таком определении событий и вероятностей все аксиомы А.Н.Колмогорова выполняются.

В конкретных задачах, которые сводятся к указанной выше вероятностной схеме, испытание интерпретируется как случайный выбор точки в некоторой области , а событие А – как попадание выбранной точки в некоторую подобласть А области . При этом требуется, чтобы все точки области имели одинаковую возможность быть выбранными. Это требование обычно выражается словами «наудачу», «случайным образом» и т.д.

Пример. В круг радиуса R наудачу брошена точка. Найдите вероятность того, что эта точка окажется внутри данного вписанного правильного треугольника.

Искомая вероятность равна отношению площади треугольника к площади круга:

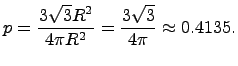
Пример. Из отрезка [0, 2] на удачу выбраны два числа х и у. Найдите вероятность того, что эти числа удовлетворяют неравенствам .

По условиям опыта координаты точки (х,у) удовлетворяют системе неравенств:

Это значит, что точка (х,у) наудачу выбирается из множества точек квадрата со стороной 2. Интересующее нас событие происходит в том и только в том случае, когда выбранная точка (х,у) окажется под прямой и над параболой. Эта область получена как множество точек, ординаты которых удовлетворяют неравенствам Следовательно, искомая вероятность равна отношению площади области к площади квадрата: