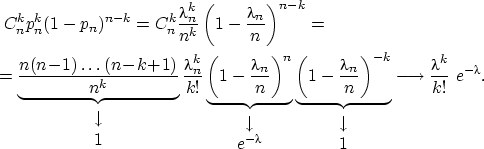11. Теорема Пуассона.

Пусть и так, что . Тогда для любого вероятность получить успехов в  испытаниях схемы Бернулли с вероятностью успеха стремится к величине

Доказательство. Положим . Тогда  и

(8)

В соотношении (8) мы воспользовались тем, что и замечательным пределом . Докажем последнее свойство:

12. Случайные величины. Определение. Функция распределения случайной величины и её свойства.

Функцией распределения называют функцию Р (х), определяющую для каждого значения х вероятность того, что случайная величина Х примет значение, меньшее х, т. е.

F(х)=Р(Х<х).

Часто вместо термина «функция распределения» используют термин «интегральный закон распределения».

Функция распределения обладает следующими свойствами:

Для непрерывной случайной величины выполняется следующее свойство, называемое иногда «парадоксом нулевой вероятности»: P(X=a)=0 для любого конкретного числа а.

13. Дискретные случайные величины. Примеры распределения дискретных случайных величин.

Биномиальное распределение

Дискретная случайная величина X, принимающая целочисленные значения имеет биномиальное распределение, если вероятность значения k вычисляется по формуле Бернулли:

где 0<p<1, q=1-p.

Биномиальный закон распределения имеет случайная величина, равная числу успехов в серии из n независимых испытаний Бернулли с вероятностью успеха p в каждом испытании.

Для биномиального распределения

Распределение Пуассона

Дискретная случайная величина X, принимающая положительные целочисленные значения k , имеет распределене Пуассона, если вероятности ее значений вычисляются по формуле

Для распределения Пуассона

Теорема Пуассона.

Эта теоре­ма дает пуассоновское приближение биномиального распределения и обычно используется при p<0,1 и npq 9 .

Равномерное распределение

Непрерывная случайная величина X, принимающая значения на отрезке имеет равномерное распределение, если плотность распределения вероятностей имеет вид

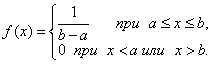
14. Абсолютно непрерывные распределения случайных величин. Плотность распределения и её свойства.

Cлучайная величина имеет абсолютно непрерывное распределение, если существует неотрицательная функция такая, что для любого борелевского множества имеет место равенство:

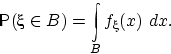
Функцию называют плотностью распределения случайной величины  .

Теорема. Плотность распределения обладает свойствами:

 (f1)    для любого ;      (f2)    .

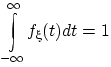Плотностью распределения вероятностей непрерывной случайной величины называют первую производную от функции распределения:

Вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу , определяется равенством:

Зная плотность распределения, можно найти функцию распределения

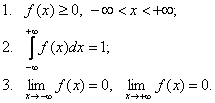
15. Примеры абсолютно непрерывных распределений. Равномерное распределение

Говорят, что имеет равномерное распределение на отрезке , и пишут: , если плотность распределения постоянна на отрезке и равна нулю вне него:

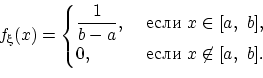
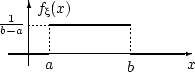
Очевидно, что площадь под графиком этой функции равна единице и  . Поэтому  является плотностью распределения.

Случайная величина имеет смысл координаты точки, выбранной наудачу на отрезке . Вычислим по определению 30 функцию распределения случайной величины :

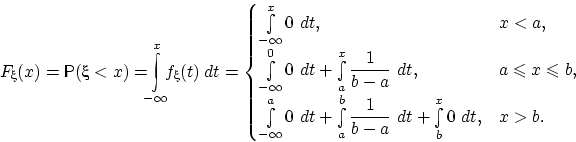
Получим следующую непрерывную функцию распределения:

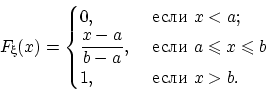
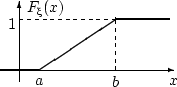
Нормальное распределение.

Для нормального распределения

Вероятность попадания нормально распределенной случайной величины на отрезок вычисляется по формуле

где Ф(х) – функция Лапласа, которая определяется равенством

Интегральная теорема Муавра – Лапласа

Если то для случайной величины X

Теорема дает нормальное приближение биномиального распределения применяется при p>0,1 и npq>9.

Показательное распределение

Говорят, что имеет показательное (экспоненциальное) распределение с параметром , и пишут: , если имеет следующую плотность распределения:

   

Функция распределения случайной величины непрерывна:

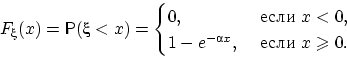
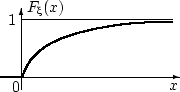
Показательное распределение является единственным абсолютно непрерывным распределением, для которого выполнено свойство «нестарения» (и в этом смысле оно является непрерывным аналогом дискретного геометрического распределения).

Гамма-распределение

Говорят, что имеет гамма-распределение с параметрами , , и пишут: , если имеет следующую плотность распределения:

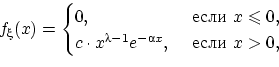
где постоянная вычисляется из свойства (f2) плотности так:

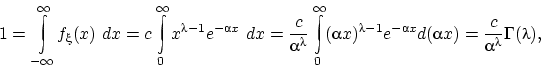
откуда . Здесь через обозначен интеграл

называемый гамма-функцией Эйлера; при целых положительных , . Замена в интеграле Пуассона даст .

Показательное распределение — частный случай гамма-распределения: .

Функцию распределения гамма-распределения можно записать, вообще говоря, только в виде интеграла:

Но при целых значениях параметра интегрированием по частям этот интеграл можно превратить в сумму: