
- •1.Решения
- •1. Решение на числовом промежутке
- •2. Задача Коши
- •3. Продолжение решений.
- •4. Общее решение.
- •5. Интегральная поверхность
- •6. Интегральная кривая, заданная неявно
- •7. Первый интеграл
- •8. Базис первых интегралов
- •2.Траектории
- •1. Траектория
- •3. Регулярные точки
- •4. Виды траекторий
- •5. Параметрическое задание траекторий
- •6. Неявное задание траекторий
- •7. Уравнение траекторий
- •7.Сложные состояния равновесия систем с линейными членами.
- •8. Признаки ограниченности числа предельных циклов.
- •10.Преобразование Бендиксона
- •13. Преобразование Пуанкаре.2
- •14. Круг Пуанкаре.
- •15. Типы диф. Сис-мы на проективной ф.П.
- •16. Поведение траекторий в окрестности экватора сферы Пуанкаре (s2 p)
- •17. Проективный атлас сферы Пуанкаре.
7.Сложные состояния равновесия систем с линейными членами.
Пусть состояние равновесия (СР) О(0,0) системы
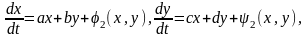 (1)
где
числа a,
b,
c
и
d
одновременно не равны 0, ф-ии
(1)
где
числа a,
b,
c
и
d
одновременно не равны 0, ф-ии
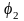 и
и разлагаются по степеням x
и
y,
начиная с не ниже второй степени, и
разлагаются по степеням x
и
y,
начиная с не ниже второй степени, и
 ,
сложное, т.е.
,
сложное, т.е.
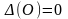 .
.
Случай
 .
.
Канонический
вид. Если
,
то с-ма
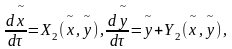 (2)
где
ф-ции
(2)
где
ф-ции
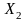 и
и
 разлагаются по степеням
разлагаются по степеням
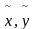 ,
начиная с не ниже второй степени, и
,
начиная с не ниже второй степени, и
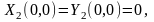 яв-тся каноническим видом с-мы (1).
яв-тся каноническим видом с-мы (1).
С-ма
(1) с помощью невырожденных линейных
однородных преобразований зависимых
переменных: 1)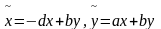 при
при
 ;
2)
;
2) при
при
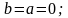 3)
3)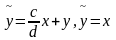 при
при
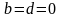 приводится к с-ме вида
приводится к с-ме вида
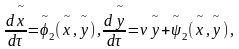 из
которой заменой
из
которой заменой
 получаем каноническую с-му (2).
получаем каноническую с-му (2).
Определение характера состояния равновесия.
1.Приводим
с-му (1) каноническому 3виду
 .
(3)
.
(3)
2.Подставляем
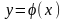 ,
где
,
где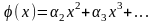 ,
в ур-ние
,
в ур-ние .
Методом неопределённых коэффициентов
находим
.
Методом неопределённых коэффициентов
находим
 (хотя
бы первые из них).
(хотя
бы первые из них).
3.Составляем
ф-цию
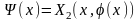 .
При этом достаточно найти первые
ненулевые коэффициенты в разложении
.
При этом достаточно найти первые
ненулевые коэффициенты в разложении
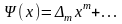 ,
где
,
где
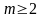 ,
а
,
а
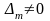 .
.
Узел.
Если
m
– нечётное, а
 ,
то СР О(0,0)
с-мы (3) (и системы (1)) будет узлом.
,
то СР О(0,0)
с-мы (3) (и системы (1)) будет узлом.
В
направлениях
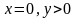 и
и
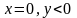 примыкает по одной О-кривой,
а каждом из направлений
примыкает по одной О-кривой,
а каждом из направлений
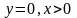 и
и
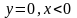 примыкает
пучок О-кривых
(рис.1) с-мы (3).
примыкает
пучок О-кривых
(рис.1) с-мы (3).
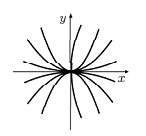 рис.1
рис.1
Седло.
Если
m
– нечётное, а
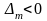 ,
СР О(0,0)
с-мы (3) (и с-мы (1) будеи седлом (рис.2)).
,
СР О(0,0)
с-мы (3) (и с-мы (1) будеи седлом (рис.2)).
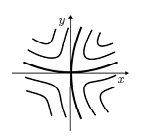 рис.2
рис.2
Сепаратрисы седла О(0,0) с-мы (3) примыкают в направлении координатных осей.
Седло-узел. Если m – чётное, то СР О(0,0) с-мы (3) (и с-мы (1)) яв-тся седло-узлом (рис.3).
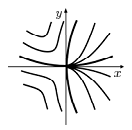 рис.3
Седло-узел
О(0,0)
с-мы (3) состоит из двух гиперболических
и одного параболического секторов
Бендиксона. В направлениях
и
примыкает по одной О-кривой
с-мы (3). В направлении
при
примыкает одна О-кривая
с-мы (3), а при
-
пучок
её О-кривых.
В напрвлении
при
примыкает пучок О-кривых
с-мы (3), а при
-
одна её О-кривая.
рис.3
Седло-узел
О(0,0)
с-мы (3) состоит из двух гиперболических
и одного параболического секторов
Бендиксона. В направлениях
и
примыкает по одной О-кривой
с-мы (3). В направлении
при
примыкает одна О-кривая
с-мы (3), а при
-
пучок
её О-кривых.
В напрвлении
при
примыкает пучок О-кривых
с-мы (3), а при
-
одна её О-кривая.
Случай
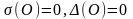 .
.
Канонический
вид. Если
,
то
с-ма
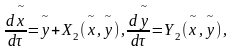 (4)
где
ф-ции
и
разлагаются по степеням
,
начиная с не ниже второй степени, и
яв-тся каноническим видом с-мы (1).
(4)
где
ф-ции
и
разлагаются по степеням
,
начиная с не ниже второй степени, и
яв-тся каноническим видом с-мы (1).
С-ма
(1) с помощью невырожденных линейных
однородных преобразований зависимых
переменных: 1)
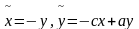 при
при
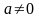 ;
2)
;
2)
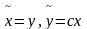 при
при
 приводится к системе вида
приводится к системе вида
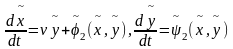 ,
из которой заменой
получаем каноническую с-му (4).
,
из которой заменой
получаем каноническую с-му (4).
Определение характера СР.
1.Приводим
с-му (1) каноническому виду
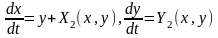 .
(5)
.
(5)
2.Подставляем
,
где
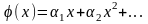 ,
в ур-ние
,
в ур-ние
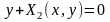 .
Методом неопределённых коэффициентов
находим
(хотя
бы первые из них).
.
Методом неопределённых коэффициентов
находим
(хотя
бы первые из них).
3.Составляем
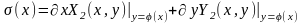 и
и
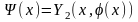 .
При этом в разложениях
.
При этом в разложениях
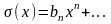 и
и
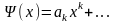 достаточно
найти первые ненулевые коэффициенты.
В случае
достаточно
найти первые ненулевые коэффициенты.
В случае
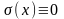 считаем
считаем
 .
.
Узел.
Если
k
–
нечётное (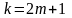 ),
а число n
– чётное, коэффициенты
),
а число n
– чётное, коэффициенты
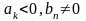 и выполняется одно из условий: а)
и выполняется одно из условий: а)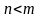 ;
б)
;
б)
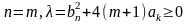 ,
то СР О(0,0)
с-мы (5) (и с-мы (1)) является узлом. Все
траектории этого сложного узла с-мы (5)
примыкают в направлении оси Ох
(рис.4).
,
то СР О(0,0)
с-мы (5) (и с-мы (1)) является узлом. Все
траектории этого сложного узла с-мы (5)
примыкают в направлении оси Ох
(рис.4).
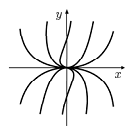 рис.4
рис.4
Седло.
Если
k
–
нечётное, а коэффициент
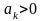 ,
то СР О(0,0)
с-мы (5) (системы (1)) яв-тся узлом. Сепоротрисы
седло О(0,0) Сис-мы (5) примыкает в направлении
оси Ох.
(рис.5).
,
то СР О(0,0)
с-мы (5) (системы (1)) яв-тся узлом. Сепоротрисы
седло О(0,0) Сис-мы (5) примыкает в направлении
оси Ох.
(рис.5).
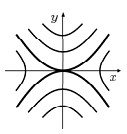 рис.5
рис.5
Это сложное седло иногда называют топологическим седлом.
Фокус
или центр. Если
k
–
нечётное (
),
а коэффициент
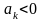 и выполняется одно из условий: а)
;
б)
и выполняется одно из условий: а)
;
б)
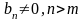 ;
в)
;
в)
 ,
,
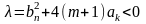 ,
то СР О(0,0)
с-мы (5) (и с-мы (1)) яв-ся фокусом или центром.
,
то СР О(0,0)
с-мы (5) (и с-мы (1)) яв-ся фокусом или центром.
Состояние равновесия с одним эллиптическим, двумя сопровождающими его параболическими и одним гиперболическим секторами Бендиксона.
Если k – нечётное ( ), а число n – нечётное, коэффициенты и выполняется одно из условий:
а) ; б) , то СР О(0,0) с-мы (5) (и с-мы (1))состоит из одного эллиптического, двух сопровождающих его параболических и одного гиперболического секторов Бендиксона.
Траектории с-мы (5) примыкают в направлении оси Ох.
Рис.6
выполнен для с-мы (5) при
 ,
а в случае
,
а в случае
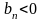 расположение траекторий получается
симметричным отображением относительно
оси Ох.
расположение траекторий получается
симметричным отображением относительно
оси Ох.
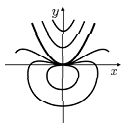 рис.6
рис.6
Вырожденное
состояние равновесия. Если
k
– чётное (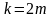 )
и выполняется одно из условий: а)
или б)
)
и выполняется одно из условий: а)
или б)
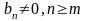 ,
то СР О(0,0)
с-мы (5) (и с-мы (1)) есть вырожденное
СР
(рис.7).
,
то СР О(0,0)
с-мы (5) (и с-мы (1)) есть вырожденное
СР
(рис.7).
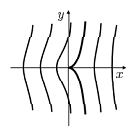 рис.7
рис.7
Вырожденное СР состоит из двух гиперболических секторов Бендиксона. Две сепаратрисы вырожденного СР О(0,0) системы (5) примыкают в направлении оси Ох. Иногда вырожденное СР наз-ют двухсепаратрисным селом.
Седло-узел.
Если
k
– чётное (
),
коэффициент
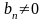 и
,
то СР О(0,0)
с-мы (5) (и с-мы (1)) яв-ся седлом-узлом
(рис.8).
и
,
то СР О(0,0)
с-мы (5) (и с-мы (1)) яв-ся седлом-узлом
(рис.8).
 рис.8
рис.8
У системы (5) все О-кривые седло-узла примыкают в направлении оси Ох: при в направлении примыкают две О-кривые, а в направлении примыкает пучок О-кривых (рис.8); при в направлении примыкает пучок О-кривых, а в направлении примыкают две О-кривые.
