
- •5. Частные производные 2-го порядка.
- •4. Теоремы о дифференцировании сложной функции 2ух переменных.
- •6. Экстремум функции 2ух переменных. Необходимое и достаточное условия экстремума функции нескольких переменных.
- •8.Свойства неопределённого интеграла
- •26. Понятие несобственных интегралов II рода. Пример интеграл Дирихле II рода.
- •27. Понятие дифференциального уравнения I порядка, его общего и частного решения
- •7.Понятие неопределенного интеграла. Таблица основных неопределенных интегралов.
- •9.Метод замены переменной, метод поднесения под знак дифференциала. Примеры.
- •10.Метод интегрирования по частям. Примеры.
- •31. Структура общего решения линейного однородного
- •32. Метод Эйлера (метод характеристического уравнения)
- •33. Структура общего решения линейного неоднородного
- •34. Метод вариации произвольной постоянной.
- •11.Двукратное интегрирование по частям на примере
- •12.Интегралы от функций, содержащих квадратный трехчлен . Примеры.
- •35. Понятие ряда. Классификация рядов. Примеры.
- •36. Сходящиеся и расходящиеся ряды. Исследование сходимости рядов вида
- •37.Необходимый признак сходимости ряда.
- •38. Признаки сравнения для знакоположительных рядов.
- •42.Признак Лейбница
- •41.Знакопеременные и знакочередующиеся ряды. Понятие абсолютной и условной сходимости. Знакочередующиеся ряды Лейбницевского типа
- •40.Интегральный признак Коши для знакоположительных рядов. Пример исследования сходимости обобщенного гармонического ряда
- •28. Ду с разделяющимися переменными. Пример
- •30. Линейные дифференциальные уравнения 1 порядка и уравнения Бернулли.
- •16 Интегрирование некоторых видов иррациональностей. Примеры.
- •18 Свойства определенного интеграла.
- •17.Понятие определенного интеграла, его геометрический и экономический смысл.
- •15.Интегрирование тригонометрических выражений. Универсальная тригонометрическая подстановка. Примеры.
- •20.Теорема о среднем.Её геометр. И эк.Интерпритац.
- •22.Формула Ньютона-Лейбница.
- •23.Замена перемен. В опред.И.Интегрир.По частям
- •1.Понятие фнп.Ее обл определения. Пределы фдп в точке. Непрерывность фдп в точке. Примеры
- •2.Частное приращение фдп. Частная производная фнп по одной из этих переменных. Примеры
- •3. Полное приращения фдп. Дифференциал фнп. Формула приближенных вычислений. Геометр смысл диф-ла.
- •21.Теорема об и с переменным верхним пределом
- •24.Вычисление площадей плоских фигур.
- •29. Геометрическая интерпретация общего решения и решения задачи Коши.
- •14.Интегрирование рациональных дробей с помощью разложения их на простейшие дроби. Примеры
40.Интегральный признак Коши для знакоположительных рядов. Пример исследования сходимости обобщенного гармонического ряда
Пусть
члены ряда
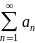 положительны
и убывают, т.е.
и пусть f(x)непрерывная,
положительная убывающая функция,
определённая для х>=1 и такая, что
f(1)=
,
f(2)=
положительны
и убывают, т.е.
и пусть f(x)непрерывная,
положительная убывающая функция,
определённая для х>=1 и такая, что
f(1)=
,
f(2)=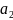 ,…,f(n)=
,…,f(n)=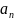 ,…,тогда
,…,тогда
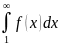 и ряд
сходятся или расходятся одновременно.
и ряд
сходятся или расходятся одновременно.
Исследуем
вопрос о сходимости ряда
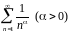 .
Решение. Применим интегральный признак
сходимости, тогда
.
Решение. Применим интегральный признак
сходимости, тогда
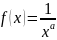 Эта функция удовлетворяет всем условиям
теоремы. Рассмотрим несобственный
интеграл
Эта функция удовлетворяет всем условиям
теоремы. Рассмотрим несобственный
интеграл
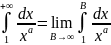
1.Если
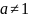 ,
то
,
то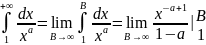 =
=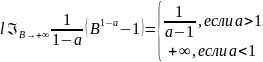
2.
Если
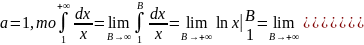 .
.
Ряд расходится. Тогда несобственный интеграл
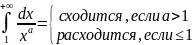
поэтому
и ряд, который является обобщенным
гармоническим
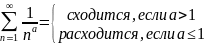
28. Ду с разделяющимися переменными. Пример
Уравнения вида y’ =f1(x)f2(y) называются уравнениями с разделяющимися переменными. Метод их решения состоит в нахождении множителя для преобразования в уравнение с разделенными переменными. Это : dx/f2(y), тогда уравнения запишутся так: dy/f2(y)=f1(x)dx. Проинтегрируем ∫dy/f2(y)=∫f1(x)dx. После получения общего решения необходимо проверить, являются ли нули функции f2(y) решениями заданного уравнения и заключены ли они в общем интеграле.
Пример 1
Решить
дифференциальное уравнение .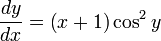
Разделим
переменные: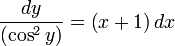
Т.
к. начальные условия не заданы, возьмем
неопределенный интеграл от обеих частей
уравнения:
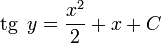
Осталось
лишь выразить у через х :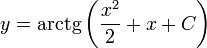
Найдем
также нулевые решения: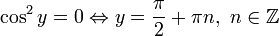
30. Линейные дифференциальные уравнения 1 порядка и уравнения Бернулли.
Уравнение вида y'+ρ(x)y=f(x), где ρ(x) и f(x) непрерывные функции, называется линейным дифференциальным уравнением первого порядка относительно у. Если f(x)=0, то уравнение называется линейным однородным, иначе- лин. Неоднород.
Лин. Однород.-это ур-е с раздел-ся переменными, его общее решение выражается формулой у=Се-∫p(x)dx. Для реш-я лин неоднород ур-я можно применить метод вариации произвольной постоянной, тогда общее реш-е неоднород
у=С(х) е-∫p(x)dx.
Уравнением Бернулли наз-ся ур-е вида y’+p(X)y=q(x)yα, где α-действительное число. В случае α=0,α=1 ур-е является линеным. Во всех других случаях оно сводится к линейному при помощи подстановки u=y1-α. Но можно решать подстановкой y=uv.Записав ур-е в виде u’v+(v’+p(x)v)u=q(x)uαvα, находим частное реш-е ур-я v’+p(x)v=0 и общее реш-е ур-я u’=q(x)uαvα-1.Тогда y(x)=u(x,C)v(x) даст общее реш-е ур-я Бернулли.
16 Интегрирование некоторых видов иррациональностей. Примеры.
Ин-л вида
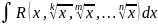 , где R
обозначена рац. ф-ция своих аргументов
сводиться к ин-лу от дробно-рац. ф-ции
с помощью замены переменной
, где R
обозначена рац. ф-ция своих аргументов
сводиться к ин-лу от дробно-рац. ф-ции
с помощью замены переменной
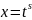 ;
;
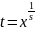 =
=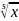 ,
где S
– наим. общ. кратное показателей всех
корней, входящих в подинтеграл. ф-цию
S=НОК(k,m,…n)
,
где S
– наим. общ. кратное показателей всех
корней, входящих в подинтеграл. ф-цию
S=НОК(k,m,…n)
Пр:
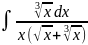 =
=
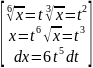 =
=
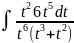 = 6
= 6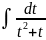 = 6
= 6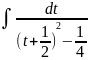 = 6
= 6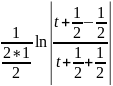 +
c=6
+
c=6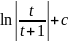 =6
=6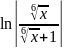 +C
+C
В и-лах вида
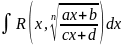 вводится подстановка t=
вводится подстановка t=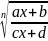 с помощью которой и-л рационализируется,
т. е. сводится к предыдущему методу.
с помощью которой и-л рационализируется,
т. е. сводится к предыдущему методу.И-лы, связанные с подстановкой Эйлера.
18 Свойства определенного интеграла.
Значение опред. и-ла – это число(любое).
Значение опред. и-ла не зависит от того, какой буквой обозначена переменная интегрирования, т. е.
 .
.
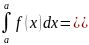 0.
В граф.иллюстрации этого случая (a=b)
отрезок ab
вырождается в точку, а криволин.трапеция
вырождается в отрезок, у которого
площадь=0
0.
В граф.иллюстрации этого случая (a=b)
отрезок ab
вырождается в точку, а криволин.трапеция
вырождается в отрезок, у которого
площадь=0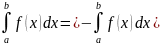
Св-во линейности опред.и-ла.
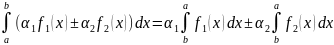
Св-во адитивности опред.и-ла.
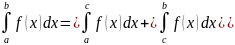 .
Это св-во справедливо для люб.взаимного
расположения точек a,b,c.
.
Это св-во справедливо для люб.взаимного
расположения точек a,b,c.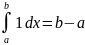
 Теорема
об интегрировании неравенств: если в
люб.точке x
отрезка ab
выполняется нер-во f(x)
Теорема
об интегрировании неравенств: если в
люб.точке x
отрезка ab
выполняется нер-во f(x)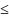 g(x),
то ф-ции f(x)
и g(x)
интегрируемы на отрезке ab
и выполняется нер-во:
g(x),
то ф-ции f(x)
и g(x)
интегрируемы на отрезке ab
и выполняется нер-во:
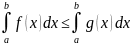
Теоремы об оценке опр.и-ла. 1)Если на отр. ab ф-ция удовлетворяет нер-ву m f(x) M, то опр. и-л от ф-ции удовл. нер-ву m(b-a)
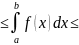 M(b-a).
2)Если ф-ция y=f(x)
интегрируема на отр. ab,
то
M(b-a).
2)Если ф-ция y=f(x)
интегрируема на отр. ab,
то
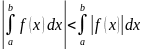
Теорема о среднем: если ф-ция y=f(x) непрерывна на отр. ab, то на этом отр. существует т.С, такая, что
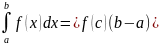 .
.
