
- •5. Частные производные 2-го порядка.
- •4. Теоремы о дифференцировании сложной функции 2ух переменных.
- •6. Экстремум функции 2ух переменных. Необходимое и достаточное условия экстремума функции нескольких переменных.
- •8.Свойства неопределённого интеграла
- •26. Понятие несобственных интегралов II рода. Пример интеграл Дирихле II рода.
- •27. Понятие дифференциального уравнения I порядка, его общего и частного решения
- •7.Понятие неопределенного интеграла. Таблица основных неопределенных интегралов.
- •9.Метод замены переменной, метод поднесения под знак дифференциала. Примеры.
- •10.Метод интегрирования по частям. Примеры.
- •31. Структура общего решения линейного однородного
- •32. Метод Эйлера (метод характеристического уравнения)
- •33. Структура общего решения линейного неоднородного
- •34. Метод вариации произвольной постоянной.
- •11.Двукратное интегрирование по частям на примере
- •12.Интегралы от функций, содержащих квадратный трехчлен . Примеры.
- •35. Понятие ряда. Классификация рядов. Примеры.
- •36. Сходящиеся и расходящиеся ряды. Исследование сходимости рядов вида
- •37.Необходимый признак сходимости ряда.
- •38. Признаки сравнения для знакоположительных рядов.
- •42.Признак Лейбница
- •41.Знакопеременные и знакочередующиеся ряды. Понятие абсолютной и условной сходимости. Знакочередующиеся ряды Лейбницевского типа
- •40.Интегральный признак Коши для знакоположительных рядов. Пример исследования сходимости обобщенного гармонического ряда
- •28. Ду с разделяющимися переменными. Пример
- •30. Линейные дифференциальные уравнения 1 порядка и уравнения Бернулли.
- •16 Интегрирование некоторых видов иррациональностей. Примеры.
- •18 Свойства определенного интеграла.
- •17.Понятие определенного интеграла, его геометрический и экономический смысл.
- •15.Интегрирование тригонометрических выражений. Универсальная тригонометрическая подстановка. Примеры.
- •20.Теорема о среднем.Её геометр. И эк.Интерпритац.
- •22.Формула Ньютона-Лейбница.
- •23.Замена перемен. В опред.И.Интегрир.По частям
- •1.Понятие фнп.Ее обл определения. Пределы фдп в точке. Непрерывность фдп в точке. Примеры
- •2.Частное приращение фдп. Частная производная фнп по одной из этих переменных. Примеры
- •3. Полное приращения фдп. Дифференциал фнп. Формула приближенных вычислений. Геометр смысл диф-ла.
- •21.Теорема об и с переменным верхним пределом
- •24.Вычисление площадей плоских фигур.
- •29. Геометрическая интерпретация общего решения и решения задачи Коши.
- •14.Интегрирование рациональных дробей с помощью разложения их на простейшие дроби. Примеры
37.Необходимый признак сходимости ряда.
Если
ряд
- сход., то предел общего члена при n→∞=0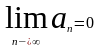
Док-во:рассмотрим n-ую частичную сумму ряда и (n-1)-ую частичную сумму ряда:
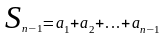
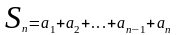
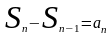
Возьмём предел обеих частей равенства:

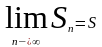
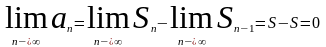
38. Признаки сравнения для знакоположительных рядов.
Теорема 1(признак сравнения):
Если
даны 2 ряда: 1)
,
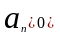 ; 2)
; 2)
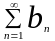 ,
,

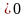 n=
1, 2,…
n=
1, 2,…
для
которых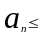 ,
то 1ый ряд наз-сяможарируемым, а 2ой –
можарантным.
,
то 1ый ряд наз-сяможарируемым, а 2ой –
можарантным.
Если 2ой ряд сход-ся, то сход-ся и 1й ряд. Если 1 ряд расх-ся, то расх-ся и 2ой ряд.
Теорема 2 ( признак сравнения в предельной форме):
Если даны 2 ряда: 1) , ; 2) , n= 1, 2,…
И , то
Если сущ-т предел
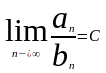 (С≠0, С≠∞), то оба ряда либо одновременно
сход-ся, либо одновременно расх-ся.
(С≠0, С≠∞), то оба ряда либо одновременно
сход-ся, либо одновременно расх-ся.Если
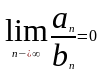 ,
то из сход-тиможарантного ряда следует
сход-тьможарируемого ряда.
,
то из сход-тиможарантного ряда следует
сход-тьможарируемого ряда.Если
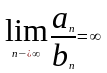 ,
то из расх-тиможарантного ряда следует
расх-тьможарируемого ряда.
,
то из расх-тиможарантного ряда следует
расх-тьможарируемого ряда.
Замечание: теорема 1 и 2 на практике не всегда удобны, т.к. для исследования сход-ти 1го из рядов необходимо знать поведение другого ряда или подбирать такой ряд, поведение которого известно.
Пример1:
исследовать
на сходимость ряд
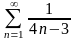
Сравним
его с гармоническим рядом
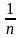 >
>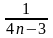
Гармонический ряд расх-ся, поэтому расх-ся и данный ряд по 1му признаку сравнения.
Пример2:
исследовать сход-ть ряда
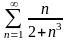 Для сравнения возьмём обобщенный
гармонический ряд
Для сравнения возьмём обобщенный
гармонический ряд
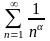 ,
кот-й сх-ся при α>1 и расх-ся при α≤1.
,
кот-й сх-ся при α>1 и расх-ся при α≤1.
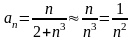 .
Ряд
.
Ряд
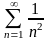 сх-ся.
Положим
сх-ся.
Положим
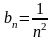 .
Применяем 2ой признак сравнения:
.
Применяем 2ой признак сравнения:
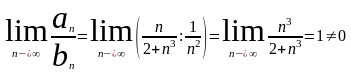
Мы сравнивали данный ряд со сх-ся рядом. По второму признаку сравнения данный ряд сх-ся.
39.Признак Даламбера и Коши для знакоположительных рядов. Примеры.
Признак
Даламбера:Для ряда
вычисляется предел отношения
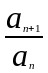 и сравнивается с 1.
и сравнивается с 1.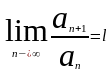
Если l> 1 , то исслед-ый ряд расх-ся
Если l< 1, то исслед-ый ряд сх-ся
Если l=1 , то о поведении ряда ничего сказать нельзя, нужны доп.исследования – другие признаки.
Пример:
исследовать на сход-ть ряд

 ,
,
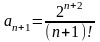
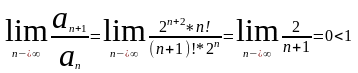 По
признаку Даламбера ряд сход-ся.
По
признаку Даламбера ряд сход-ся.
Признак Коши:
Для
ряда
вычисляется предел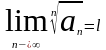 и сравниваем его с 1.
и сравниваем его с 1.
Если l> 1 , то исслед-ый ряд расх-ся
Если l< 1, то исслед-ый ряд сх-ся
Если l=1 , то о поведении ряда ничего сказать нельзя, нужны доп.исследования – другие признаки.
Пример:
исследовать на сход-ть ряд

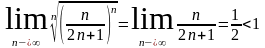 следовательно
ряд сх-ся.
следовательно
ряд сх-ся.
42.Признак Лейбница
Если
члены знакочередующегося ряда![]() убывают по абсолютной величине
убывают по абсолютной величине
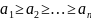 и
и
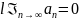 ,
то ряд сходится, а его сумма S
положительна и не превосходит первого
члена: S<=
,
то ряд сходится, а его сумма S
положительна и не превосходит первого
члена: S<=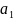
Пример![]() .
Ряд из модулей имеет вид
.
Ряд из модулей имеет вид![]() — это гармонический ряд, который
расходится.
— это гармонический ряд, который
расходится.
Теперь воспользуемся признаком Лейбница:
знакочередование
выполнено
![]() ,
,![]() ,
,![]()
Следовательно, так как все условия выполнены, но ряд из модулей расходится, искомый ряд сходится условнo
41.Знакопеременные и знакочередующиеся ряды. Понятие абсолютной и условной сходимости. Знакочередующиеся ряды Лейбницевского типа
Знакопеременный ряд – ряд, содержащий как положительные так и отрицательные члены. Знакопеременный ряд называется знакочередующимся, если его члены попеременно принимают значения противоположных знаков .
Если
ряд, состоящий из абсолютных величин,
сходится, то знакочередующийся ряд
сходится абсолютно.
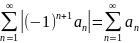 .
В случае, если ряд
сходится при отсутствии абсолютной
сходимости, то он называется условно
сходящимся.
.
В случае, если ряд
сходится при отсутствии абсолютной
сходимости, то он называется условно
сходящимся.
Знакочер-ся ряды называются рядами л.типа, если они удовлетворены двум условиям:
1)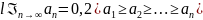 .
.
Примеры:

