5. Частные производные 2-го порядка.

Пусть в некоторой окрестности точки (x₀ ,y₀) задана функция f(x,y). Фиксируя переменную y(y=y₀), получим функцию одной переменной x: f(x,y₀). Обычная производная этой функции в точке x=x₀ называется частной производной функции f(x,y) в точке (x₀,y₀) по x и обозначается

Т.о,

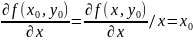
Если вспомнить определение производной функции одной переменной, то

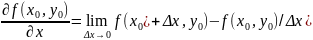
Или, если ввести обозначение

f(x₀ + Δx, y₀) – f(x₀, y₀) = Δ_xf

Где Δ_xf – приращение функции по переменной x, то

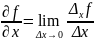
Аналогично вводится частная производная по y:

Или

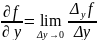
Где Δ_yf – приращение функции по y.

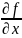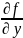и - единые символы, так как в них числитель и знаменатель не имеют самостоятельного смысла. По аналогии с функциями 1ой переменной линейные функци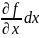и и , переменных dx и dy, называемых дифференциалами независимых переменных, называются частными дифференциалами функции f(x,y) соответственно по переменным x и y обозначаются так:

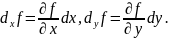
Аналогичные определения имеют место для любого числа переменных.

Для нахождения частной производной функции 2ух переменных по переменной x(y) необходимо применять правило дифференцирования и таблицу производных для функции 1ой переменной считая всё что x(не y) константой.

4. Теоремы о дифференцировании сложной функции 2ух переменных.

Теорема1.

Если Ƶ=f(x,y) и x=x(t), y=y(t), то производная

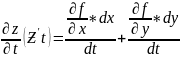
Если в функцию Ƶ подставить вместо х и у соответствующие функции, зависящие от переменной t, то в результате получим Ƶ(t), дифференцируя которую по t, и получим ответ Ƶ’t=Ƶ’= ;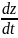

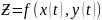
Теорема 2.

Если функция Ƶ – функция 2ух переменных, которые в свою очередь являются также функциями 2ух переменных, то для функции Ƶ можно найти 2е частные производные по u и v.

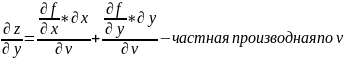
Если до дифференцирования в исходную функцию Ƶ вместо x и y подставить зависимость от u и v

, то в результате получим функцию 2ух переменных u и v =Ƶ (u,v), поэтому необходимо найти 2е производные.

Производные высших порядков.

Для 2ух переменных: Ƶ = f(x,y) :

1. Ƶ ‘_x = 2) Ƶ ‘_y =

1. Ƶ “_xx = 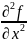1.2) Ƶ “_xy = 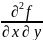2.1) Ƶ “_yx = 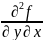2.2) Ƶ “_yy =

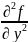
1.2 и 2.1 – вторые смешанные производные функции2ух переменных.

Теорема: при условии существования непр-ти частных смешанных производных справедливо равенство 1.2 и 2.2, т.е порядок дифференцирования не влияет на результат. Эту теорему можно обобщить и на производные более высокого порядка:

6. Экстремум функции 2ух переменных. Необходимое и достаточное условия экстремума функции нескольких переменных.

Т

Ɛ M₀

очка М₀ называется точкой локального минимума для функции Ƶ = f(x, y), если для любой точки М є Ɛ окрестности точки М₀ справедливо неравенство:

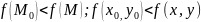
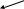В окрестности множество точек, лежащие внутри

Круга с центром в точке М₀ и радиусом Ɛ. (Ɛ→0)

Аналогично определяется и локальный максимум: точка М₀ – точка локального максимума для функции Ƶ = f(x, y), если для любой точки М из Ɛ окрестности точке М справедливо неравенство:

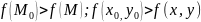
На практике для нахождения экстремумов необходимы 2 условия в виде теорем:

Теорема 1. (необходимое условие существования экстремума в точке М₀)

Если М₀ – точка локального экстремума, то в точке М₀ 1ые производные функции 2ух переменных обращаются в 0.

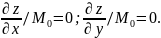
Несмотря на то, что это условие является необходимым, оно используется для выбора среди точек из области определения ряда точек, в которых может быть экстремум. Конкретно для выбора экстремальных точек среди уже отобранных с помощью Теоремы 1 , применяется Теорема 2(критерий Сильвестра).

Теорема 2. Функция Ƶ = f(x, y) имеет в М₀ экстремум, если определитель 2го порядка, состоящий из всевозможных 2ых производных функции 2ух переменных и вычисленный в этой точке М₀ 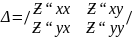>0. >0

⃒M₀=(x₀, y₀)

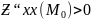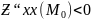Характер экстремума определяется по 1му элементу, а именно, если , то в точке М₀ достигается минимум, если , то в точке М₀- максимум.

Если при вычислении Δ он окажется < 0 , то в точке М₀ экстремума нет, если Δ = 0, то вопрос о существовании экстремума в точке M₀ остается открытым – нужны дополнительные исследования.

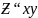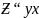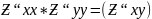Ввиду того, что = ( при выполнении условия теоремы) критерий можно переписать в следующем виде: Δ = ²⃒М₀