8.Свойства неопределённого интеграла

1. (òf(х)dх)'= f(х)

(òf(х)dх)'=(F(x)+C)'=F'(x)+C'= f(х)

2.Интеграл от дифференциала ф-ции f(х) равен самой ф-ции f(х) òd f(х)= f(х)

3.Свойство линейности. Интеграл от линейной комбинации двух ф-ций равен

ò( α₁f₁(х)± α₂f₂(х))dх= α₁ òf₁(х)dх± α₂òf₂(х)dх

Св-во 1 неопред. интеграла будем использовать на практике для проверки правильности нахождения неопред. интеграла.

В рез-те дифференцирования любой ф-ции, заданной в виде линейной комбинации элементарной ф-ции всегда получается также комбинация элементарной ф-ции. При нахождении неопред. интеграла от комбинации элементарных ф-ций не всегда получается комбинация элементарн. ф-ций, т.е. не все комбинации элементарн. ф-ций интегрируются, т.е. интегралы не от всяких ф-ций берутся.

Известные примеры «не берущихся» интегралов

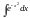- интеграл Пуасона

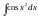- интеграл Кринеля

25. Понятие несобственных интегралов I рода. Пример интеграл Дирихле I рода.

Если в определении определенного интеграла нарушено либо условие непрерывности функции, либо условие конечности отрезка интегрирования, то имеем дело с НИ.

1. Если отрезок интегрирования [a,b]- бесконечен, то НИ-1

2. Если подынтегральная функция y=f(x) разрывна на отрезке [a,b], то НИ-2

Рассмотрим НИ-1. Их может быть 3 варианта: 1) 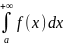2) 3)

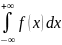
Дадим определение НИ-1первого варианта: =

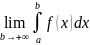
В случае если при вычислении НИ-1 получается константа, то говорят, что НИ-1 сходятся к этому числу. В случае если в ответе получается ∞ или предел не существует, то говорят, что НИ-1 расходится.

Аналогично определения и других НИ-1: ;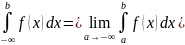

Пример: = = =

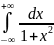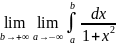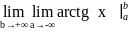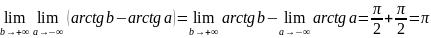
Вывод: НИ сходится к π.

26. Понятие несобственных интегралов II рода. Пример интеграл Дирихле II рода.

Рассмотрим НИ-II. Они возникают, если пытаться на конечном отрезке интегрирования [a,b] интегрировать разрывную подынтегральную функцию.

Пример: 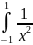dx =

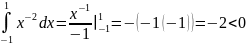
Интеграл вычислен с ошибкой. Подынтегральная функция y=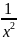 в точке 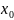= 0 имеет разрыв 2 рода, =0 принадлежит [-1,1]. Т.е. подынтегральная функция является разрывной на отрезке интегрирования [-1,1], следовательно, нарушается условие теоремы Ньютона-Лейбница, поэтому решение не верно. Для того, чтобы решить НИ-II необходимо знать как он определяется.

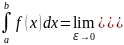
Возможны 2 случая:

1. НИ-II расходится

2. НИ-II сходится к какому-то члену

Пример:

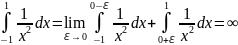
y=f(x), x принадлежит [-1,1]

Найдём отдельно =

=

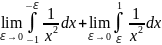
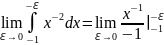Аналогично 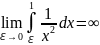. Т.к. оба предела равны ∞, то НИ : 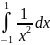расходится.

27. Понятие дифференциального уравнения I порядка, его общего и частного решения

ДУ – это связь между независимой переменной х, зависимой переменной у и её производными различных порядков. F(x, y,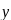 , …, 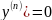(1)

Порядком ДУ называется наивысший порядок входящей в него производной. Для того, чтоб уравнение было дифференциальным необходимо, чтоб в него входила какая-либо производная Y, иначе это не будет ДУ.

Решением ДУ является всякая функция y=f(x), которая будучи подставленной в уравнение (1) обращает его в тождество. Основным методом нахождения решения ДУ является интегрирование. Т.к. в процессе интегрирования (нахождения неопределённого интеграла) находится семейство первообразных, то общее решение ДУ (1) содержит произвольные постоянные. Кол-во произвольных постоянных в общем решении ДУ (1) зависит от максимального порядка производных, т.е. если ДУ-II, то в общем решении будет содержаться 2 произвольных постоянных С1 и С2. Если ДУ-III – три произвольных постоянных (С1, С2 и С3) и т.д. Далее подробно будем изучать ДУ-I.

ДУ-1

F(x, y, ) = 0

yобщ=ϕ(х,с) – общее решение

y= ϕ(х,с) называется общим решением ДУ-1, если она удовлетворяет устоловиям:

1. прилюбых значениях С функция y= ϕ(х,с) является решением уравнения первого порядка.

2. для любых начальных условий (х0;у0) принадлежит D существует такое значение постоянной С, что выполняется равенство у0= ϕ(х0,С)

Если в общем решении ДУ-1 зафиксировать произвольную С, то получим так называемое частное решение. Т.о. общее решение ДУ состоит из совокупности всевозможных частных решений.