11.Двукратное интегрирование по частям на примере

В интегралах вида 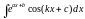применяется двукратное интегрирование по частям, где u и dv могут быть выбраны произвольным образом, но при повторном интегрировании, также как при первом.

Точно также .

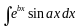Пример:

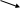
А

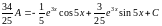
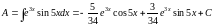
Двукратное интегрирование по частям в данном интеграле с постоянным выбором u и v привёл нас в итоге к исходному интегралу, перенося кот. из прав. части в левую и приводя подобные, находим ответ.

12.Интегралы от функций, содержащих квадратный трехчлен . Примеры.

Интегралы вида 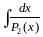, берутся с помощью замены переменной, предварительно выделив в многочлене полный квадрат.

Пр:

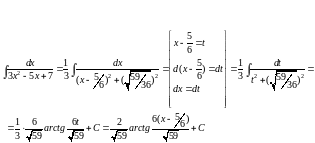
Для нахождения интеграла типа необходимо выполнить следующий алгоритм:

1)находим производную квадратного трёхчлена, стоящего в знаменателе, т.е.

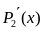
2)формируем эту производную в числителе под интегральной ф-цией

3)разбиваем полученный интеграл на 2 вида

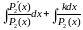
Второй интеграл типа 1, а первый интеграл берётся поднесением 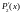под знак дифф-ла

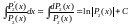
Пр:

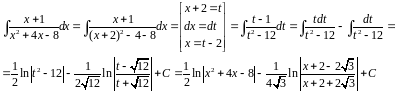
35. Понятие ряда. Классификация рядов. Примеры.

Ряд- a₁+a₂+…+a_n+… (1), где в зависимости от стр-ры общего члена ряда an ф-ла (1) может описывать как числовой ряд, если a_n задается числовой формулой или (1) – функциональный ряд, если a_n задается функцией.

Классификация рядов:

1. числовые и функциональные:

• числовые: a₁+a₂+…+a_n+…

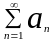
• функциональные:

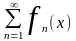
2. расходящиеся и сходящиеся

3. Числовые ряды делятся на знакопостоянные и знакопеременные (знакочередующиеся)

Также приведем некоторые примеры числовых рядов, имеющих важное практическое значение:

1. 0+0+…+0+…= 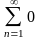= 0 – ряд сходится

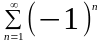2. = -1+1-1+1-1… - знакочередующийся

S_n=

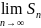
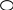
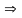= ряд расходится

3. 1 + ½ + 1/3 + 1/4 + … +1/n+… = - гармонический ряд, расходящийся

4. Примером ряда может служить сумма бесконечная геометрическая прогрессия виды:

a+ a*q+a*q²+…+a*q^n-1+… = 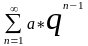, a≠0

36. Сходящиеся и расходящиеся ряды. Исследование сходимости рядов вида

Ряды бывают: сходящиеся и расходящиеся.

Если в ряде a₁+a₂+…+a_n+… (1) взять сумму первых n-слагаемых, то получим n-ую частичную сумму ряда (S_n)

S_n=a₁+a₂+…a_n(2)

Ряд (1) называется сходящимся, если сущ-ет конечный предел при n→∞, n-ой частичной суммы ряда, т.е.: =S (*), т.к. предел существует и конечен, то он = константе S.

Теорема: для сходящегося ряда справедлива формула S=S_n+R_n, где R_n– n-ый остаток ряда, предел которого при n→∞равен 0.

Доказательство: рассмотрим ф-лу (1) в развернутом виде:

a ₁+a₂+…+a_n+a_n+1+a_n+2+…=S_n+R_n

S_n R_n

Возьмем предел от суммы:

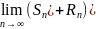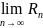= + = = S

Т.к. ряд сходится, то справедлива ф-ла (*),значит = S.

S=S_n+R_n(3)

Т.к. S- константа, то по т. о пределе константы:

В ф-ле (3) S - называется суммой ряда

Sn – энная частичная сумма ряда

Rn – энный остаток ряда

Примером ряда может служить сумма бесконечная геометрическая прогрессия вида:a+ aq+aq²+…+aq^n-1+… = , a≠0

Вычислим для данного ряда S, для этого рассмотрим S_n:

S_n = a+aq+aq²+…+aq^n-1 =

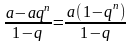
Для того что бы найти S и сделать вывод о сходимости или расходимости ряда вычислим предел S_nпри n→∞:

=

Вычисление предела зависит от того, какое значение принимает q.

Рассмотрим три случая:

1. │q│>1, ∞

2. │q│<1,

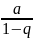
3. │q│=1, при q=-1,предел не существует

При q=1, = = ∞

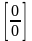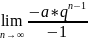Вывод:беск. сумма прогр. сходится к числу , при │q│<1; беск. сумма прогр. расходится в случае │q│≥1.

Далее рассмотри гармонический ряд 1 + ½ + 1/3 + 1/4 + … +1/n+…

a_n = 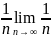=0

Еслиlim общ.члена ряда при n→∞равен 0, то о сходимости ряда ничего неизвестно, т.е. нужны дополнительные исследования.