7.Понятие неопределенного интеграла. Таблица основных неопределенных интегралов.
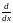
y
=f(x)
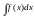
С
помощью неопред. интеграла находится
любая первообразная y=f(x),
кот. будем обознач. F(x).
Первообразная для ф-ции y=f(x)
наз. функция w=
F(x)
такая, что производная
.
По определению неопред. интеграла
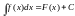(1) По определению (1) константа С
определяет
любую первообразную.
Пример: y=f(x)=cosx
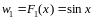
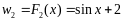
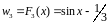
Фактически правая часть ф-лы(1) определяет семейство первообразных. Таким образом для нахождения неопред. Интеграла какой-либо ф-ции необходимо найти её любую первообразную и в ответ записать сумму найденных первообразных константы С.
Таблица основных неопределенных интегралов.
1.ò0dх=С.
2.
òхadх=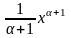
+С,
a¹-1.
3.
ò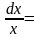
ln|х|+С,
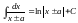
4.
,
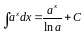следствие
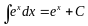
5.
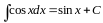
6.
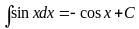
7.
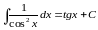
8.
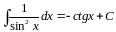
9.
10.
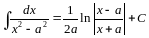
11.
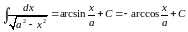
12.
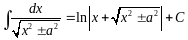
9.Метод замены переменной, метод поднесения под знак дифференциала. Примеры.
Если
y=f(x)
зависит от дифференцируемой ф-ции
x=φ(t),
то неопред. интеграл
.
Доказательство этой ф-лы опирается на
теорему сложной ф-ции.
Пр:
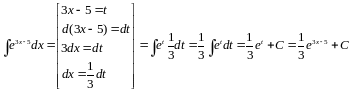
Св-ва
дифф-ла:
,
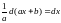применяя эту ф-лу удобнее использовать
метод внесения под знак дифф-ла, а уже
затем замену переменной.
Пр:
.
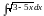Сформируем под знаком дифф-ла выражение,
стоящее под корнем.
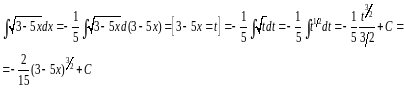
10.Метод интегрирования по частям. Примеры.
Теорема: если ф-ции u и v дифференцируемы, а также дифференцируемо их произведение, то интеграл от udv равен
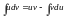
Док-во: найдем дифф-л произведения ф-ции uv
d(uv)=udv+vdu
udv=d(uv)-vdu интегрируем обе части равенства
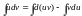
(1)
Суть
этой ф-лы состоит в том, что при правильном
выборе ф-ции u
и
v,
стоящий в правой части интеграл форм.
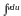должен оказаться проще, чем исходный
интеграл в левой части
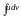
Пр:
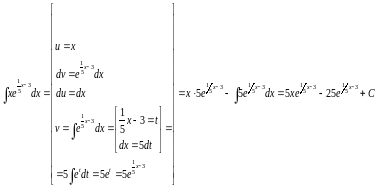
При восстановлении ф-ции v с помощью интегрирования в ф-ле интегрирования по частям константу С полагают равную 0 или не пишут.
При применении ф-лы(1) для того, чтобы интеграл vdu стал проще исходного интеграла, необходимо правильно выбирать в исходном интеграле ф-ции u и dv.
Общая рекомендация по выбору ф-ции u: ф-ция u должна быть выбрана с учётом того, что её производная или дифф-л должны бытьпроще самой ф-ции. Общая рекомендация распадается на более конкретные рекомендации.
В
интегралах вида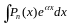
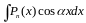
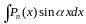
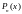-многочлен
степени n
от переменной
x
В
этих 0интегралах в качестве u
выбирают
,
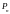всё остальное dv.
Если -многочлен степени выше первой, то ф-лу интегрирования по частям нужно применять неоднократно!
В интегралах вида
,
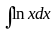
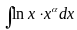в качестве u
выбирается
lnx,
всё остальное dv.
В интегралах вида
,
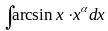
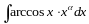
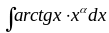
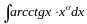в качестве u
выбирают обратные тригонометрич.
выраж., всё остальное.
31. Структура общего решения линейного однородного
дифференциального уравнения II порядка.
y’’ + py’ + qy =f(x) (1)
если f(x)=0, то уравнение называется однородным.
В случае если у однородного уравнения p(x) и q(x)- const.
То уравнение примет вид y’’ + py’ + qy = 0 , которое называется ЛОДУ II
порядка с постоянными коэффициентами. y’’ + py’ + qy = 0 (2)
Ур-е (2) имеет общее решение, которое может быть представлено в
виде, где у1 и у2 линейно независимые решения ур-я (2). (ф-ии y1 и y2 назыв. линейно-
независимыми на [a;b] если y1(x)/ y2(x) не явл. const
при х принадлежащем [a;b])
yоо=С1у1+С2у2 (3)
yоо – общее решение однородного ур-я.
Док-во. для того чтобы док-ть что уоо явл решением ДУ (2), то по определению
ДУ (3) будучи подставленным в ДУ (2) оно должно обращать его в равенство,
иначе (3) не является решением (2).
Подставляем (3) в (2), для этого предварительно найдем 1-ую и 2-ую производную.
y'оо= c1y’1+c2y’2
y'’оо= c1y’’1+c2y’’2
имеем
(c1y’’1+c2y’’2)+p(c1y’1+c2y’2)+q(С1у1+С2у2)=0
Раскроем скобки и перегруппируем слагаемые.
С1( y1’’+py1’+qy1)+ С2(y2’’+py2’+qy2)=0
Каждая из этих скобок тождества равны 0, т.к по условию теоремы
у1 и у2 – решения ур-я (2)
Т.О нами доказано что уоо будучи подставленным в (2) вместо у,
обратил его левую часть в 0, а это значит, что уоо,
описанный формулой (3) является решением уравнения(2).
yoo=eαx(C1cosβx + C2sinβx)