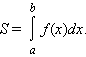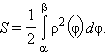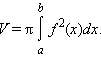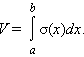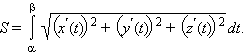- •Определители и их св-ва.
- •Миноры и алгебраические дополнения
- •Методы вычисления определителей
- •Обратная матрица. Теорема о существ обратной матрицы.
- •Элементарные преобразования матрицы.
- •Ранг матрицы. Правило вычисления ранга матрицы.
- •Системы n линейных алгебраических уравнений с n неизвестными
- •Правило Крамера
- •Теорема Кронекера-Капелли.
- •Метод Гаусса.
- •Вектора. Коорд вектора в декартовой системе координат.
- •Направляющие косинусы вектора
- •Скалярное произведение векторов. Его свойства.
- •.Векторное произведение векторов. Его св-ва.
- •Смешанное произведения векторов
- •Общее уравнение плоскости
- •Уравн плоскости проходящей через три точки в отрезках
- •Параметрическое и каноническое уравнение прямой
- •Уравнение прямой, проходящей через 2 точки
- •Уравнением прямой с угловым коэффициентом k.
- •Угол между прямыми на плоскости.
- •Эллипс. Каноническое уравнение.
- •Каноническое уравнение гиперболы
- •Парабола. Каноническое уравнение.
- •Функция. Характеристики поведения. Сложная функция.
- •Пределы функций, их свойства.
- •Теоремы о пределах.
- •Первый замечательный предел.
- •Второй замечательный предел( показательно-степенной предел)
- •Непрерывность функции в точке. Свойства непрерывных функций.
- •Точки разрыва функции. Их классификации.
- •Производная функции, ее геометрический смысл.
- •Основные правила дифференцирования
- •Дифференцирование тригонометрических и обратных им функций.
- •Дифференцирование логарифмических, показательных и степенных функций
- •Логарифмическое дифференцирование
- •Дифференцирование обратных функций и функций заданных параметрически
- •Дифференциал функции. Геометрический смысл дифференциала.
- •Формула Тейлора.
- •Возрастание и убывание функций. Точки экстремума.
- •Необходимое условие существования экстремума.
- •Критические точки. Достаточные условия существования экстремума.
- •Исследование функции на экстремум с помощью производных высших порядков.
- •Выпуклость и вогнутость кривой. Точки перегиба.
- •Асимптоты.
- •Функции нескольких переменных (Определение, примеры).
- •Пределы функции нескольких переменных и их свойства
- •Частное и полное приращение функций нескольких переменных.
- •Непрерывность функции нескольких переменных их св-ва
- •Частные производные первого и высших порядков
- •Теорема о смешанных производных второго порядка
- •Полный дифференциал.
- •Касательная плоскость и нормаль к поверхности.
- •Формула Тейлора для функций нескольких переменных
- •Экстремум функции нескольких переменных.
- •Необходимые и достаточные условия существования безусловного экстремума.
- •Максимум и минимум функции нескольких переменных.
- •Первообразная.
- •Неопределенный интеграл и его свойства
- •Замена переменных в неопределенном интеграле
- •Простейшие приемы интегрирования. Интегрирование по частям.
- •Простейшие приемы интегрирования. Интегрирование способом замены переменной.
- •Разложение рациональных дробей на простейшие.
- •Интегрирование элементарных дробей.
- •Интегрирование рациональных функций
- •Интегрирование иррациональных функций.
- •Интегрирование тригонометрических функций
- •Задачи, приводящие к понятию определенного интеграла
- •Верхние и нижние интегральные суммы
- •Определенный интеграл, его свойства и простейшие методы интегрирования
- •Основные свойства определенного интеграла.
- •Геометрический и физический смысл определенного интеграла.
- •Формула Ньютона-Лейбница.
- •Приложения определенного интеграла к решению геометрических и механических задач.
- •1. Площадь плоской фигуры.
- •2. Площадь криволинейного сектора.
- •3. Объем тела вращения.
- •4. Длина дуги кривой.
- •5. Площадь поверхности вращения.
- •Вычисление работы сил
- •Несобственные интегралы первого рода
- •Несобственные интегралы второго рода
- •Длина дуги кривой.
- •Вычисление площадей в прямоугольных координатах.
- •Вычисление объема тела.
- •Объем тела вращения
- •Двойной интеграл.
- •Вычисление двойного интеграла
- •Классификация точек разрыва функции
- •Числовой ряд, сумма ряда.
- •Необходимое условие сходимости ряда.
- •Доказательство
- •Признаки сравнения. Признак Даламбера.
- •Признаки сравнения. Признак Коши.
- •Интегральный признак Коши
- •Интегральный сходимости знакопостоянных рядов.
- •Знакочередующийся ряд. Теорема Лейбница.
- •Степенной ряд. Теорема Абеля.
- •Интервал и радиус сходимости степенного ряда.
- •Дифференциальные уравнения первого порядка. Общее и частное решения.
- •Уравнения с разделенными и разделяющимися переменными.
- •Однородные уравнения первого порядка.
- •. Линейные однородные дифференциальные уравнения. Решение уравнения.
- •Уравнения в полных дифференциалах.
Основные свойства определенного интеграла.
I. Величина определенного интеграла не зависит от обозначения переменной интегрирования, т.е., где х, t – любые буквы.
![]()
II. Определенный интеграл с одинаковыми пределами интегрирования равен нулю.
![]()
III. При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный.
IV. Если промежуток интегрирования [a,b] разбит на конечное число частичных промежутков, то определенный интеграл, взятый по промежутке [a,b], равен сумме определенных интегралов, взятых по всем его частичным промежуткам.
![]()
V. Постоянный множитель можно выносить за знак определенного интеграла.
VI. Определенной интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций.
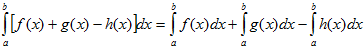
Геометрический и физический смысл определенного интеграла.
Геометрический.
Определённый интеграл
![]() численно равен площади фигуры,
ограниченной осью абсцисс, прямыми
численно равен площади фигуры,
ограниченной осью абсцисс, прямыми
![]() и
и
![]() и графиком функции
и графиком функции
![]() .
.
Физический. Путь S, пройденный телом при прямолинейном движении со скоростью v(t) за интервал времени от t1 до t2, вычисляется по формуле
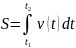
Формула Ньютона-Лейбница.
Формула Ньютона — Лейбница или основная теорема анализа даёт соотношение между двумя операциями: взятием определенного интеграла и вычислением первообразной.
Пусть функция f (x) непрерывна на [a; b], а F (x) – какая-либо первообразная функции f на этом отрезке. Тогда
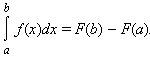
|
Таким образом, для вычисления определенного интеграла нужно найти какую-либо первообразную F функции f, вычислить ее значения в точках a и b и найти разностьF (b) – F (a).
Приложения определенного интеграла к решению геометрических и механических задач.
Геометрические приложения:
1. Площадь плоской фигуры.
Площадь криволинейной трапеции, ограниченной неотрицательной функцией f (x), осью абсцисс и прямыми x = a, x = b, определяется как
|
2. Площадь криволинейного сектора.
Рассмотрим кривую ρ = ρ (φ) в полярной системе координат, где ρ (φ) – непрерывная и неотрицательная на [α; β] функция. Фигура, ограниченная кривой ρ (φ) и лучами φ = α, φ = β, называется криволинейным сектором. Площадь криволинейного сектора равна
|
3. Объем тела вращения.
Пусть тело образовано вращением вокруг оси OX криволинейной трапеции, ограниченной непрерывной на отрезке [a; b] функцией f (x). Его объем выражается формулой
|
Пусть тело заключено между плоскостями x = a и x = b, а площадь его сечения плоскостью, проходящей через точку x, – непрерывная на отрезке [a; b] функция σ (x). Тогда его объем равен
|
4. Длина дуги кривой.
Пусть задана кривая
![]() .
Тогда длина ее участка, ограниченного
значениями t = α и t = β выражается
формулой
.
Тогда длина ее участка, ограниченного
значениями t = α и t = β выражается
формулой
|
|