58. Первообразная.

1.Первообразная. Функция F(х) называется первообразной для функции f (х) на промежутке X, если для любого х из Х выполняется равенство F'(x)=f(x)

   2. (Если F(х)-первообразная для функции f(х) на промежутке X, то у функции f(x) бесконечно много первообразных, и все эти первообразные имеют вид F (x)+С, где С - произвольная постоянная (основное свойство первообразной).

3.Правила вычисления первообразных:          1. Если F(х)-первообразная для f(x), а Н(х)-первообразная для h(х), то F(х)+Н(х)- первообразная для f(х)+h(х). Иными словами, первообразная суммы равна сумме первообразных.          2. Если F(х) - первообразная для f(х) и k - постоянная, то kF(х) - первообразная для kf(х). Иными словами, постоянный множитель можно вынести за знак первообразной.          3. Если F(х) - первообразная для f(х) и k, b- постоянные, причем k≠0, то F(kx+b) - первообразная для f (kх+b).

59. Неопределенный интеграл и его свойства

     Первообразной функции f на промежутке I называется функция F, такая, что

     Неопределенный интеграл

где F - первообразная функции f (на промежутке); C - произвольная постоянная.

**************************************************************************

Функция F(x) называется первообразной функции f(x), если

Множество всех первообразных некоторой функции f(x) называется неопределенным интегралом функции f(x) и обозначается как

Таким образом, если F - некоторая частная первообразная, то справедливо выражение

где С - произвольная постоянная.

     Основные свойства:

4. 

5. Замена переменных в неопределенном интеграле

     1.

     2. Если - первообразная для то

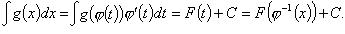
60. Простейшие приемы интегрирования. Интегрирование по частям.

Теорема. Пусть функции u и υ определены и дифференцируемы на некотором промежутке Т и функция du·υимеет на этом промежутке первообразную. Тогда функция u·dυ также имеет первообразную на промежутке Т, причем справедлива формула

òudυ = uυ - òυdu.

Доказательство. Найдем дифференциал от их произведения  u · υ. d(uυ) = du·υ + u·dυ.

Проинтегрируем обе части этого равенства. òd(uυ) = ò(du·υ + u·d υ). uυ = ò υdu + ò udυ,

ò udυ = uυ - ò υdu  -  формула интегрирования по частям.

С помощью этой формулы первообразная частично находится, и оставшиеся интегральные слагаемые, как правило, - проще исходного интеграла.

,где W(х) - некоторый многочлен, а второе слагаемое представляет собой правильную дробь, у которой степень числителя меньше степени знаменателя. Например, рассмотрим неправильную дробь

61. Простейшие приемы интегрирования. Интегрирование способом замены переменной.

Пусть требуется найти интеграл 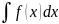, причём первообразную для 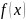мы подобрать не можем. Значит воспользуемся заменой. Метод интегрирования подстановкой (замены переменной) заключается во введении новой переменной интегрирования (то есть подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся.

Сделаем подстановку   где   — функция, имеющая непрерывную производную.

Тогда   и получаем формулу интегрирования подстановкой: