1. Определители и их св-ва.

Определитель (детерминант) — одно из основных понятий линейной алгебры. Это алгебраическая сумма произведений элементов матрицы, взятых по одному из каждой строки и каждого столбца. Определитель матрицы А обозначается как: det(A), |А| или Δ(A).

Det A=Σ(-1)^s(L)a_1L1+a_2L2…a_nLn S(L) – минимальное число перестановок, которые нужно сделать, чтобы перейти от основной установки чисел к перестановке L=(L₁ L₂… L_n). Основная перестановка – (1 2 3…n). Перестановка местами любых двух элементов называется транспозицией. Каждая транспозиция меняет знак определителя.

Свойства определителей:

1. Det A=Det A^T

2. Если хотя бы одна строка (столбец) матрицы нулевая, то определитель равен нулю. (ноль входит в каждое слагаемое)

3. Общий множитель элементов какого-либо ряда det можно вынести за знак det.

4. Если в det поменять местами 2 параллельных столбца или строки, то знак определителя изменится на противоположный.(будет отличаться только одной перестановкой)

5. Сумма произведений всех эл-в любой строки на их алг дополнения = det.

6. Если две строки (столбца) матрицы совпадают, то её определитель равен нулю(знак не меняется на противоположный, такое возможно только если будет 0) .

7. Сумма произведений всех элементов любого ряда на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю.(эта сумма соответствует определителю, у которого 2 одинаковые строки)

8. Сумма произведений всех элементов любого ряда на алгебраические дополнения равна величине определителя.

9. Если эл-ты некоторого столбца(строки) det равны сумме 2-х или больше числа слагаемых, то det равен сумме 2-х или более определителей того же порядка.(разложим определитель по элементам первого столбца)

10. При добавлении к любой строке (столбцу) линейной комбинации других строк (столбцов) определитель не изменится.

11. det произведения квадратных матриц одинакового порядка равен произведению их определителей (cм. также формулу Бине-Коши). Det(A,B)=detA *debt

2. Миноры и алгебраические дополнения

Минором   элемента   матрицы  n-го  порядка называется определитель матрицы  (n-1)-го порядка, полученный из матрицы  А  вычеркиванием  i-й строки и  j-го столбца.

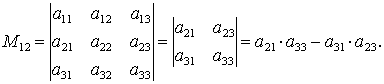
При выписывании определителя  (n-1)-го порядка, в исходном определителе элементы находящиеся под линиями в расчет не принимаются.

II. Алгебраические дополнения

Алгебраическим дополнением  А_ij  элемента а_ij матрицы  n-го порядка называется его минор, взятый со знаком, зависящим от номера строки и номера столбца:

то есть алгебраическое дополнение совпадает с минором, когда сумма номеров строки и столбца – четное число, и отличается от минора знаком, когда сумма номеров строки и столба – нечетное число.

3. Методы вычисления определителей

Свойства определителей второго порядка: Смотри вопрос 2

Определитель 2 порядка:

Определитель третьего порядка: правило треугольника и правило Саррюса. Правило треугольника: со знаком + берутся элементы, стоящие на главной диагонали и в вершинах треугольников, которые можно построить из элементов определителя с основаниями, параллельными главной диагонали. Со знаком «-» на побочной диагонали и аналогичных треугольниках. Правило Саррюса: таблица составляется из элементов определителя, присоединением к нему справа первых двух столбцов определителя. А11 а22 а33; а12 а23 а31; а13 а21 а32 – главные диагонали. А13 а 22 а 31; а11 а23 а32; а12 а21 а33 – побочные диагонали.