Определение векторного поля. Поле градиента. Потенциальные поля, условия потенциальности.
Векторное
поле. Если
каждой точке М
некоторой области V
пространства
соответствует значение некоторой
векторной величины
(M),
то говорят, что в области V
задано
векторное поле
(M).
Примеры векторных полей – поле тяготения,
поля электрической и магнитной
напряжённостей, поле скоростей частиц
движущейся жидкости.
Если
в некоторой декартовой системе координат
вектор
(M)
имеет координаты Р(M),
Q(M),
R(M),
то
.
Таким образом, задание векторного поля
(M)
эквивалентно заданию трёх скалярных
полей Р(M),
Q(M),
R(M).
Будем называть векторное поле гладким,
если его координатные функции - гладкие
скалярные поля.
Градиентом
дифференцируемого скалярного поля
u(M)=u(x,y,z) называется вектор
.
Т.е. сумма частных производных умноженных
на соответствующие единичные вектора.
В общем случае градиент вводится как векторная характеристика скалярного поля — то есть области, каждой точке которой соответствует значение определенного скаляра. Градиент характеризует, насколько быстро меняется скалярная величина в том или ином месте этого поля.
Потенциальные
векторные поля. Векторное
поле A = {Ax, Ay, Az} называется потенциальным,
если вектор А является градиентом
некоторой скалярной функции u = u(x, y,
z): A
= grad
u
= 
(16.7).
При этом функция u называется потенциалом данного векторного поля.
Выясним, при каких
условиях векторное поле является
потенциальным.
Так как из (16.7) следует, что
,
То
,
=
,
=
.
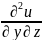так как смешанная производная второго
порядка не зависит от порядка
дифференцирования. Из этих равенств
легко получаем, что rot A = 0 -условие
потенциальности векторного поля.
Ротором
векторного поля
(M)
в точке
называется векторная величина (векторное
поле):
.
Если выразить
через оператор Гамильтона набла:
равен векторному произведению
.
Действительно,
.
Поток векторного поля через поверхность. Определение дивергенции векторного поля и её свойства. Вычисление дивергенции в декартовых координатах.
Поток
векторного поля через поверхность.
Пусть в области D
задано непрерывное векторное поле
,
.
Возьмем в этом векторном поле некоторую
поверхность S
и выберем ее определенную сторону. Пусть
– поле единичных нормалей к поверхности,
соответствующее выбранной стороне.
Тогда поверхностный интеграл 2-ого рода
(т.к.
)
называется потоком
вектора A
через поверхность S
в указанную сторону.
П
усть
.
Формула Гаусса-Остроградского:
Левую часть можно записать так: , , . Следовательно: , так как . Это поток вектора через замкнутую поверхность. Правую часть можно записать как дивергенцию (расходимость): .
Дивергенцией
векторного поля A
в точке MÎV
называется производная функции
по объему в этой точке:
.
Дивергенцию можно записать и с помощью
оператора
Набла:
.
Дивергенция
в декартовых координатах:
.
Свойства дивергенции:
.
.
Другие свойства (на лекции не разбирали, на усмотрение сдающего):
Если u – скалярное поле, а F – векторное:
.Свойство, связывающее векторные поля F и G, заданные в трёхмерном пространстве, с ротором:
.Дивергенция от ротора равна нулю:
.
Соленоидальные векторные поля, условия соленоидальности.
Пусть в некоторой
области D
задано непрерывное векторное поле
(M)=
(x,y,z).
Потоком
векторного поля
через ориентированную кусочно-гладкую
поверхность S,
расположенную в области D,
называется интеграл
,
где
– единичный
вектор нормали к поверхности S,
указывающий на ее ориентацию, а
– элемент
площади поверхности S.
Векторное поле называется соленоидальным в области D, если поток этого поля через любую кусочно-гладкую несамопересекающуюся поверхность, расположенную в D и представляющую собой границу некоторой ограниченной подобласти области D, равен нулю.
Е
сли
дивергенция равна нулю, то есть
,
то поле вектора
называется соленоидальным.
,
поэтому поток везде, на каждом сечении
трубки, одинаков.
Для того чтобы
непрерывно дифференцируемое векторное
поле
было соленоидальным
в объемно-односвязной области D,
необходимо и
достаточно,
чтобы во всех точках D
выполнялось равенство
.
Где дивергенцией (“расходимость”)
векторного поля
называется скалярная функция
