10. Формула Грина. Условия того, что криволинейный интеграл на плоскости не зависит от пути интегрирования.

Формула Грина: Если C – замкнутая граница области D и функции P(x,y) и Q(x,y) вместе со своими частными производными первого порядка непрерывны в замкнутой области D (включая границу C), то справедлива формула Грина: , причем обход вокруг контура C выбирается так, что область D остается слева.

И з лекций: Пусть заданы функции P(x,y) и Q(x,y), которые непрерывны в области D вместе с частными производными первого порядка. Интеграл по границе (L), целиком лежащий в области D и содержащий все точки в области D: 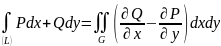. Положительное направление контура такое, когда ограниченная часть контура находится слева.

У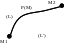 словие независимости криволинейного интеграла 2-го рода от пути интегрирования. Необходимым и достаточным условием того, что криволинейный интеграл первого рода, соединяющий точки M₁ и M₂, не зависит от пути интегрирования, а зависит только от начальной и конечной точек, является равенство: .

.

.

.

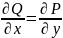11. О пределение поверхностного интеграла первого рода, его основные свойства и вычисление.

– задание поверхности.

Спроектируем S на плоскость xy, получим область D. Разобьём область D сеткой линий на части, называемые D_i. Из каждой точки каждой линии проведём параллельные z линии, тогда и S разделится на S_i. Составим интегральную сумму: . Устремим максимум диаметра D_i к нулю: , получим:

Это поверхностный интеграл первого рода

Так считается поверхностный интеграл первого рода.

Определение вкратце. Если существует конечный предел интегральной суммы, не зависящий от способа разбиения S на элементарные участки S_i и от выбора точек, то он называется поверхностным интегралом первого рода.

При переходе от переменных x и y к u и v:

Поверхностный интеграл обладает всеми свойствами обычного интеграла. См. в вопросах выше.

12. Определение поверхностного интеграла второго рода, его основные свойства и вычисление. Связь с интегралом первого рода.

П усть задана поверхность S, ограниченная линией L (рис. 3.10). Возьмём на поверхности S какой-нибудь контур L, не имеющий общих точек с границей L. В точке М контура L можно восстановить две нормали и к поверхности S. Выберем какое-либо одно из этих направлений. Обводим точку M по контуру L с выбранным направлением нормали.

Если в исходное положение точка M вернётся с тем же направлением нормали (а не с противоположным), то поверхность S называют двусторонней. Мы будем рассматривать только двусторонние поверхности. Двусторонней поверхностью является всякая гладкая поверхность с уравнением .

Пусть S – двусторонняя незамкнутая поверхность, ограниченная линией L, не имеющей точек самопересечения. Выберем определённую сторону поверхности. Будем называть положительным направлением обхода контура L такое направление, при движении по которому по выбранной стороне поверхности сама поверхность остаётся слева. Двусторонняя поверхность с установленным на ней таким образом положительным направлением обхода контуров называется ориентированной поверхностью.

Перейдём к построению поверхностного интеграла второго рода. Возьмём в пространстве двустороннюю поверхность S, состоящую из конечного числа кусков, каждый из которых задан уравнением вида или является цилиндрической поверхностью с образующими, параллельными оси Oz.

Пусть R(x,y,z) – функция, опредёленная и непрерывная на поверхности S. Сетью линий разбиваем S произвольным образом на n "элементарных" участков ΔS₁, ΔS₂, ..., ΔS_i, ..., ΔS_n, не имеющих общих внутренних точек. На каждом участке ΔS_i произвольным образом выберем точку M_i(x_i,y_i,z_i) (i=1,...,n). Пусть (ΔS_i)xy – площадь проекции участка ΔS_i на координатную плоскость Оху, взятая со знаком "+", если нормаль к поверхности S в точке M_i(x_i,y_i,z_i) (i=1,...,n) образует с осью Oz острый угол, и со знаком "–", если этот угол тупой. Составим интегральную сумму для функции R(x,y,z) по поверхности S по переменным x,y: . Пусть λ – наибольший из диаметров ΔS_i (i = 1, ..., n).

Если существует конечный предел , не зависящий от способа разбиения поверхности S на "элементарные" участки ΔS_i и от выбора точек , то он называется поверхностным интегралом по выбранной стороне поверхности S от функции R(x,y,z) по координатам х, у (или поверхностным интегралом второго рода) и обозначается .

Аналогично можно построить поверхностные интегралы по координатам x, z или у, z по соответствующей стороне поверхности, т. е. и .

Если существуют все эти интегралы, то можно ввести "общий" интеграл по выбранной стороне поверхности: .

Поверхностный интеграл второго рода обладает обычными свойствами интеграла. Заметим лишь, что любой поверхностный интеграл второго рода изменяет знак при перемене стороны поверхности.

Связь между поверхностными интегралами первого и второго рода.

Пусть поверхность S задана уравнением: z = f(x,y), причем f(x,y), f'_x(x,y), f'_y(x,y) — непрерывные функции в замкнутой области τ (проекции поверхности S на координатную плоскость Оху), а функция R(x,y,z) непрерывна на поверхности S. Нормаль к поверхности S, имеющая направляющие косинусы cos α, cos β, cos γ, выбрана к верхней стороне поверхности S. Тогда .

Для общего случая имеем:

=