Отметим ряд свойств функции Лапласа, полезных для применения.
1. Функция Ф(x) – нечетная, т. е. Ф(-x) = –Ф(x).
2. Функция
Ф(x) – возрастающая, быстро приближающаяся
к своему пределу, равному 0,5: Ф(0) = 0,
Ф(1) = 0,3413, Ф(2) = 0,4772, Ф(3) = 0,4986,
Ф(4) = 0,4999 и т.д. На практике полагают
Ф(x) 
для
x>5.
Правила двух и трех сигм |
Если в формуле (1) принять последовательно d = 2s и d = 3s, то получим:
Правило двух сигм. Почти достоверно (с доверительной вероятностью 0,954) можно утверждать, что все значения случайной величины X с нормальным законом распределения отклоняются от ее математического ожидания M(X) = a на величину, не большую 2s (двух средних квадратических отклонений).
Доверительной вероятностью Pд называют вероятность событий, которые условно принимаются за достоверные (их вероятность близка к 1). При решении вопросов, требующих большей надежности, когда доверительную вероятность принимают равной 0,997, вместо правила двух сигм, согласно формуле (3), используют правило трех сигм.
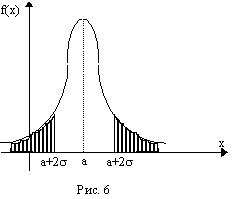
Проиллюстрируем правило двух сигм геометрически. На рис. 6 изображена кривая Гаусса с центром распределения а. Площадь, ограниченная всей кривой и осью Оx, равна 1 (100%), а площадь криволинейной трапеции между абсциссами а–2s и а+2s, согласно правилу двух сигм, равна 0,954 (95,4% от всей площади). Площадь заштрихованных участков равна 1-0,954 = 0,046 (»5% от всей площади). Эти участки называют критической областью значений случайной величины. Значения случайной величины, попадающие в критическую область, маловероятны и на практике условно принимаются за невозможные.
Вероятность
условно невозможных значений называют
уровнем значимости случайной величины.
Уровень значимости связан с доверительной
вероятностью формулой где q – уровень значимости, выраженный в процентах. Согласно правилу трех сигм при доверительной вероятности 0,997 критической областью будет область значений признака вне интервала (а-3s, а+3s). Уровень значимости составляет 0,3%. Уровень значимости принимают различным в зависимости от дозволенной степени риска. В текстильной и швейной промышленности его принимают равным 5%. С помощью правила двух (или трех) сигм можно определить общий интервал изменения той или иной случайной величины с нормальным законом распределения. |
(2)
(3)
= 1-
,
19. Теоремы Муавра-Лапласа
Пусть
в каждом из 
независимых
испытаний событие A может
произойти с вероятностью 
, 
(условия схемы
Бернулли).
Обозначим как и раньше, через 
вероятность
ровно 
появлений
события А в
испытаниях.
кроме того, пусть 
–
вероятность того, что число появлений
события А находится
между 
и 
.
Локальная теорема Лапласа.
Если n – велико, а р – отлично от 0 и 1, то
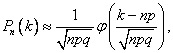где 
-
функция Гаусса (функция табулирована,
таблицу можно скачать на странице формул
по теории вероятностей).
Интегральная теорема Лапласа.
Если n – велико, а р – отлично от 0 и 1, то
P(n;
k1, k2)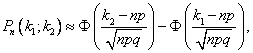
где 
-
функция Лапласа (функция табулирована,
таблицу можно скачать на странице формул
по теории вероятностей).
Функции Гаусса и Лапласа обладают свойствами, которые необходимо знать при использовании таблиц значений этих функций:
а) 
б)
при больших 
верно 
.
Теоремы
Лапласа дают удовлетворительное
приближение при 
.
Причем чем ближе значения 
к
0,5, тем точнее данные формулы. При
маленьких или больших значениях
вероятности (близких к 0 или 1) формула
дает большую погрешность (по сравнению
с исходной формулой Бернулли).