Основные теоремы о пределах.

Справедливы следующие основные теоремы о пределах.

Теорема 1. Пусть существуют (i=1,…, п). Тогда

Теорема 2. Пусть существуют и Тогда

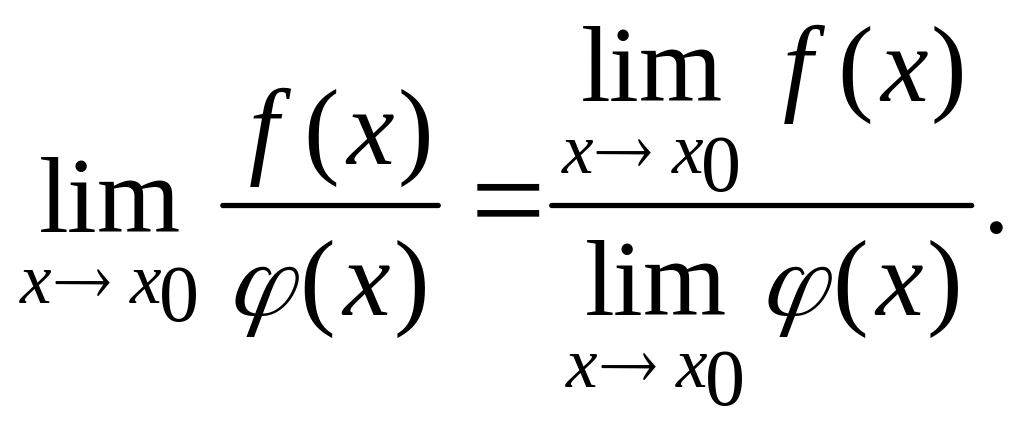
Эти утверждения сохраняются и при х₀ = .

Если условия этих теорем не выполняются, то могут возникнуть неопределенности вида - , , и др., которые в простейших случаях раскрываются с помощью алгебраических преобразований.

Замечательные пределы. Сравнение бесконечно малых функций. Широко используются следующие два предела

1)

2) ,

которые называются соответственно первым и вторым замечательными пределами.

Если (т. Е. для любого >0 существует число >0, такое что при 0< < справедливо неравенство < ), то называется бесконечно малой функцией или величиной при х .

Для сравнения двух бесконечно малых функций и при х находят предел их отношения

(1)

Если С 0, то и называются бесконечно малыми величинами одного и того же порядка; если С=0, то называется бесконечно малой более высокого порядка по сравнению с , а - бесконечно малой более низкого порядка по сравнению с .

Если (0< < ), то называется бесконечно малой порядка k, по сравнению с при х .

Если , то бесконечно малые и при х называются эквивалентными (равносильными) величинами и обозначают ~ .

Например, при х ~ , ~ х, ~ х, —1~ ..

Легко доказать, что предел отношения бесконечно малых функций и при х равен пределу отношения эквивалентных им бесконечно малых функций и при х , т.е. верны предельные равенства

Непрерывность функции. Классификация точек разрыва функции.

Функция у=f(х) называется непрерывной при х=x₀ (в точке x₀), если:

1. функция f(х) определена в точке x₀ и ее окрестности;

2. существует конечный предел функции f(х) в точке x₀;

3. этот предел равен значению функции в точке x₀ , то есть

(2)

Если положить х=x₀+ , то условие непрерывности (2) будет равносильно условию

т. Е. функция у=f(х) непрерывна в точке x₀ тогда и только тогда, когда бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции .

Функция, непрерывная во всех точках некоторой области, называется непрерывной в этой области.

Точка x₀, в которой нарушено хотя бы одно из трех условий непре­рывности функции, называется точкой разрыва функции. Если в точке x₀ существуют конечные пределы f(x₀-0) и f(x₀ +0), такие, что f(x₀-0) f(x₀+0), то x₀ называется точкой разрыва первого рода. Если хотя бы один из пределов f(x₀-0) и f(x₀+0) не существует или равен бесконечности, то точку x₀ называют точкой разрыва второго рода. Если f(x₀-0)=f(x₀ +0) и функция f(х) не определена в точке x₀, то точку x₀ называют устранимой точкой разрыва функции.

Свойства непрерывных функций:

1. Сумма, произведение и частное двух непрерывных функций есть непрерывная функция (при условии, что знаменатель отличен от нуля).

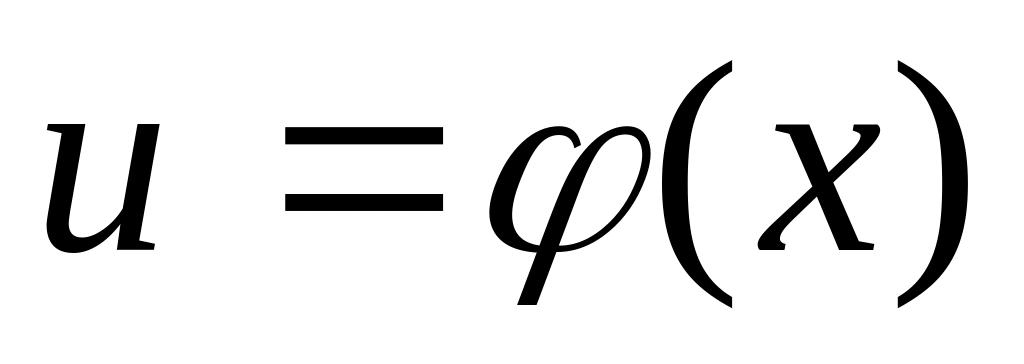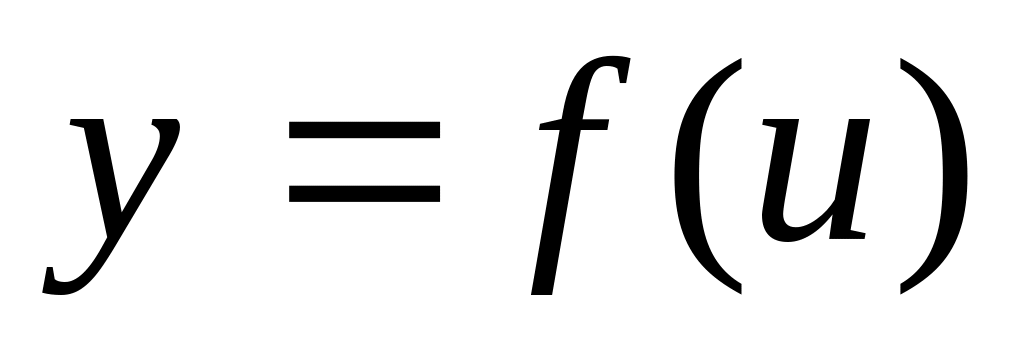2. Пусть функция непрерывна в точке , а функция непрерывна в точке . Тогда сложная функция непрерывна в точке .

3. Теорема 1 (Вейерштрасса). Если функция непрерывна на отрезке, то она ограничена на этом отрезке.

4. Теорема 2 (Вейерштрасса). Если функция непрерывна на отрезке, то она достигает на этом отрезке своего наибольшего и наименьшего значения.

5. Теорема 1 (Больцано-Коши). Если функция 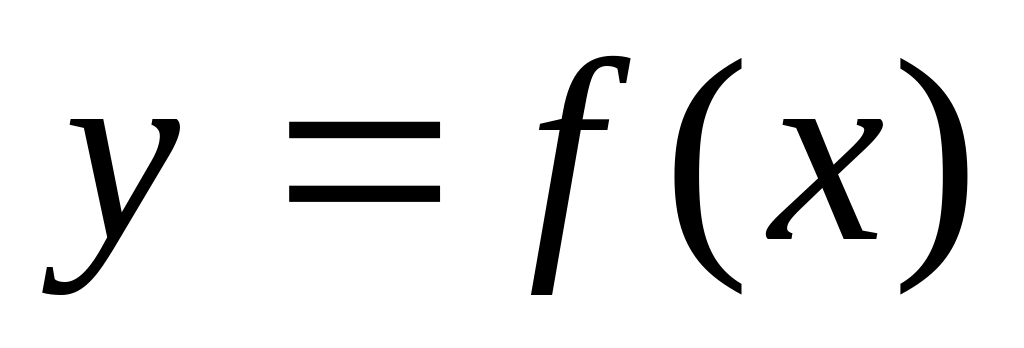непрерывна на отрезке 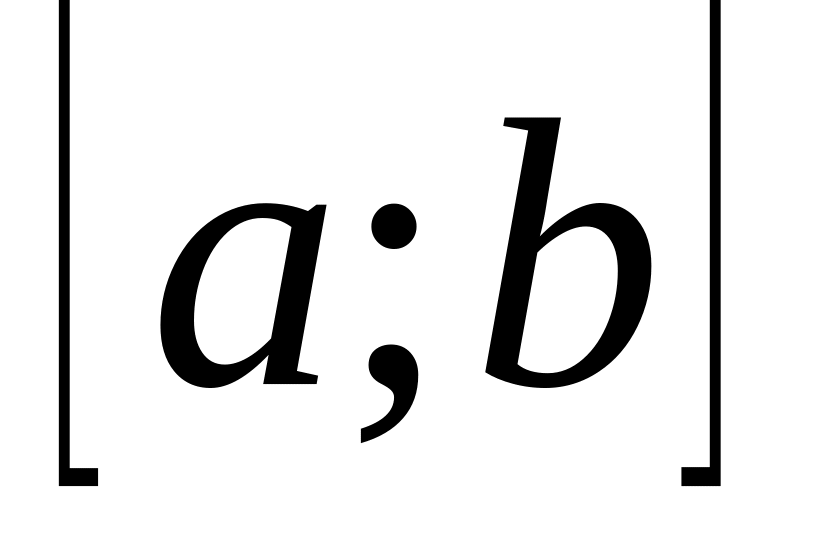и на его концах принимает значения разных знаков, то внутри отрезка найдется хотя бы одна точка c, в которой данная функция обращается в ноль.

Лекции 33-36.