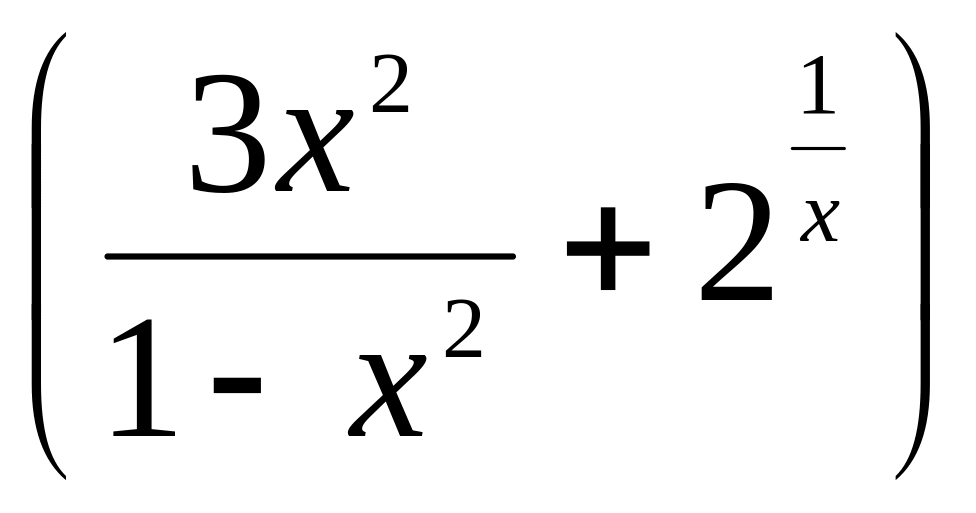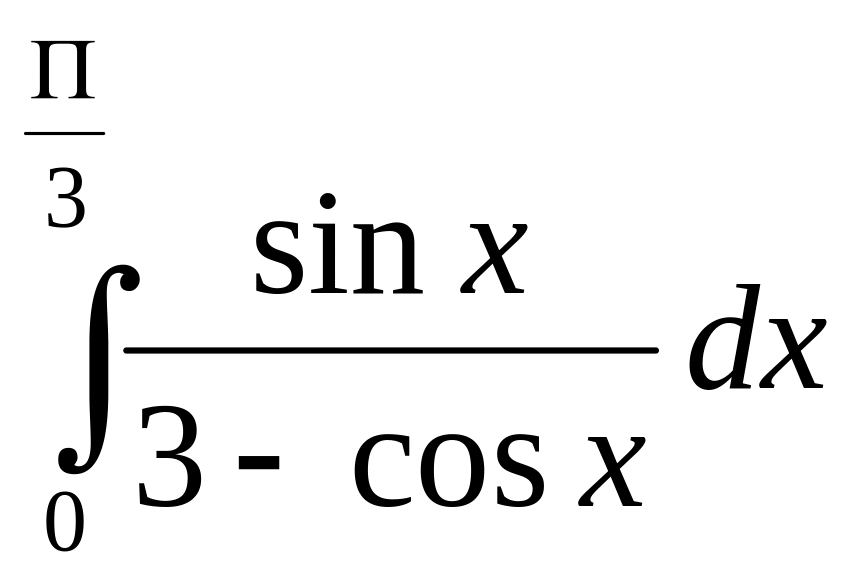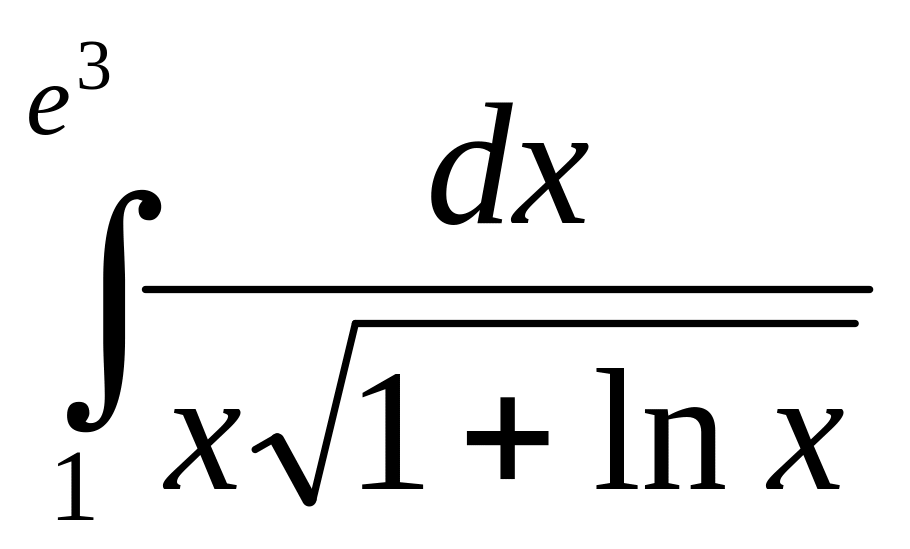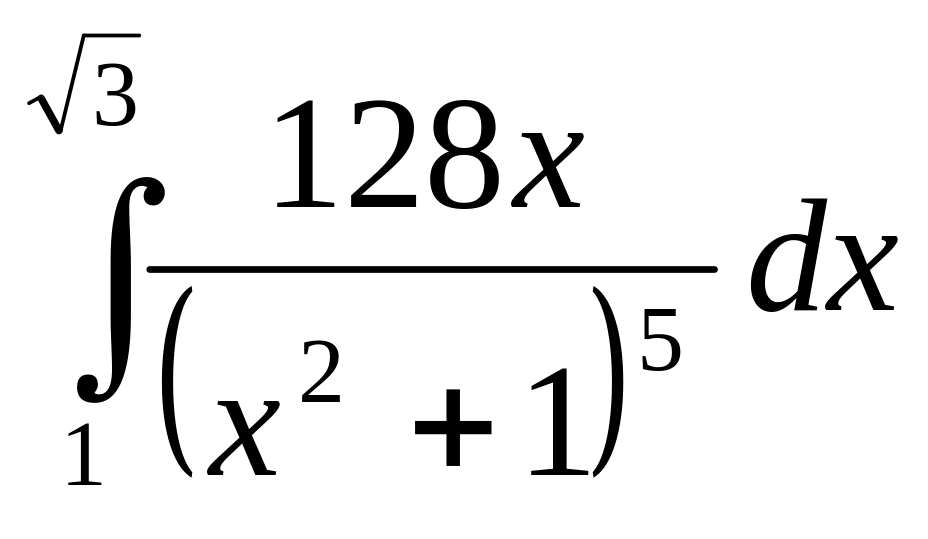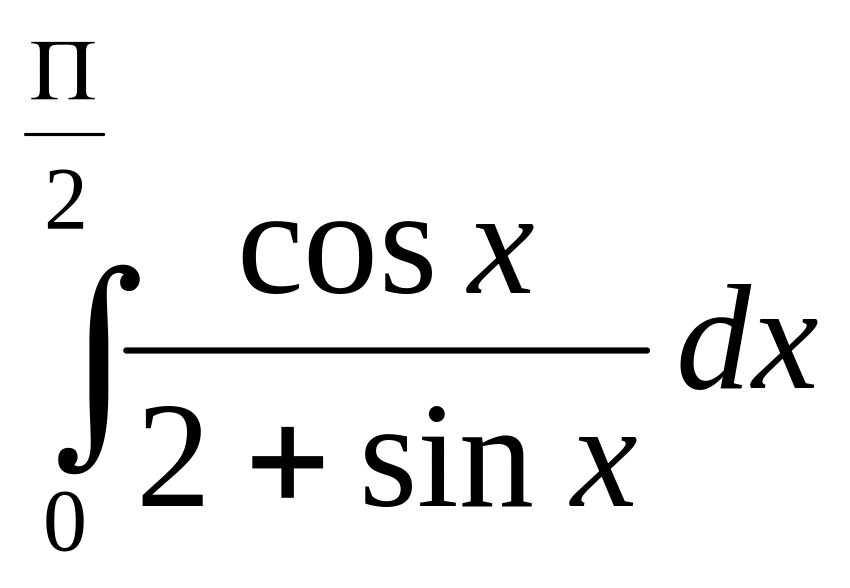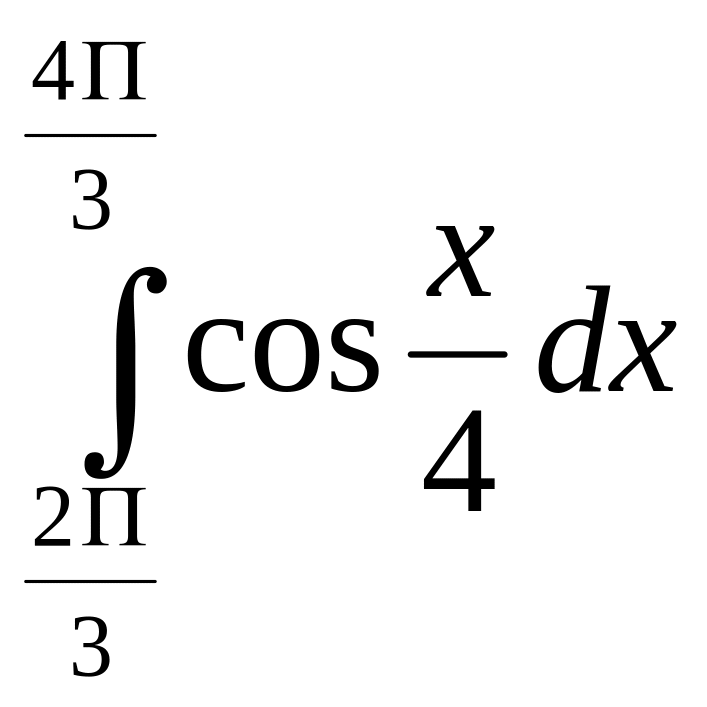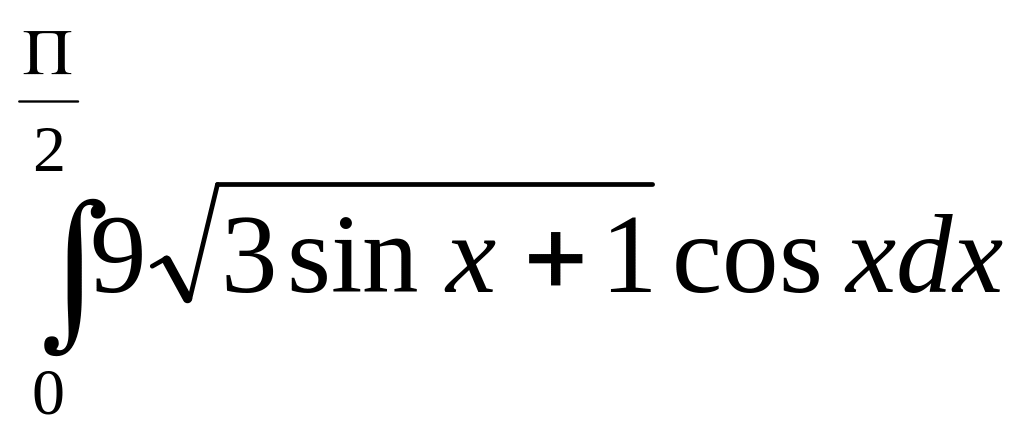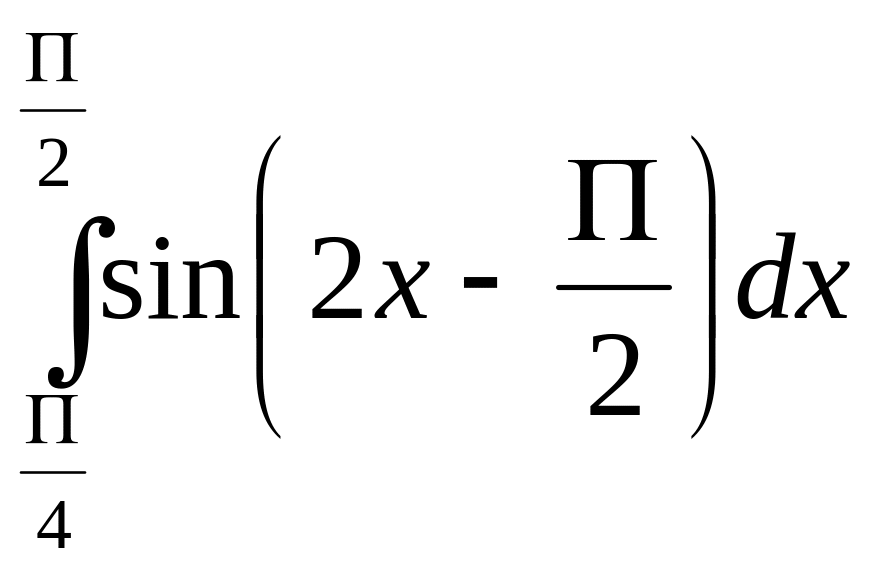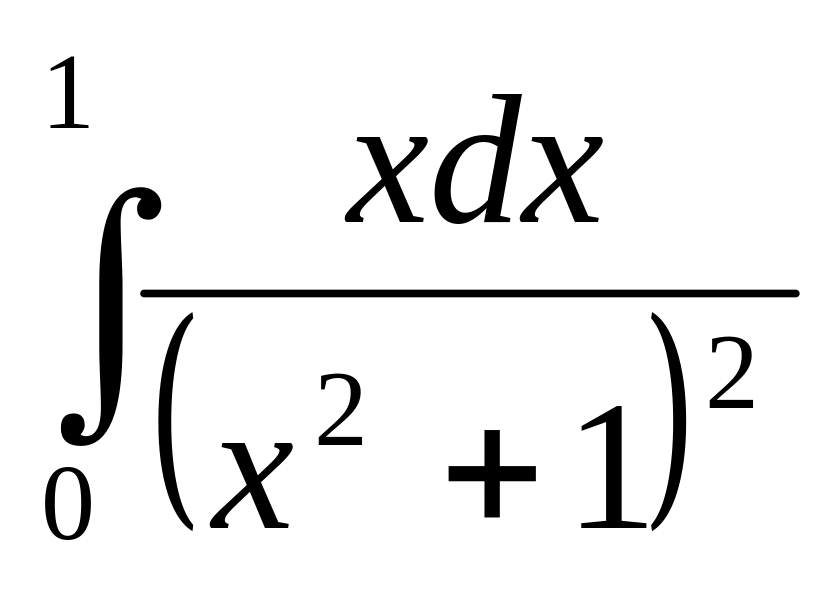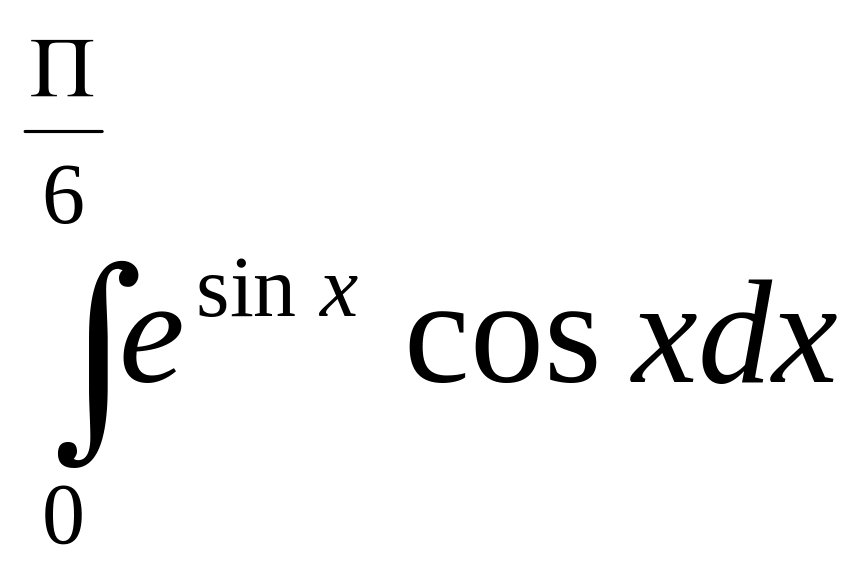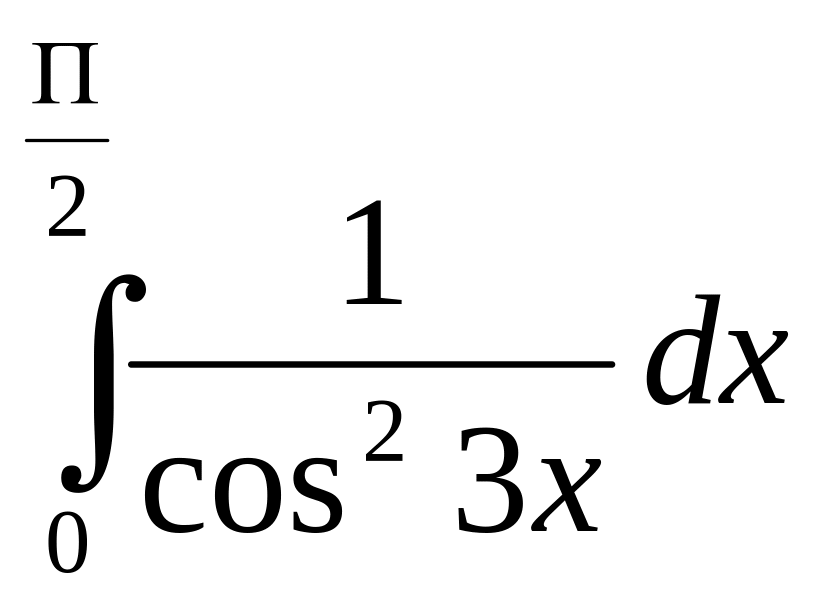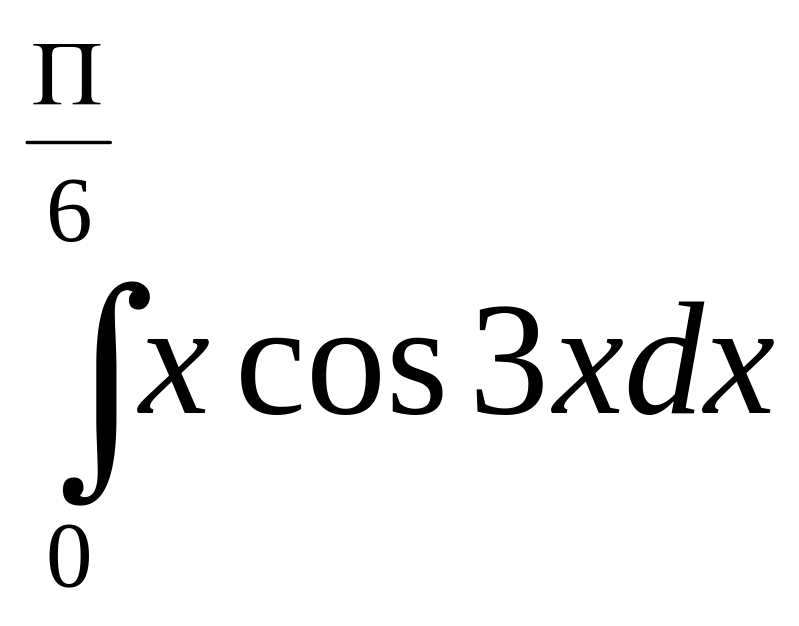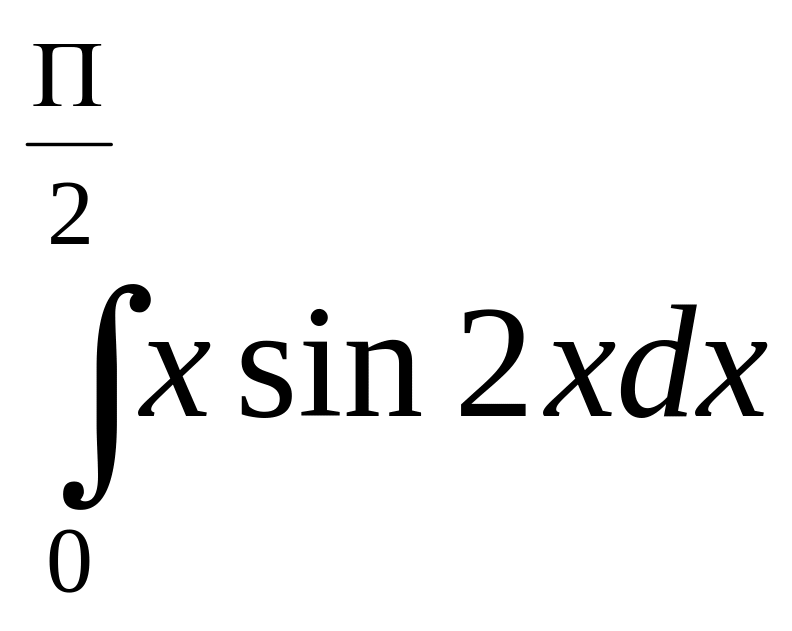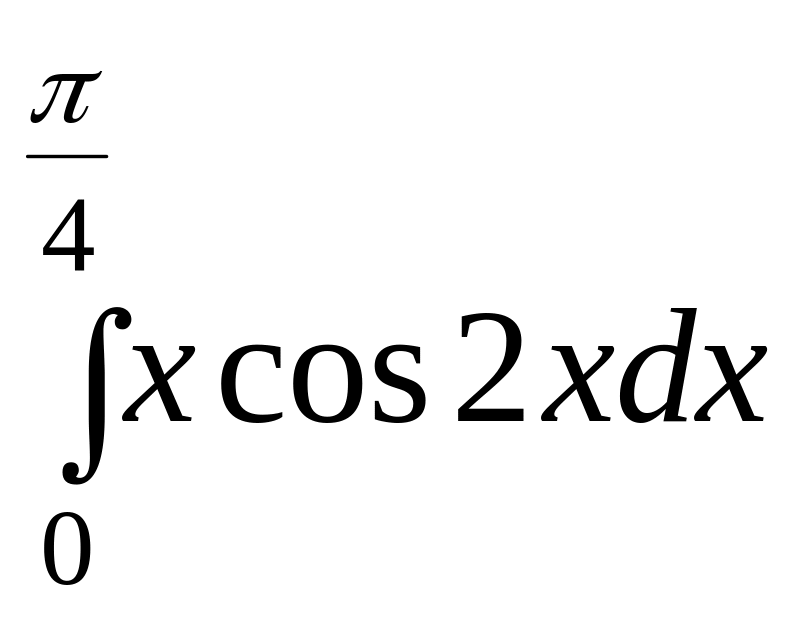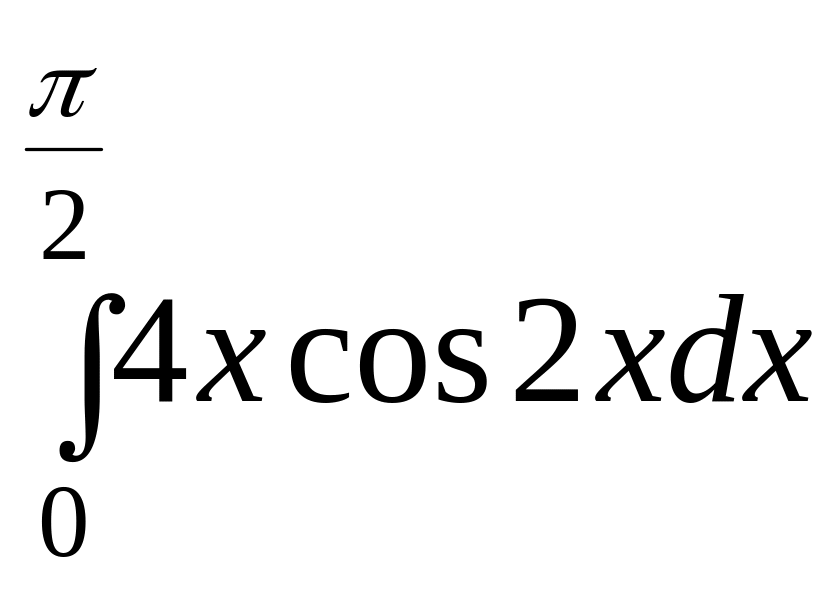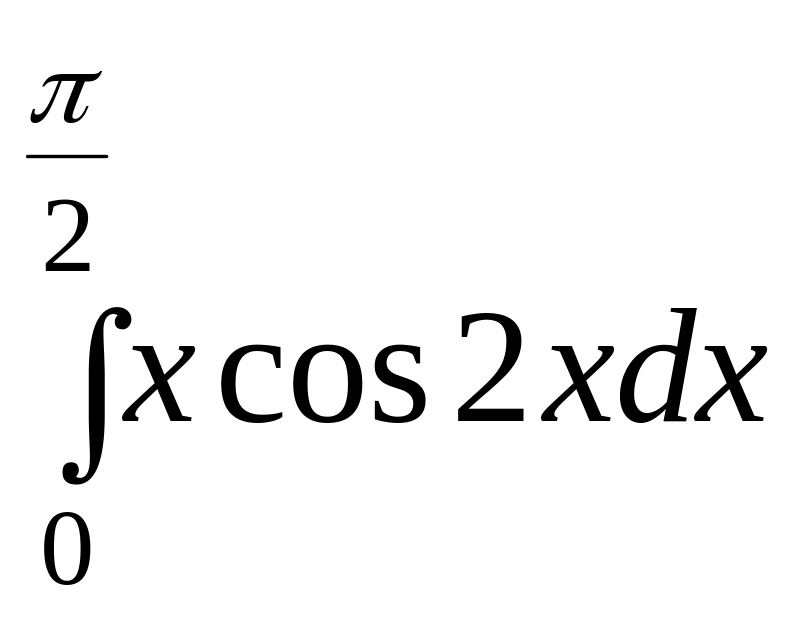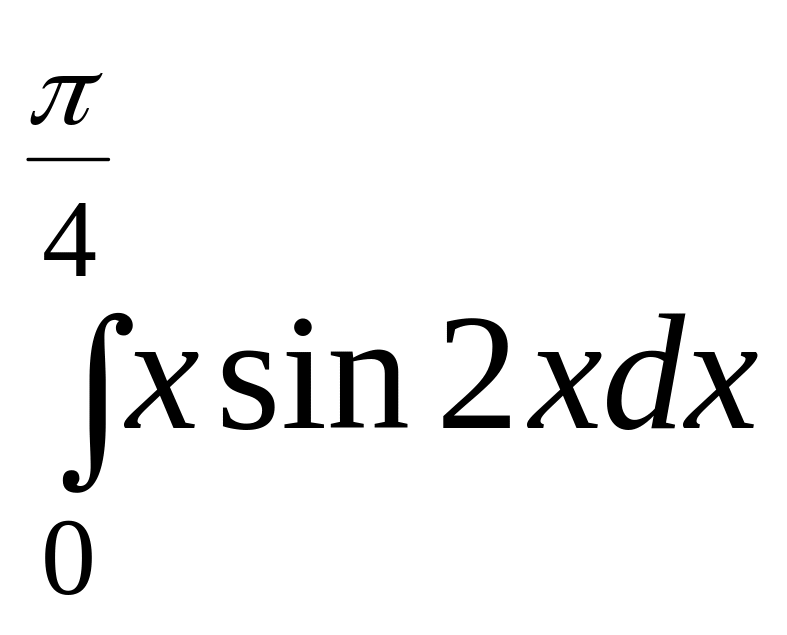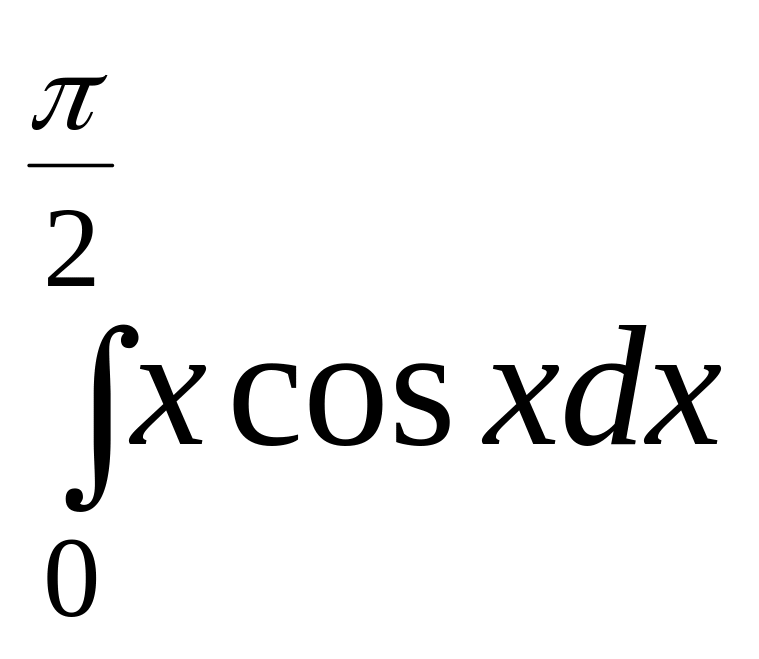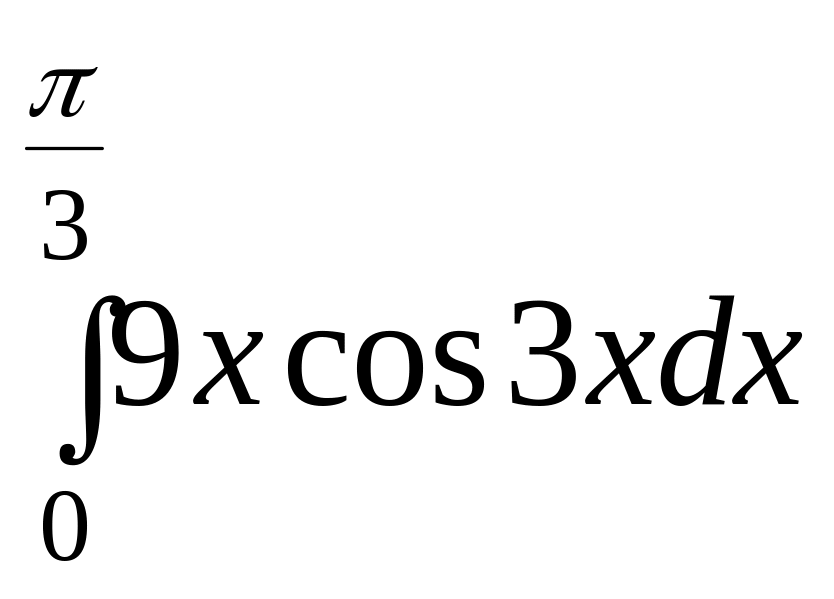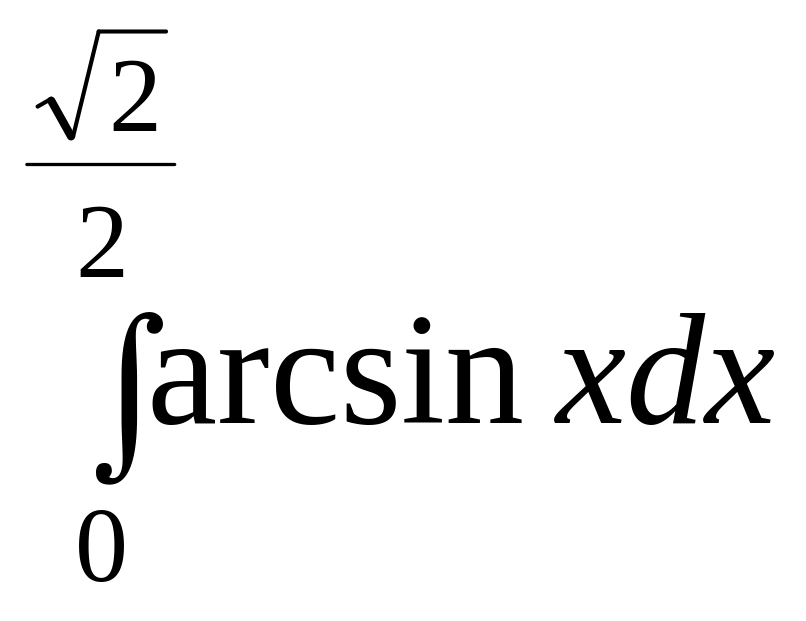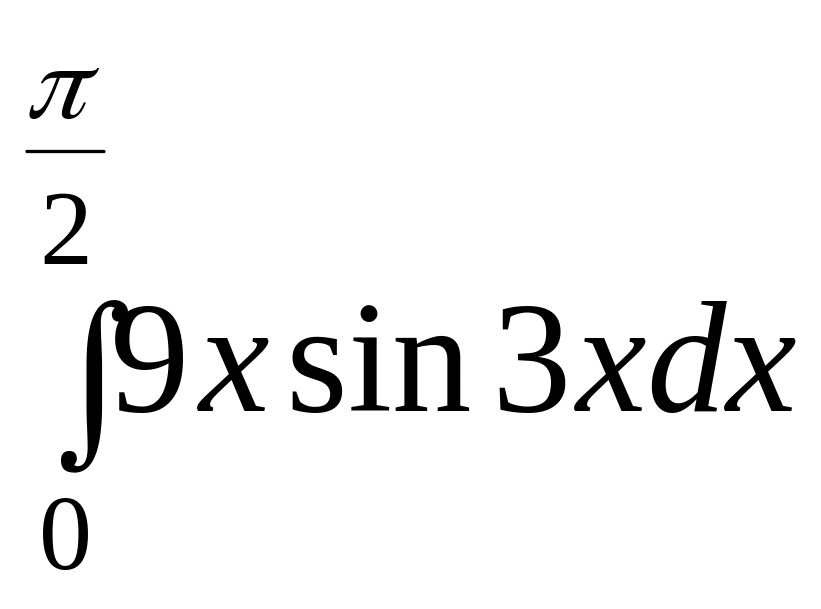- •Матрицы и операции над ними.
- •Определители.
- •Ранг матрицы
- •Системы линейных алгебраических уравнений.
- •Теорема Кронекера-Капелли
- •Формулы Крамера
- •Векторы, операции над ними.
- •Смешанное произведение векторов
- •Прямая на плоскости.
- •Кривые 2-го порядка.
- •Окружность.
- •Эллипс.
- •Гипербола.
- •Парабола
- •Уравнение плоскости.
- •Прямая в пространстве. Взаимное расположение прямой и плоскости в пространстве.
- •Функция. Действительные числа. Предел функции. Односторонние пределы функции.
- •Основные теоремы о пределах.
- •Замечательные пределы. Сравнение бесконечно малых функций. Широко используются следующие два предела
- •Непрерывность функции. Классификация точек разрыва функции.
- •Производная. Правила и формулы дифференцирования.
- •Производные высших порядков. Дифференциалы первого и высших порядков и их приложения.
- •Основные теоремы дифференциального исчисления (Ферма, Ролля, Лагранжа, Коши). Правило Лопиталя. Приложения производной и исследование функции.
- •Исследование поведения функции и построение их графиков.
- •Первообразная. Неопределенный интеграл и его свойства.
- •Интегрирование рациональных функций.
- •Интегрирование иррациональных и трансцендентных функций.
- •Определенный интеграл. Условия существования определенного интеграла. Свойства определенного интеграла.
- •Проведя в точках деления a,b прямые, параллельные оси ординат, разобьем криволинейную трапецию на n частичных трапеций. В каждом частичном интервале возьмем точки 1,2,…,т, так что
- •Оценка интеграла. Теорема о среднем. Формула Ньютона-Лейбница. Замена переменных и интегрирование по частям в определенном интеграле.
- •Приложения определенного интеграла.
- •Частные производные и дифференцируемость функций нескольких переменных.
- •Лекции 57-60. Дифференциальные уравнения. Дифференциальные уравнения I порядка.
- •Случайные события. Определение вероятности.
- •Вероятность достоверного события равна единице.
- •Теоремы сложения и умножения вероятностей. Формула полной вероятности. Формула Байеса.
- •Формула Бернулли. Предельные теоремы.
- •Случайные величины и их числовые характеристики.
- •Список рекомендуемой литературы Основная литература:
- •Дополнительная литература:
- •Планы проведения семинарских занятий.
- •Тема 1: Элементы линейной алгебры.
- •Тема 2: Элементы векторной алгебры.
- •Тема 3: Аналитическая геометрия
- •Тема 4: Функция. Предел функции.
- •Тема 5: Дифференциальное исчисление функции одной переменной.
- •Тема 6: Дифференциальное исчисление функции многих переменных
- •Тема 7: Интегральное исчисление.
- •Материалы для самостоятельной работы студента под руководством преподавателя (срсп)
- •Тема: «Предел функций».
- •Материалы по контролю и оценке учебных достижений студентов.
- •Тестовые задания для самоконтроля
- •Экзаменационные вопросы по курсу
Тема: «Предел функций».
Вычислить предел (табл.1).
Исследовать функцию (табл.2) и построить ее график.
Найти частные производные второго порядка функции многих переменных (табл.3).
Найти экстремумы функции двух переменных (табл.4).
Таблица 1. Варианты задания 1.
Вари-ант |
Предел |
Вари-ант |
Предел |
1 |
|
16 |
|
2 |
|
17 |
|
3 |
|
18 |
|
4 |
|
19 |
|
5 |
|
20 |
|
6 |
|
21 |
|
7 |
|
22 |
|
8 |
|
23 |
|
9 |
(1- |
24 |
|
10 |
|
25 |
|
11 |
|
26 |
|
12 |
|
27 |
|
13 |
|
28 |
|
14 |
|
29 |
|
15 |
|
30 |
|
Таблица 2. Варианты задания 2.
Вариант |
функция |
Вариант |
функция |
1 |
y= |
16 |
Y=
2 ln
|
2 |
y=x2 |
17 |
y= |
3 |
y=x+3 |
18 |
y=- (x+1)ex+2 |
4 |
y= |
19 |
y= |
5 |
y= |
20 |
y=2xln( |
6 |
y= |
21 |
y= |
7 |
y= |
22 |
y= |
8 |
y=3-3
ln
|
23 |
y=(x+1) |
9 |
y= |
24 |
y= |
10 |
y= |
25 |
y= |
11 |
y= |
26 |
y= |
12 |
y= |
27 |
y= |
13 |
y= |
28 |
y= |
14 |
y= |
29 |
y= |
15 |
y= |
30 |
y= |
Таблица 3. Варианты задания 3.
Вариант |
|
Вариант |
|
1 |
u= |
16 |
u= |
2 |
u= |
17 |
u= |
3 |
u=x2sin
|
18 |
u=y2xez |
4 |
u=ln (x2+y-2z) |
19 |
u=z sin x cos y |
5 |
u= |
20 |
U= |
6 |
u=xyez |
21 |
u= |
7 |
u=xz
tg |
22 |
u=z |
8 |
u=xyz |
23 |
u= |
9 |
u= |
24 |
u=xyz |
10 |
u=yz |
25 |
u= |
11 |
u=xy
cos
|
26 |
u=zyex |
12 |
u=x ln (y+z) |
27 |
u=xy ctg |
13 |
u= |
28 |
u= xy ln (y-z) |
14 |
u=x2zey |
29 |
u= |
15 |
u=x arctg yz |
30 |
u=yex+z |
Таблица 4. Варианты задания 4.
Вариант |
|
Вариант |
|
1 |
z=2x3+6xy2-30x-24y |
16 |
z= |
2 |
z=x3-y3 |
17 |
z= |
3 |
z=6x2y+2y3-24x-30y |
18 |
z= |
4 |
z=x3- 8y3- 6xy+1 |
19 |
z= |
5 |
z=x3- xy2+3x2+y2-1 |
20 |
z=- |
6 |
z=x2y- |
21 |
z=2y |
7 |
z=x3+6xy+3y2- 18x-18y |
22 |
z=x2- 4x - 2x+5y |
8 |
z=x2y- y3- x2- 3y2+3 |
23 |
z= |
9 |
z=3x2- 6xy - y3- 12x+12y |
24 |
z=2x2+3xy+2y3+5x |
10 |
z=2x3- xy2+5x2+y2 |
25 |
z=x3- 5xy+5y2+7x- 15y |
11 |
z=x2y - 2y3- x2- 5y2 |
26 |
z=2x2- 5xy+2y3- 3x+4y |
12 |
z= 2x3+y2+6xy+12x |
27 |
z=3x2+10xy+6y3+2x+2y-1 |
13 |
z=8x3- y3- 12xy - 1 |
28 |
z=3x3+7xy- |
14 |
z=2x3- 12x2y+16y3- 9x2 |
29 |
z=3x2- 2y +0.5y2- 56x |
15 |
z=-8x3+6xy2+y3+9y2 |
30 |
z=-2x3+3x +18x – 1,5y |
Тема: Интегралы.
Задание 1. Определить действительную и мнимую часть комплексного числа z.
Задание 4. Вычислить неопределенной интеграл и результата проверить дифференцированием.
Задание 3. Вычислить неопределенный интеграл.
Задание 4. Найти неопределенный интеграл.
Задание 5. Найти неопределенный интеграл.
Задание 6. Найти неопределенный интеграл.
Задание 7. Найти определенный интеграл.
Задание 8. Найти определенный интеграл.
Тема: Применение определенных интегралов.
Задание 1. Вычислить площадь фигуры, ограниченной кривыми
1 .1.у=3x, x²=3y.
1.2.y=3x²+1, y=3x+7
1.3.y=
![]() x²,y=
x²,y=
![]()
1.4.y=lnx, y=0, x=e
1.5.y=![]() x²,
y=
x²,
y=![]() , x=4
, x=4
1.6.
![]()
1.7.
![]()
1.8.
![]()
1
.9.
![]()
1.10.
![]()
1.11. p=4sin 2φ.
1.12. p=2cos 3φ.
1.13. y=3-2x-x², x²=-2y-1.
1.14.
y=![]() x²-2x-4, y=
x²-2x-4, y=![]() .
.
1.15.
y=![]() x²-2x+2, x+2y-8=0.
x²-2x+2, x+2y-8=0.
1.16.
y=
x²-1, y=8-![]() x².
x².
1.17. x=y², x= y²+1.
1.18.
![]()
1.19.
![]()
1.20.
![]()
1.21.
![]()
1.22.
![]()
1.23. p=cos 2φ
1.24. p=4 sinφ.
1.25. p=3 cosφ.
1.26. p=cos φ4
1.27. p=sin 3φ.
1.28. p²=cos 2φ
1.29. p=2 sin 4φ
1.30. p=4 sin²φ
Задание 2. Определить длину дуги, заданной кривими на данном отрезке.
2
.1.
![]() ,
,
![]() ≤
φ
≤
.
≤
φ
≤
.
2.2. p=8 cosφ , 0≤ φ ≤ π .
2.3.
![]() ,
,
![]() ≤
φ
≤
.
≤
φ
≤
.
2.4.
p=3e
³ , 0 ≤ φ
≤
![]() .
.
2.5. p=5(1cos φ), 0 ≤ φ ≤ .
2.6.
p=2
cos
φ
, 0 ≤ φ
≤
![]() .
.
2.7.
![]() ,
0 ≤ φ
≤
.
,
0 ≤ φ
≤
.
2.8. p=6sin φ, 0 ≤ φ ≤
2.9. p=2sin φ, 0 ≤ φ ≤
2.10. p=3(1-sin φ), 0 ≤ φ ≤
2
.11.
y=![]() , 0 ≤ x
≤ 5
, 0 ≤ x
≤ 5
2.12. y=ln(x²-1), 2 ≤ x ≤ 3.
2
.13.
y=ln
x,
![]() ≤
x
≤
≤
x
≤![]()
2.14.
y=ln
7-ln
x,
≤ x
≤
![]()
2.15.
y=![]() , 2 ≤ x
≤ 6
, 2 ≤ x
≤ 6
2.16. y=-ln cosx, 0 ≤ x ≤
2.17.
y=![]() –
–![]() lnx,
1 ≤ x
≤ e
lnx,
1 ≤ x
≤ e
2.18. y=1-ln sinx, ≤ x ≤
2.19. y=ln cosx, 0 ≤ x ≤
2
.20.
y=
ln![]() ,
≤ x
≤
,
≤ x
≤
2.21.
![]()
2.22.
![]()
2.23.
![]()
2.24.
![]()
2.25.
![]()
2.26.
2.27.
![]()
2.28.
![]()
2.29
![]()
2.30.
![]()
Задание
3.
Определить объем тела, полученной
поворотом фигуры образованной
пересечением кривых заданных уравнениями
![]() ,
,
![]() через ось Ox
(варианты 1-15), Oy
(варианты
16-30).
через ось Ox
(варианты 1-15), Oy
(варианты
16-30).
3.1. y=x², y=
3.2. y=x², y=2x
3.3. y=-2x-x², y=0
3.4. y=x²-2x+1, x=2, y=0
3.5. y= -x²+5x-6, y=0
3.6.
y=cosx, y=0, x=![]() ,
x=
,
x=![]()
3 .7. y=3sinx, y=sinx
3 .8. 2x-x²-y=0, 2x²-4x+y=0
3.9. y=x², y=1, x=2
3.10. y=2x-x², y= -x+2, x=0
3.11. y=2x-x², y= -x+2
3.12. y=x³, y=
3.13. y=lnx, x=2, y=0.
3.14. y=x², x=2, y=0.
3.15. y=(x-1)², x=0, x=2, y=0.
3.16. y=x³, y=x².
3.17. y=x², x+y-2=0, x=0.
3.18. y= , y=0, x=1.
3.19. y=x³, x=1, y=0.
3.20. x=5-y², x= -4y.
3.21. y²=x-1, x=5-y².
3.22..3x-2y+6=0, x=0, y=0.
3.23. x=y²-4y, x=0, y≤3.
3.24..xy=4, y=1, x=0, y=1, y=6
3.25.
y=![]() ,
y=
,
y=
![]() ,
x=16
,
x=16
3.26. y=x³, y=3x²
3.27. y=x³, y=x
3.28.
y=
, y=![]() ,
x=16
,
x=16
3.29. y=2x-x²+3, y=x²-4x+3.
3.30. x=8-y², x=-2y.