Интегрирование рациональных функций.

Важный класс функций, интегралы от которых всегда выражаются через элементарные функции, образуют рациональные функции, то есть функции, которые можно представить в виде дроби

где P(x), Q(x) – многочлены.

Если степень многочлена в числителе равна или больше степени многочлена в знаменателе, то, выполнив деление, получим

где W(x) – некоторый многочлен, а R(x) – многочлен степени ниже, чем Q(x).

Пример.

Многочлен W(x) представляет собой линейную комбинацию целых неотрицательных степеней x и поэтому может быть проинтегрирован. Теперь рассмотрим вопрос интегрирования правильной дроби из последнего соотношения.

Знаменатель правильной дроби разлагается на множители вида и а дробь разлагается на сумму элементарных дробей следующим образом

Интегралы данных дробей приводятся к интегралам следующего вида

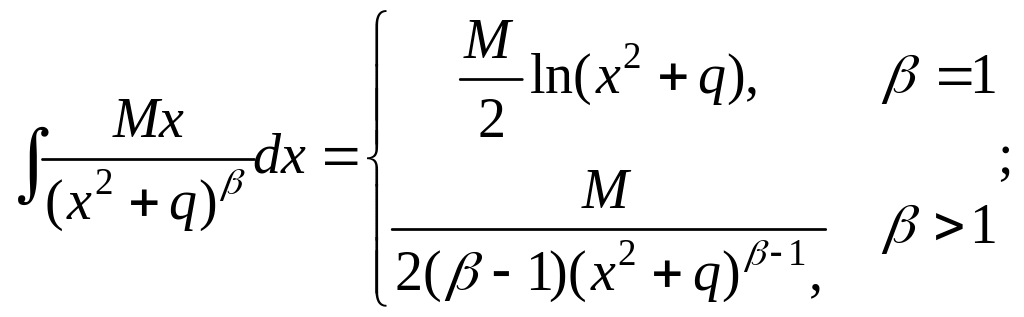
Интеграл вычисляется по рекуррентной формуле

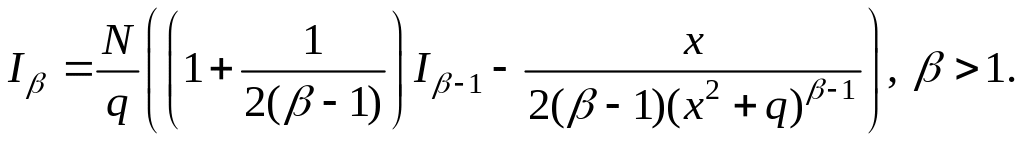
Таким образом, можно сделать вывод о том, что всякая рациональная функция может быть проинтегрирована в элементарных функциях.

Интегрирование иррациональных и трансцендентных функций.

Предварительно введем понятие рациональной функции от двух переменных u и v, то есть функции получающейся из этих переменных и некоторых постоянных, над которыми производятся только операции сложения, вычитания, умножения и деления R(u, v). Такова, например, функция

Если переменные u и v, в свою очередь являются функциями переменной x: то функция называется рациональной функцией от и

Рассмотрим теперь интегралы от некоторых простейших иррациональных и трансцендентных функций сводящихся к интегралам от рациональных функций.

1. Интегралы вида 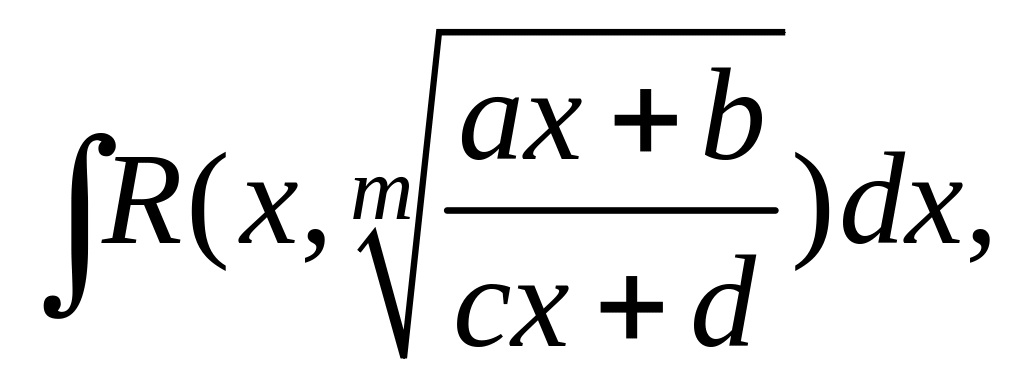где a, b, c, d – некоторые числа 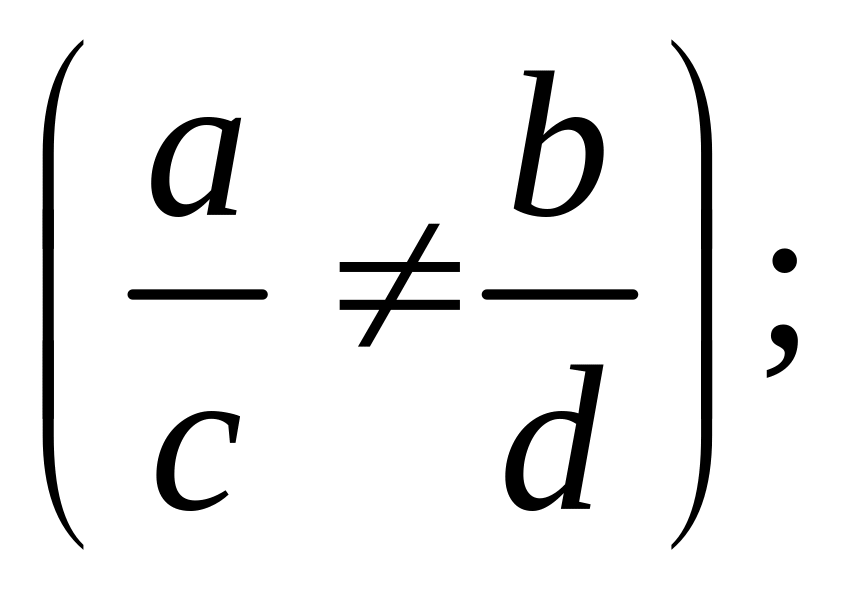m – натуральное число. Интегралы данного вида рационализируются подстановкой

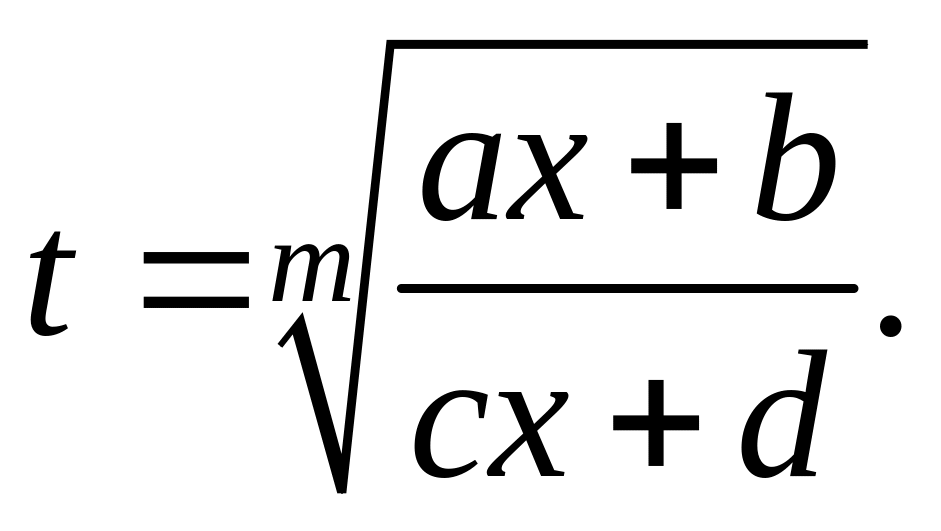
2. Интеграл вида 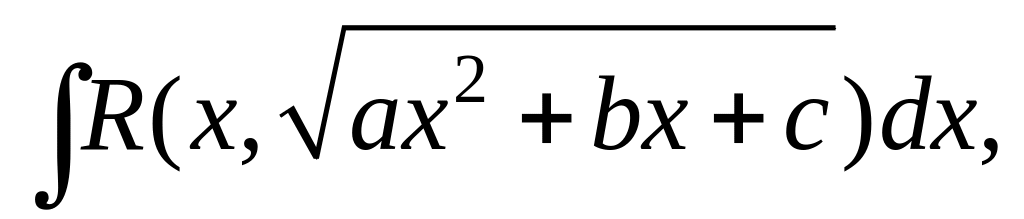где a, b, c – некоторые числа Данный интеграл зависит от корней квадратного трехчлена 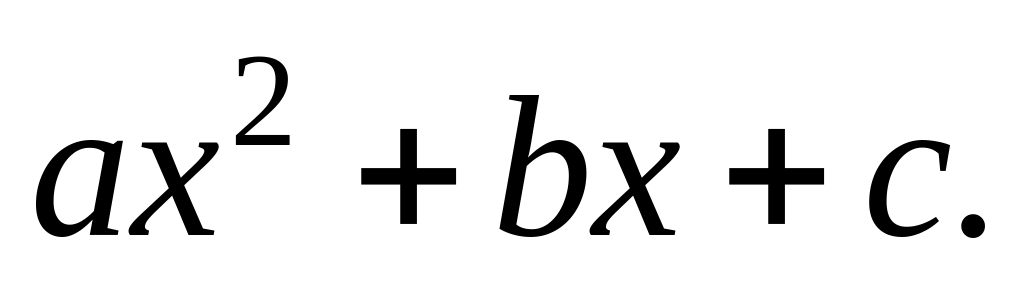Если этот трехчлен имеет два различных действительных корня x₁ и x₂, то он сводится к интегралу вида 1, а именно к интегралу

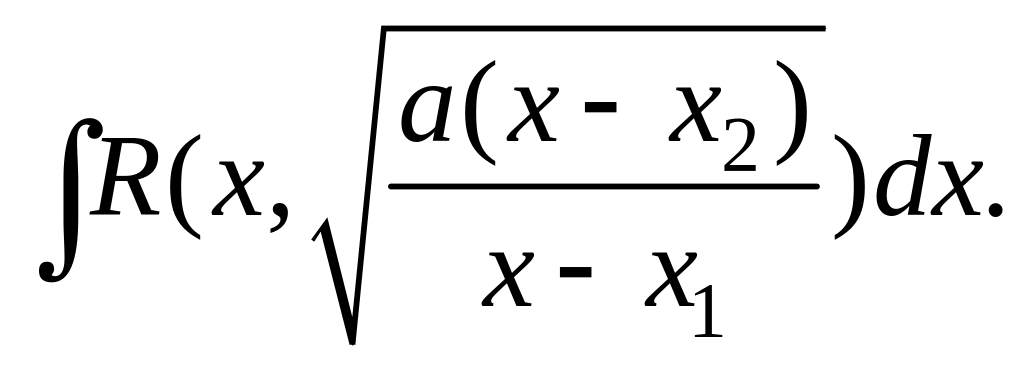
Если x₁=x₂, то интеграл сводится к интегралу от рациональной функции, а именно к интегралу

Если же квадратный трехчлен не имеет вещественных корней, то с помощью подстановки Эйлера

данный интеграл приводится к интегралу от рациональной функции

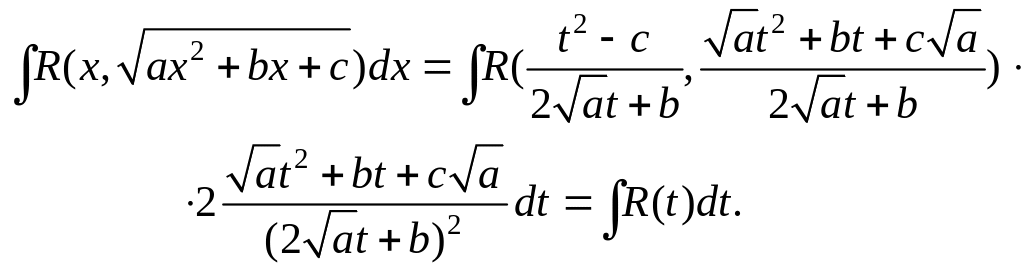
3. Интеграл вида 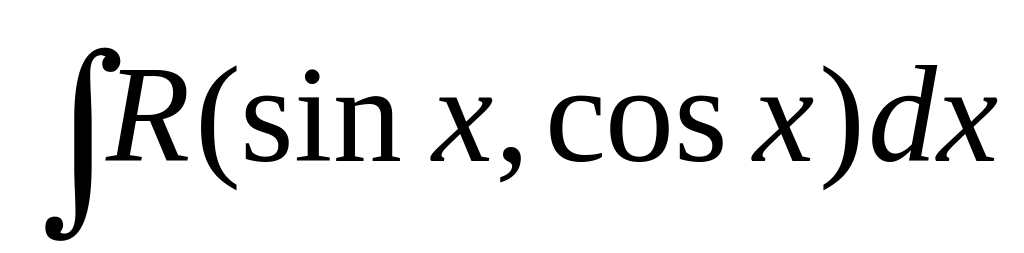рационализируется подстановкой 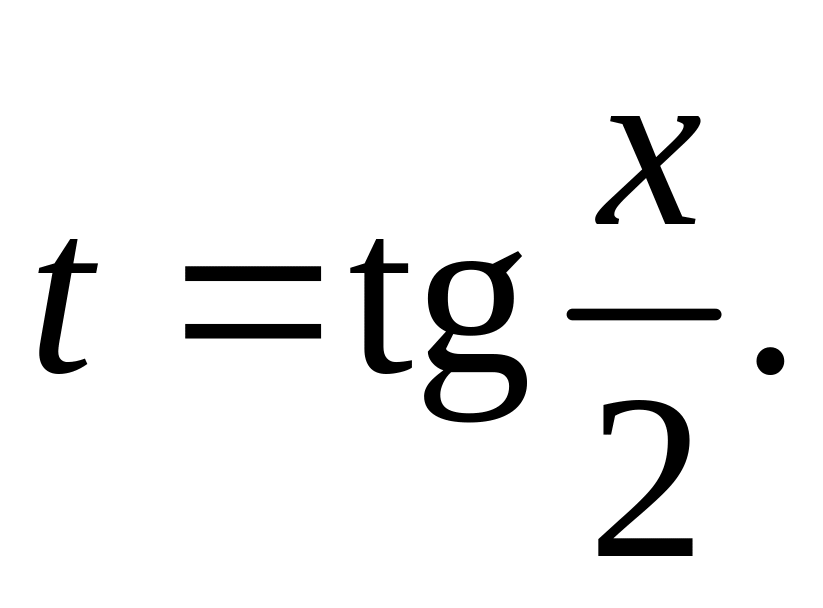Действительно,

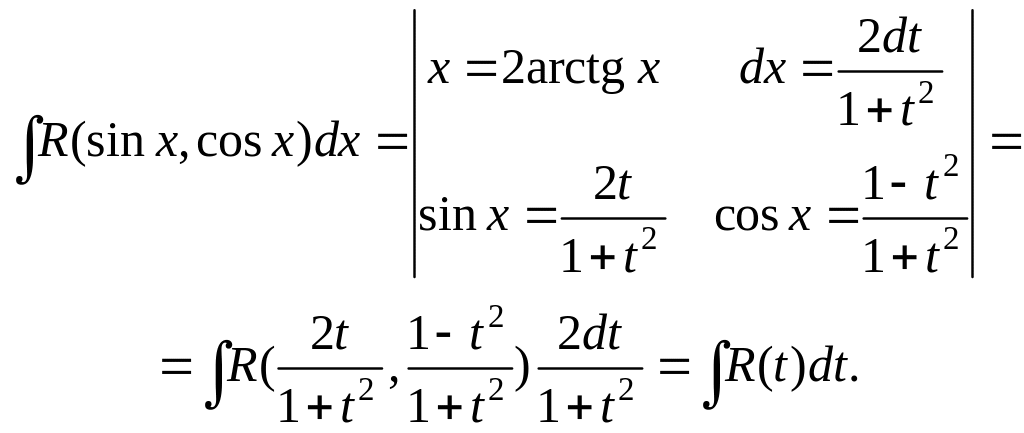
4. Интеграл вида 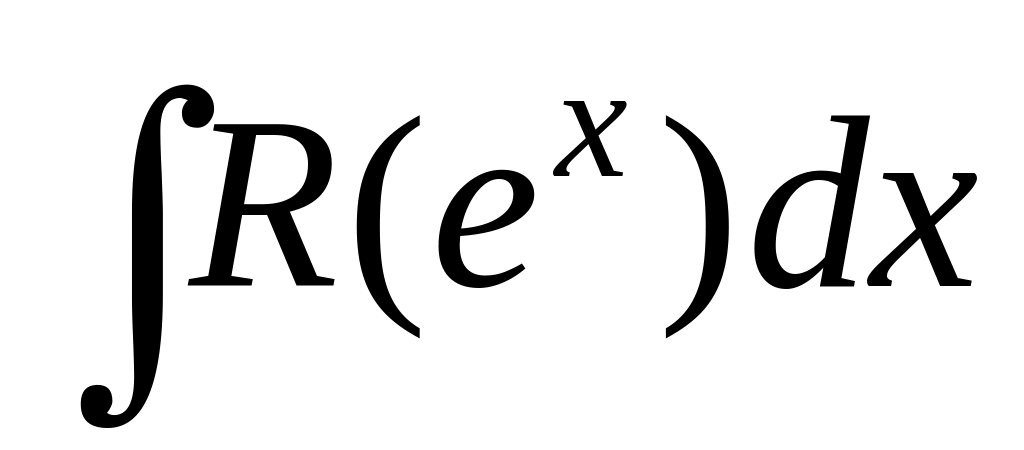рационализируется подстановкой 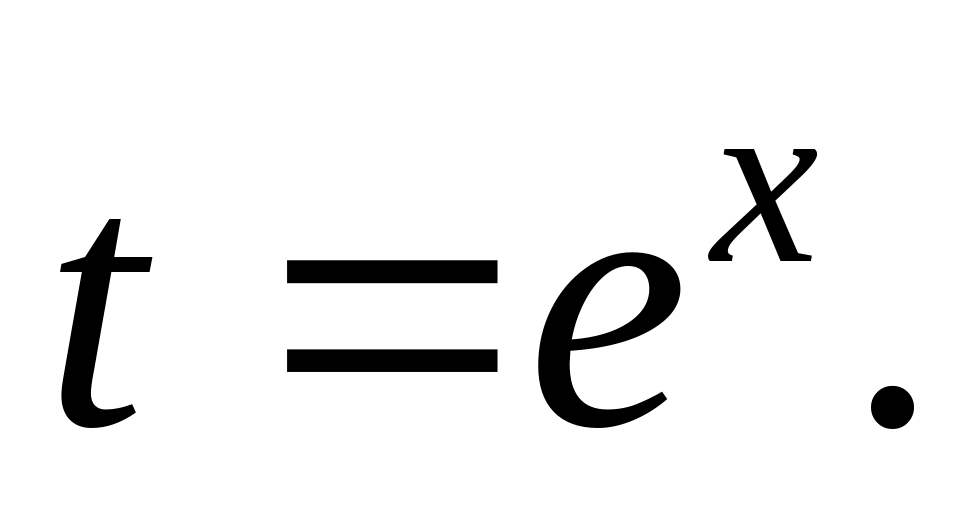Действительно,

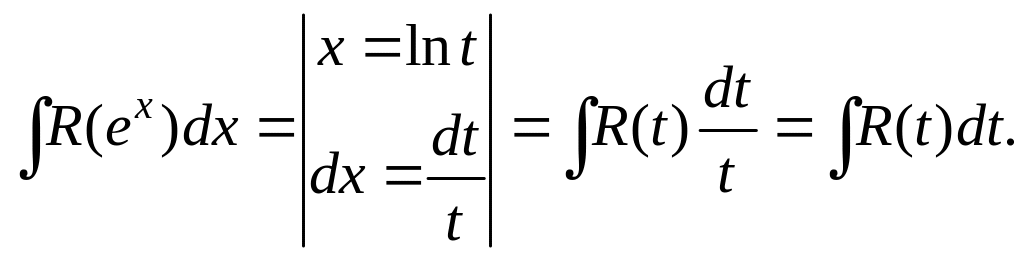
Лекции 49-52.

Определенный интеграл. Условия существования определенного интеграла. Свойства определенного интеграла.

Задача о поиске площади криволинейной трапеции приводит к понятию определенного интеграла. Криволинейная трапеция ограничена осью Ох, непрерывной функцией y=f(x), прямыми x=a и x=b, т.е. трапеция расположена над осью Ох. Разделим основание трапеции  интервал a,b на n частичных интервалов x₀,x₁,x₁,x₂,…,x_n-1,x_n, где a=x₀x₁x₂…x_n-1x_n=b.

Проведя в точках деления a,b прямые, параллельные оси ординат, разобьем криволинейную трапецию на n частичных трапеций. В каждом частичном интервале возьмем точки 1,2,…,т, так что

x₀₁x₁, x₁₂x₂, …, x_n-1_nx_n.

Рассмотрим значения ₁,₂,…,_n) и т.д.

В результате, сложив площади всех частичных трапеций, получим площадь криволинейной трапеции

S= S_n= _ix_i, где x_i=x_i-x_i-1.

_ix_i называется n-й интегральной суммой.

_ix_i= xdx называется определенным интегралом, a-нижний предел интегрирования, b- верхний предел интегрирования.

Определенным интегралом называется предел, к которому стремится интегральная сумма при стремлении к нулю длины наибольшего частичного интервала.

Теорема существования определенного интеграла. Если функция (x) непрерывна в замкнутом интервале a,b, то ее n-я интегральная сумма стремится к пределу при стремлении к нулю длины наибольшего частичного интервала. Этот предел, т.е. определенный интеграл xdx, не зависит от способа разбиения интервала интегрирования на частичные интервалы и от выбора в них промежуточных точек.

Свойства определенного интеграла.

Теорема 1 (об интеграле суммы). Интеграл от суммы конечного числа функций равен сумме интегралов от слагаемых функций:

_,

где u,v,…,w – функции независимой переменной x.

Теорема 2 (о вынесении постоянного множителя). Постоянный множитель подынтегральной функции можно вынести за символ интеграла:

,

где u – функция аргумента x, с – константа.

Теорема 3 (о перестановке пределов). Если верхний и нижний пределы интеграла поменять местами, то интеграл изменит только знак:

.

Если a=b, то , так как .

Теорема 4 (о разбиении интервала интегрирования). Если интервал интегрирования a,b разбит на две части a,c и c,b, то

.