Министерство образования и науки РФ

Федеральное агентство по образованию ГОУ ВПО

Всероссийский заочный финансово-экономический институт

Кафедра высшей математики

КОНТРОЛЬНАЯ РАБОТА

по дисциплине

ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МЕТОДЫ И ПРИКЛАДНЫЕ МОДЕЛИ

Пенза - 2011

ЗАДАЧА 1

Решить графическим методом типовую задачу оптимизации

При производстве двух видов продукции используется 4 типа ресурсов. Норма расхода ресурсов на производство единицы продукции, общий объем каждого ресурса заданы в таблице:

Ресурсы	Норма затрат ресурсов на товары		Общее количество ресурсов
	1-го вида	2-го вида
1	2	2	12
2	1	2	8
3	4	0	16
4	0	4	12

Прибыль от реализации одной единицы продукции первого вида составляет 2 ден. ед., второго вида – 3 ден. ед.

Задача состоит в формировании производственной программы выпуска продукции, обеспечивающей максимальную прибыль от ее реализации.

Требуется:

Построить экономико-математическую модель задачи, дать необходимые комментарии к ее элементам и получить решение графическим методом. Что произойдет, если решать задачу на минимум и почему?

Решение:

Обозначим количество двух выпускаемых видов продукции через х₁ и х₂ соответственно. Тогда прибыль, получаемая от реализации продукции, будет задаваться целевой функцией:

Число ограничений задачи равно числу ресурсов, необходимых для изготовления изделий – 4. Дополнительно вводим условие неотрицательности переменных. Зная нормы их расхода продукции и запасы ресурсов, можно сформулировать математическую модель задачи линейного программирования:

Прямые ограничения означают, что область решений будет лежать в I четверти декартовой системы координат. Определим область допустимых решений первого неравенства . Оно состоит из решения уравнения и строгого неравенства. Решением уравнения служат точки прямой которые можно получить в результате последовательного обнуления одной из переменных:

1. 

Построим прямую . Она проходит через точки (0;6) и (6;0). На рисунке обозначим (1). Для того чтобы определить, какая плоскость удовлетворяет неравенству, необходимо выбрать любую точку не принадлежащую прямой. Выберем точку начала координат (0;0), подставим в неравенство и получим 0 ≤ 12. Данное утверждение является верным, следовательно, неравенству соответствует нижняя полуплоскость.

Аналогичным образом найдем области решения трех других неравенств:

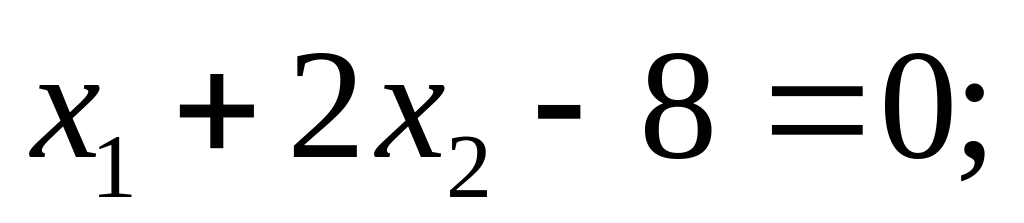
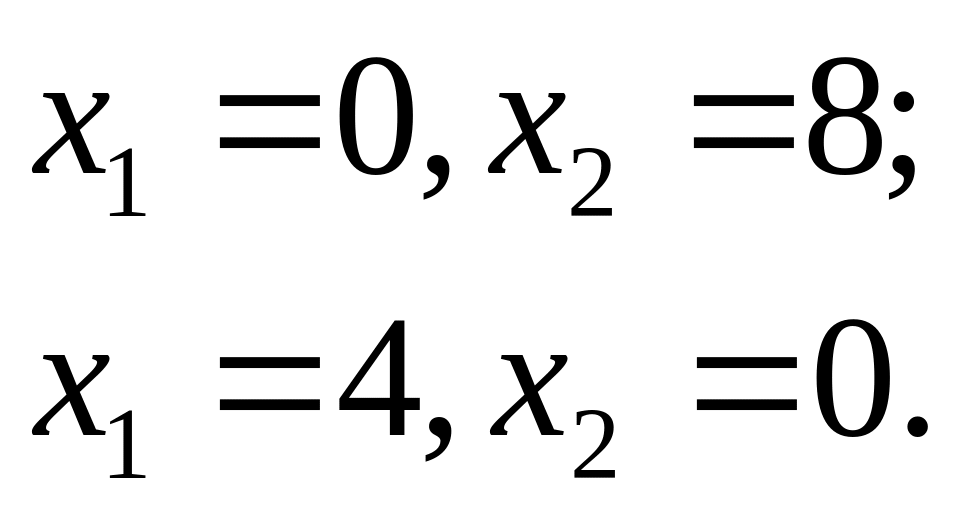2. (2)

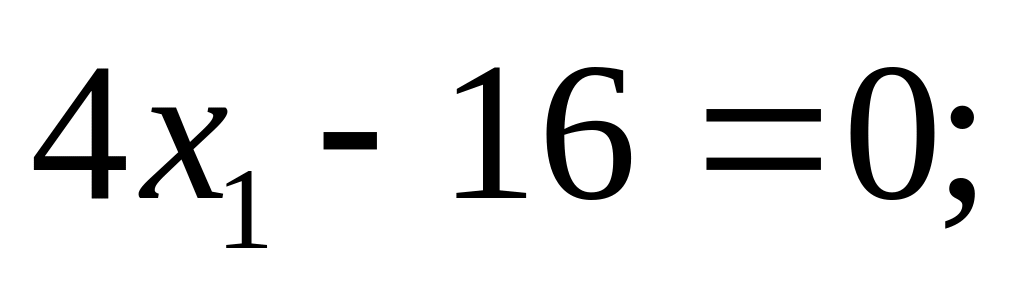
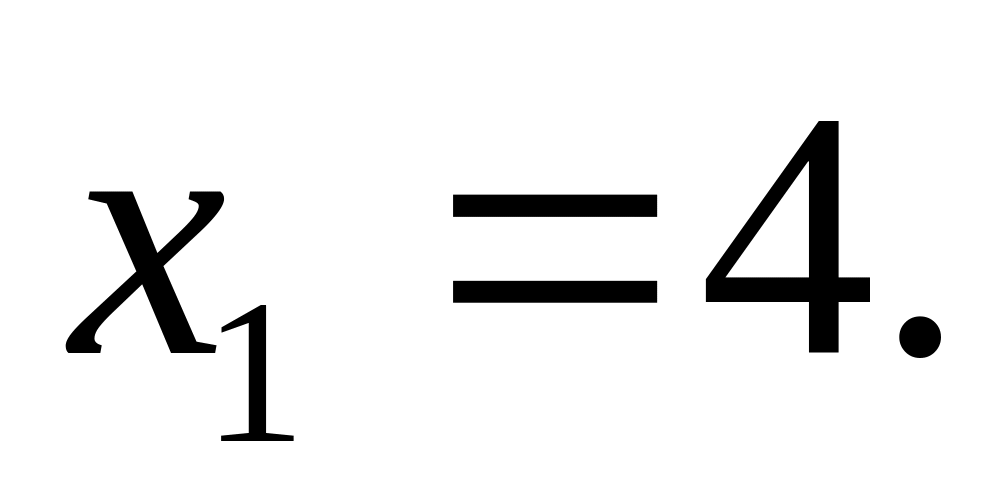3. (3)

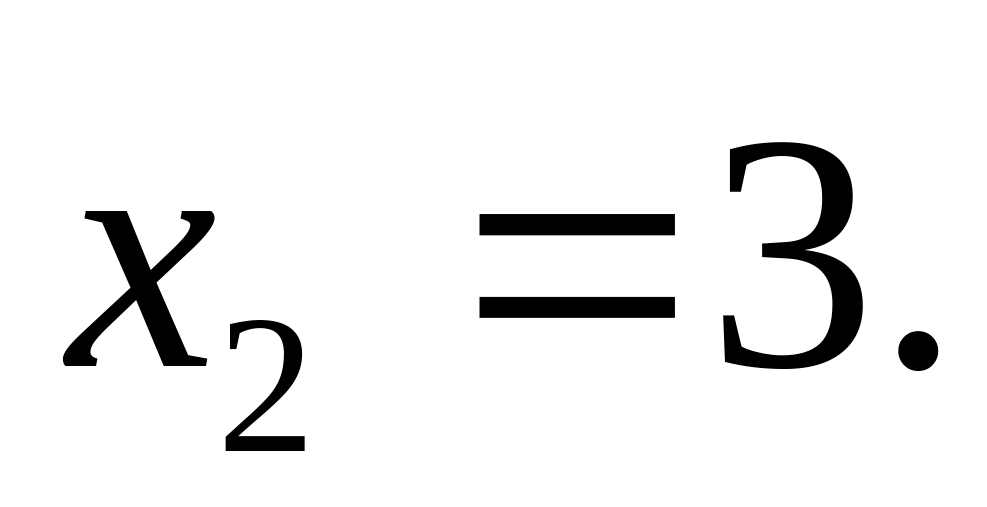4. (4)

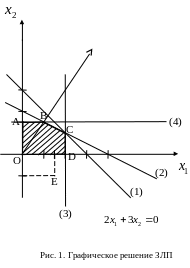
Пересечение этих нижних полуплоскостей, каждая из которых определяется соответствующим неравенством системы и удовлетворяет условиям неотрицательности, определяет многоугольник OABCD. Координаты любой точки, принадлежащей области определения, являются допустимым решением задачи. (Рис 1)

Приравниваем целевую функцию постоянной величине а:

а.

Пусть а = 0, вычислим координаты двух точек, удовлетворяющих соответствующему уравнению В качестве одной из точек удобно взять т.О (0;0), а если то в качестве второй точки возьмем т.E (3;–2). Через эти две точки проведем линию уровня .

Для нахождения максимального значения целевой функции при графическом решении задачи линейного программирования построим вектор-градиент, координаты которого являются частными производными целевой функции :

.

Перемещая линию уровня в направлении этого вектора до тех пор, пока она не покинет пределов области допустимых решений. Предельная точка области при этом движении и является точкой максимума C. Для нахождения координат этой точки достаточно решить два уравнения прямых, получаемых из соответствующих ограничений и дающих в пересечении точку максимума.

(4;2) - оптимальный план.

Значение целевой функции в этой точке равно:

max

Вывод:

Прибыль предприятия будет максимальной и составит 14 ден.ед., если продукция первого вида будет выпускаться в количестве 4-х изделий, а продукции второго вида в количестве 2-х изделий.

Если решать задачу на минимум, то необходимо найти такое решение, при котором предприятие получит наименьшую функцию. Минимум функции необходимо искать в точке области допустимых решений самой близкой к прямой при тех же ограничениях. Для этого нужно линию уровня смещать параллельно самой себе в направлении, противоположному вектору-градиенту Очевидно, что он достигается в т.О (0;0). Т.е. min , при

Тогда полученная прибыль будет равна 0. Значит, для того, чтобы получить минимально возможную прибыль (в данном случае вообще не получить ее) необходимо не производить продукцию.

ЗАДАЧА 2

Использовать аппарат теории двойственности для экономико-математического анализа оптимального плана задачи линейного программирования

Для изготовления четырех видов продукции используют три вида сырья. Запасы сырья, нормы его расхода и цены реализации единицы каждого вида продукции приведены в таблице.

Тип сырья	Нормы расхода сырья на одно изделие				Запасы сырья
	А	Б	В	Г
I	2	1	0,5	4	2400
II	1	5	3	0	1200
III	3	0	6	1	3000
Цена изделия	7,5	3	6	12

Требуется:

1. Сформулировать прямую оптимизационную задачу на максимум выручки от реализации готовой продукции, получить оптимальный план выпуска продукции.

2. Сформулировать двойственную задачу и найти ее оптимальный план с помощью теорем двойственности.

3. Пояснить нулевые значения переменных в оптимальном плане.

4. На основе свойств двойственных оценок и теорем двойственности:

• проанализировать использование ресурсов в оптимальном плане исходной задачи;

• определить, как изменятся выручка и план выпуска продукции при увеличении запасов сырья I вида на 100 единиц и уменьшении на 150 единиц запасов сырья II вида;

• оценить целесообразность включения в план изделия Д ценой 10 денежных единиц, если нормы затрат сырья 2, 4 и 3 единицы.

Решение:

1. Обозначим количество выпускаемых видов продукции А, Б, В и Г, соответственно как х₁, х₂, х₃, х₄. Число ограничений задачи равно числу ресурсов, используемых для изготовления изделий – 3. Дополнительно вводим условие неотрицательности переменных. Зная цены изделий, нормы их расхода и запасы ресурсов, формулируем математическую модель исходной задачи линейного программирования:

	A	B	C	D	E	F	G	H
1		Переменные
2		x1	x2	x3	x4	ЦФ
3		0	0	0	0
4	Коэффициент ЦФ	7,5	3	6	12	=СУММПРОИЗВ(B3:E3;B4:E4)
5
6	Ограничения					Левая часть		Правая часть
7	I	2	1	0,5	4	=СУММПРОИЗВ(B3:E3;B7:E7)	<=	2400
8	II	1	5	3	0	=СУММПРОИЗВ(B3:E3;B8:E8)	<=	1200
9	III	3	0	6	1	=СУММПРОИЗВ(B3:E3;B9:E9)	<=	3000

Оптимальный план выпуска продукции будем искать с помощью настройки «Поиск решения» табличного процессора Excel (меню «Сервис»). Создадим форму для ввода условий задачи:

П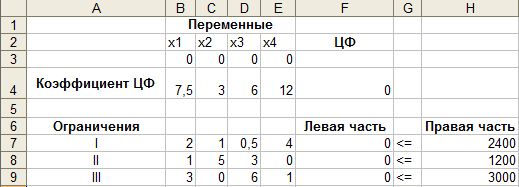 олучим:

Таблица 1

Теперь будем искать оптимальное решение с помощью настройки «Поиск решения». Введем ограничения:

Введём параметры поиска решения в диалоговом окне «Параметры поиска решения». Отметим пункты «Линейная модель» и «Неотрицательные значения»:

В результате будет получена следующая таблица:

Вывод:

Таким образом, для получения максимальной выручки следует выпускать 0 изделий вида А и Б (x₁= 0 и x₂= 0), 400 изделий вида В и 550 изделий вида Г. Выручка при этом будет составлять 9000 единиц.