Векторы, операции над ними.

Рассмотреть самостоятельно следующие понятия: вектор, длина вектора, нулевой и единичный вектор, равные вектора, коллинеарные и компланарные вектора, сложение и вычитание вектора по правилам треугольника и параллелограмма, умножение вектора на число.

Пусть задана ось L и некоторый вектор АВ. Проекцией вектора АВ на ось L называется величина А¢В¢ на оси L. Проекция вектора АВ на ось L равна длине вектора АВ, умноженной на косинус угла между вектором АВ и осью L, т.е.

Направляющими косинусами вектора `а называются косинусы углов между вектором `а и осями координат. Направляющие косинусы вектора `а можно определить по формулам

Векторы можно складывать, вычитать и умножать на число.

Определение 1. Суммой называется вектор, который идет из начала вектора в конец вектора при условий, что вектор приложен к концу вектора .

Определение 2. Разностью векторов и называется вектор, который в сумме с вектором дает вектор .

Определение 3. Произведением называется вектор, который коллинеарен вектору , имеет длину, равную и направление такое же, как и вектор , если >0 и противоположное, если <0.

Пусть даны векторы и . Тогда сумма векторов в координатной форме записывается

,

разность векторов

,

умножение вектора на число l

.

Определение 4. Скалярным произведением двух ненулевых векторов и называется число, равное произведению длин этих векторов на косинус угла между ними

Если векторы и заданы координатами, то скалярное произведение можно вычислить по формуле

Свойства скалярного произведения векторов:

.

.

.

.

. , если

Следствие. Угол между векторами и определяется по формуле

или

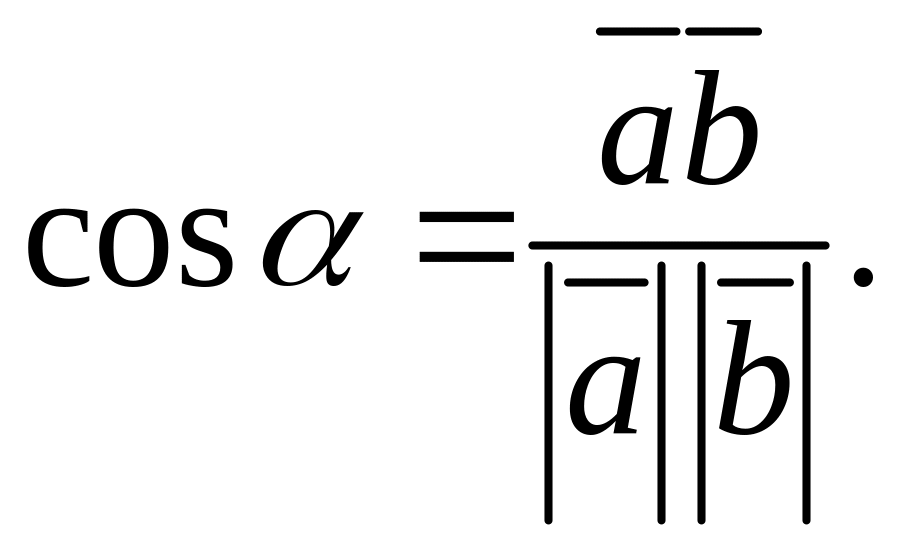
Сформируем условия параллельности перпендикулярности двух векторов и

1. Векторы и перпендикулярны, если их скалярное произведение равно 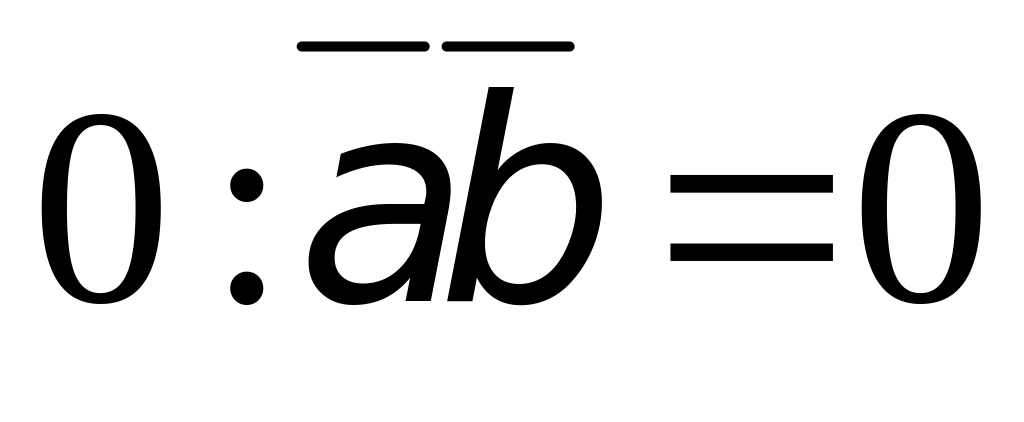, то есть

или

2. Векторы и параллельны, если их соответствующие координаты пропорциональны

Определение 5. Векторным произведением вектора на вектор называется вектор c, который:

1. перпендикулярен векторам и ;

2. имеет длину , - угол между векторами и ;

3. с конца вектора кратчайший поворот от вектора к вектору виден совершающимся против часовой стрелки.

Обозначается

Геометрический смысл векторного произведения: в результате векторного произведения получается вектор, длина которого численно равна площади параллелограмма, построенного на векторах и как на сторонах.

Свойства векторного произведения:

1. ;

2. ;

3. ;

4. .

Если , тогда .

Смешанное произведение векторов

Смешанным произведением векторов и называется произведение, составленное следующим образом: и обозначается .

Геометрический смысл смешанного произведения: в результате смешанного произведения получается число, равное объему параллелепипеда, построенного на векторах и как на ребрах

Свойства смешанного произведения:

1. ;

2.

3. вектора и компланарны.

Если , тогда .

Лекции 13-16.