Тема 5: Дифференциальное исчисление функции одной переменной.
1. Используя
определение производной, найти производную
функции
.
Решение.
Придавая аргументу х приращение
,
найдем соответствующее приращение
функции:
1.
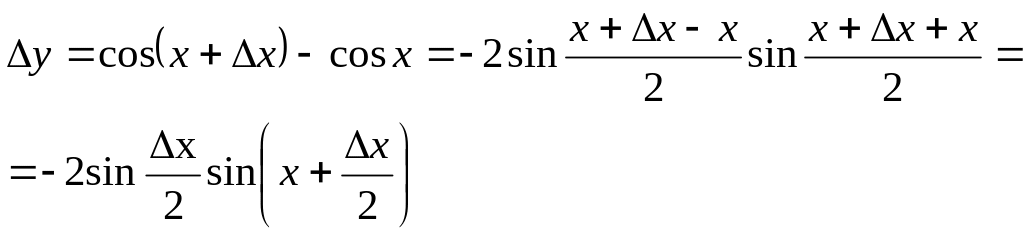
Найдем отношение:
Найдем предел этого отношения при
:
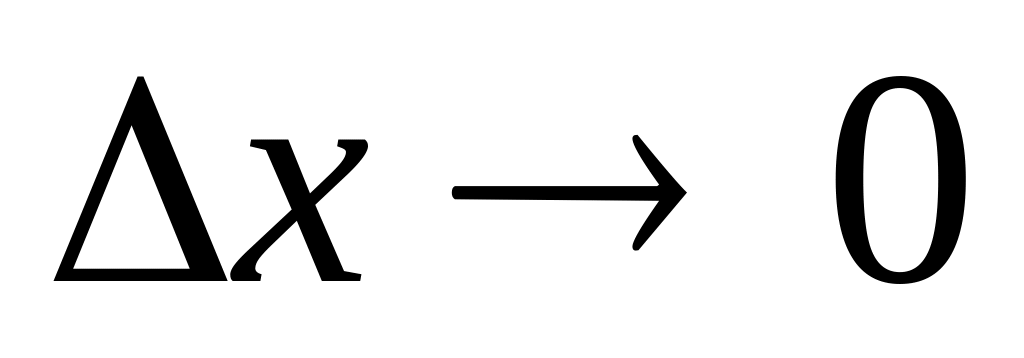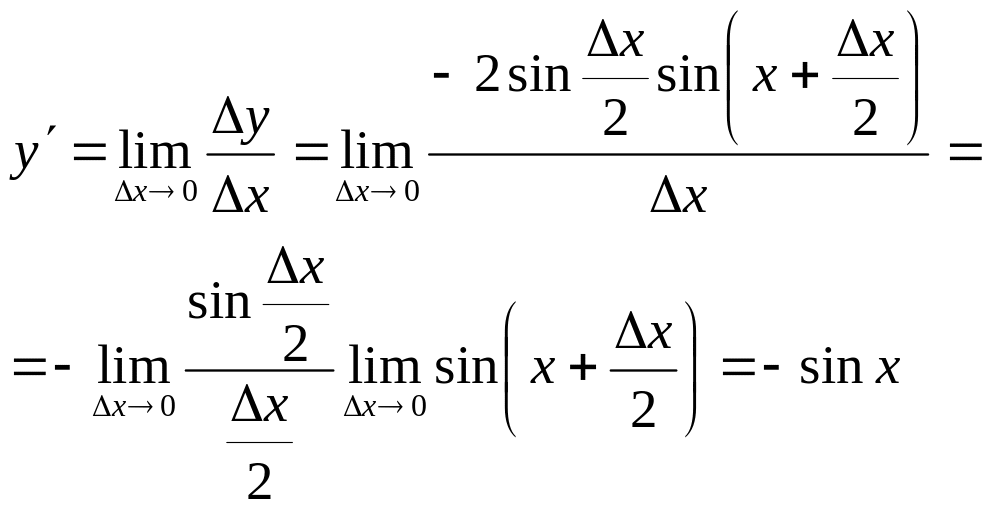
Таким образом:
.
2. Найти производные функций:
а)
;
б)
Решение. а) Используя правила дифференцирования (7.4), (7.6) и (7.8) формулы (7.14), (7.17) и (7.23), получим:
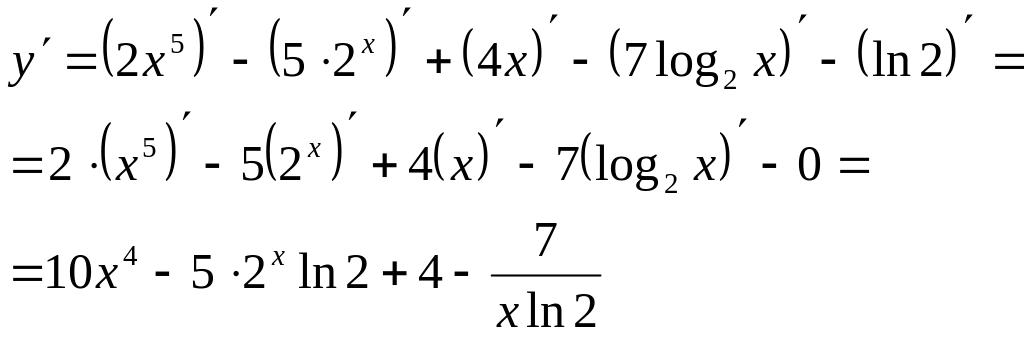
б) Используя правила дифференцирования сложной функции (7.12) и формулы (7.14), и (7.23), получим:
3.
Найти
производную функции:
Решение. Имеем показательно-степенную функцию. Используя метод логарифмического дифференцирования (7.13), получим:
Отсюда
имеем:
4.
Составить
уравнение касательной к графику функции
,
проходящую через точку
.
Решение.
Определим
абсциссу точки касания из условия, что
точка М
принадлежит
касательной, т.е. ее координаты
удовлетворяют уравнению
,
следовательно:
Подставляя
в это соотношение выражение для значения
функции и ее производной в точке
,
получим уравнение вида:
.
Решая его относительно
,
найдем, что
.
Определив значение функции и ее
производной в этой точке, уравнение
касательной запишем в виде:
,
или
.
5.
Используя
правило Лопиталя найти
.
Решение.
Так как в
данном случае имеется неопределенность
вида
,
можно применить правило Лопиталя:
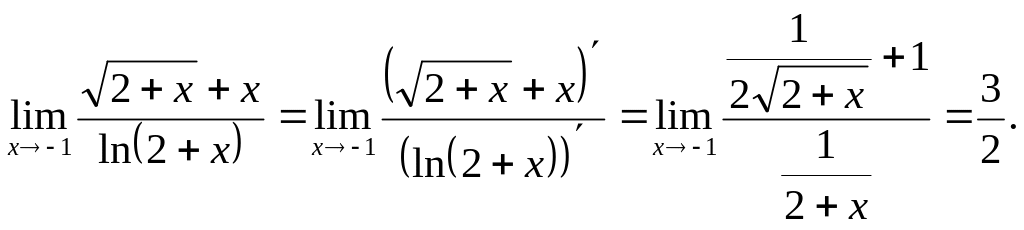
6.
Исследовать функцию
и построить ее график.
Решение:
1.
Область определения:
.
Точки х=-1
и х
=
1 — точки разрыва функции.
2.
,
т.е.
функция нечетная; ее график симметричен
относительно начала координат и
достаточно провести исследование
функции на интервале
.
3.
Прямые х = 1 и (в силу симметрии графика) х = -1 — вертикальные асимптоты.
4.
.
Прямая у
= 0
(ось
абсцисс) — двусторонняя горизонтальная
асимптота.
5.
при всех допустимых значениях х.
Экстремумов
нет, функция возрастает на интервалах
.
6.
при х
= 0.
Знаки второй производной
показаны
на рис. 1.
Рис. 1.
Функция
выпукла вниз на интервалах
и выпукла вверх на интервалах
.
Хотя
меняет свой знак при переходе через три
точки х=-1,
х=0, х=1,
но график функции имеет только одну
точку перегиба х=0,
ибо
в двух других точках х
= -1,
х
= 1
функция не определена.
7. Точка пересечения графика с осями единственная - начало координат (0; 0). График функции показан на рис. 2.
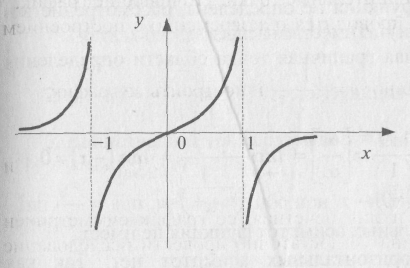
Рис.2.
7. Найти
дифференциал функции
в точке
двумя способами: а) выделяя линейную
относительно
часть приращения функции
;
б) по формуле
.
Решение:
а) Приращение функции
.
Выделяя линейную относительно
часть приращения функции, получим:
.
б) Дифференциал функции
.
8. Найти
.
Решение:
Получим вначале приближённую формулу для вычисления любой -ой степени.
Полагая
,
найдём:
и в соответствии с формулой (8.5):
.
В данном е для
:
;
9. Найти
и
,
если
.
Решение:
;
.
Тема 6: Дифференциальное исчисление функции многих переменных
Тема 7: Интегральное исчисление.
Найти неопределённые интегралы:
а)
;
б)
.
Решение:
а) Вынося постоянный множитель
за знак интеграла, приходим к табличному
интегралу:
б) Используя свойства интегралов, приходим к сумме табличных интегралов:
.
2. С помощью метода замены вычислить интегралы:
а)
;
б)
;
Решение:
а)
.
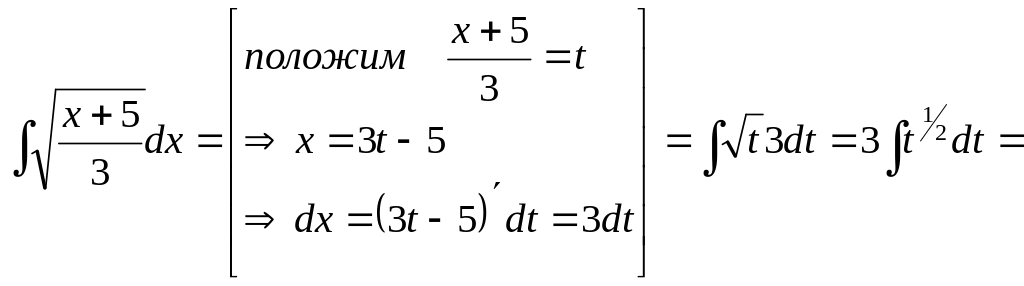
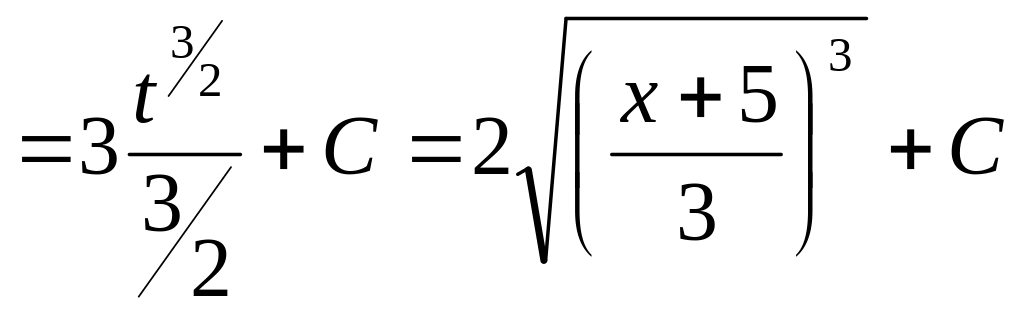В простых примерах новую переменную часто не выписывают явно. В этих случаях говорят о преобразовании функции под знаком дифференциала или о введении постоянных и переменных под знак дифференциала. При этом следует учитывать, что, например,
,
где
и
- некоторые числа (
).
б) Заметим, что
,
а
.
Тогда
3. Используя формулу интегрирования по частям, вычислить интегралы:
а)
;
б)
.
а) Положим
и
.
Тогда
и
.
Согласно формуле интегрирования по
частям:
.
б)
.
4. Методом неопределённых коэффициентов вычислить интегралы:
.
Решение:
Записывая подынтегральную функцию в
виде суммы простейших дробей с
неопределёнными коэффициентами
,
имеем:
После приведения выражения правой части к общему знаменателю:
.
Полученное равенство выполняется тождественно при равенстве числителей:
Сравнивая коэффициенты при равных
степенях
,
получим:
.
Найденные значения подставим в сумму простейших интегралов:
.
5. Используя тригонометрические формулы, вычислить интегралы:
а)
;
б)
.
Решение:
а) Так как
и приняв
,
получим:
.
б) Используя формулу двойного угла, а затем тригонометрическую формулу понижения степени, получим:
