Тема 4: Функция. Предел функции.

1. Найти область определения функции

Решение: Так как выражение под корнем четной степени должно быть неотрицательно, знаменатель дроби отличен от нуля, а выражение, стоящее под знаком логарифма, должно быть положительно, то область определения функции найдем из системы неравенств:

или

откуда

Значения переменной х, которые удовлетворяют всем неравенствам системы одновременно, есть .

2. Найти область значений функции

Решение: Воспользуемся определением обратной функции, в соответствии с которым область ее определения будет являться областью значений исходной функции. Найдем функцию, обратную к функции , выражая х через у: . Так как то . Так как то , откуда , т.е. найденный полуинтервал и является областью значений искомой функции.

3. Выяснить четность (нечетность) функции

Решение: Найдем

.

Так как , то по определению искомая функция является четной.

4. Найти основной (наименьший) период функции .

Решение. По определению периодической функции , для любых х и . Для имеем:

, откуда Полученное равенство будет выполняться при любых х, т.е. тождественно, если сомножитель, не содержащий х, будет равен нулю, т.е. и наименьшее (не равное нулю) .

5. Найти

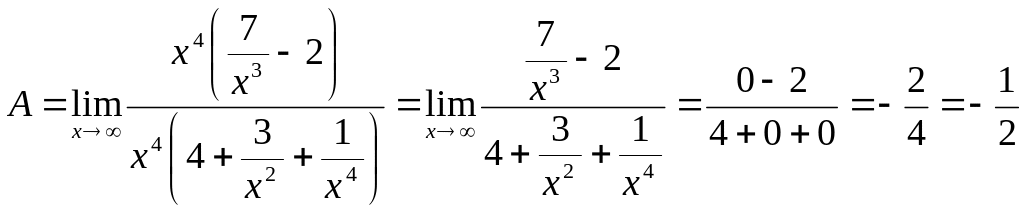Решение. . Вынося за скобку и в числителе и в знаменателе х в наибольшей степени, получим так как - величины бесконечно малые при .

6. Найти

Решение. . Чтобы выяснить, какова наибольшая степень среди слагаемых дроби, следует сначала вынести х с наибольшим показателем степени в выражениях под знаком радикала:

.

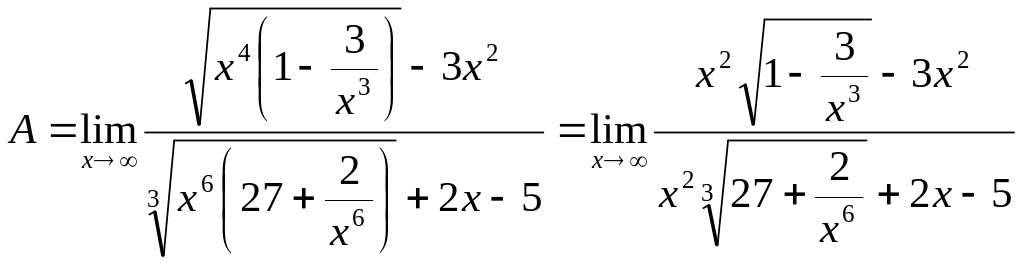Наибольшая степень вторая; вынося за скобку , получим

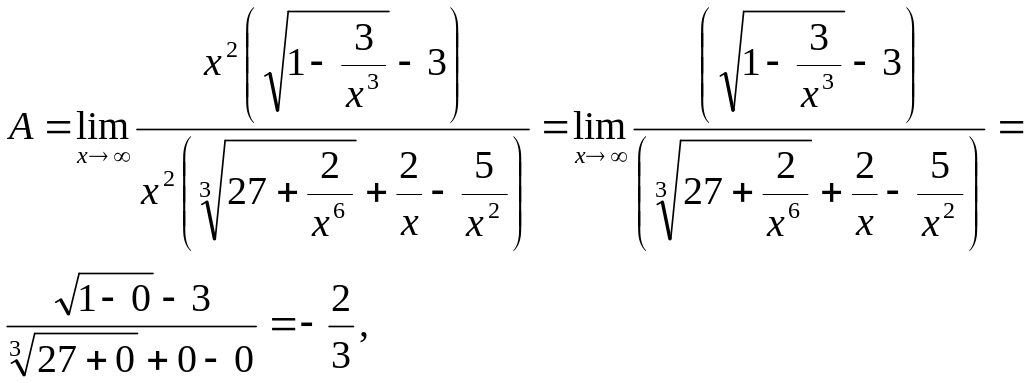
так как - бесконечно малые величины при .

7. Найти .

Решение. Имеем неопределенность вида . Приведем дроби к общему знаменателю:

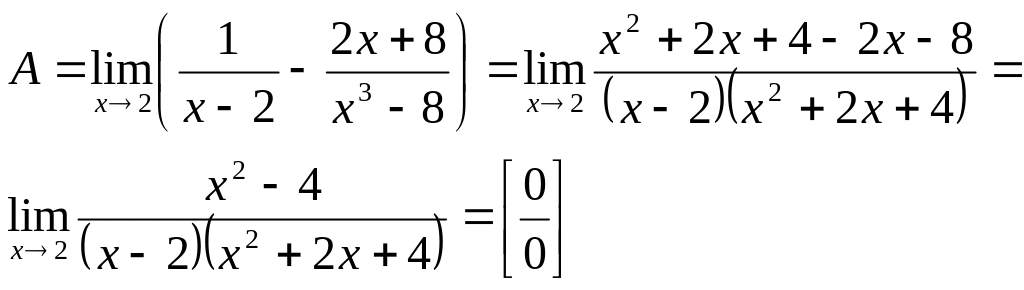
Имеем предел 2-го типа, необходимо разложить на множители числитель дроби. Получим

8. Найти .

Решение. Имеем неопределенность вида . Домножим и разделим функцию, стоящую под знаком предела на сопряженное выражение, приводящее к разности квадратов:

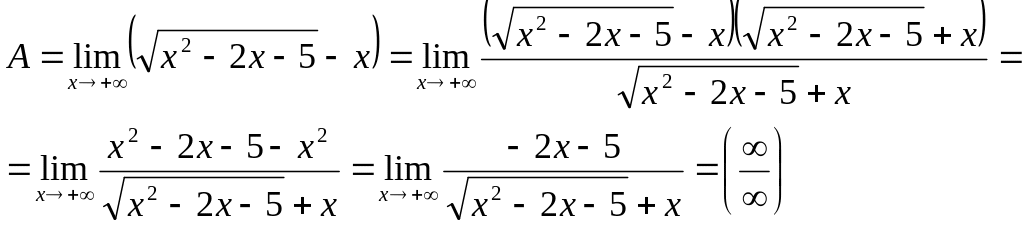Имеем предел 1-го типа. Решая далее найдем

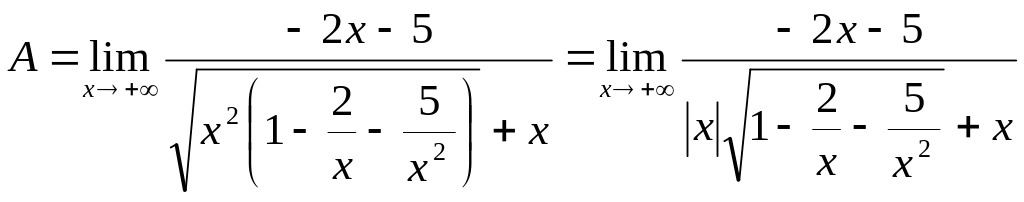
При по определению модуля; поэтому

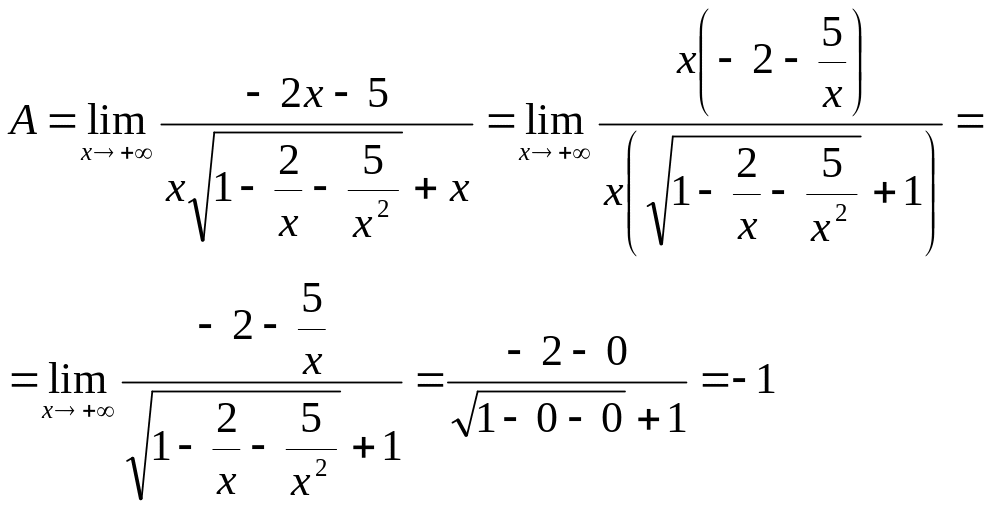
так как при - бесконечно малые величины.

9. Найти .

Решение. Имеем неопределенность вида , так как .

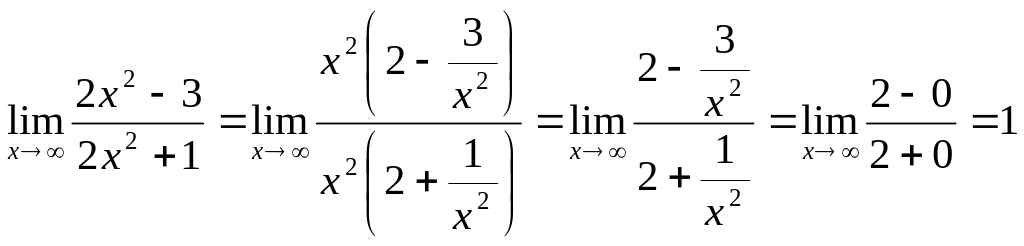Выделим целую часть дроби

является бесконечно малой величиной при . Домножим показатель степени на , это действие не нарушает знака равенства:

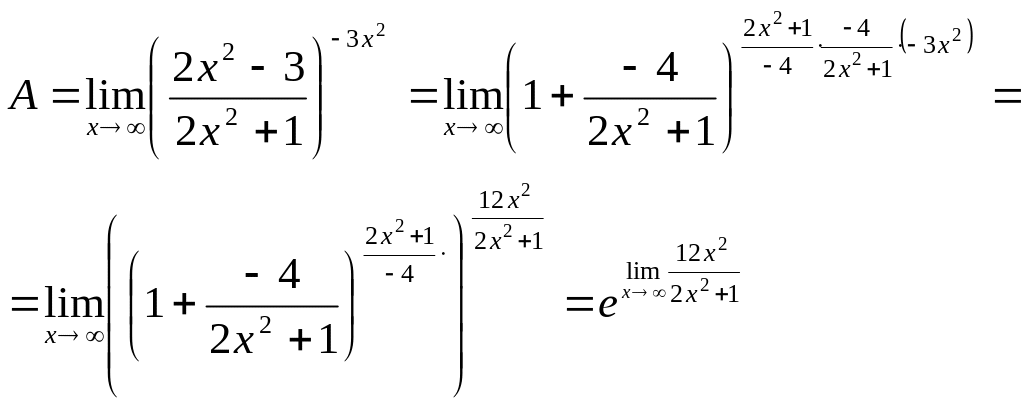
ибо . Найдем . Имеем неопределенность вида , предел 1-го типа. Вынесем за скобки , так как вторая степень наибольшая:

,

так как . Таким образом, искомый предел равен .

10. Найти .

Решение. .

Первый сомножитель представляет собой первый замечательный предел и равен 1, второй сомножитель представляет предел, равный . Таким образом, искомый предел равен 1.

11. Найти .

Решение. . Сделаем преобразования, приводящие ко второму замечательному пределу:

.

Выражение в квадратных скобках представляет второй замечательный предел: , следовательно, .

Найдем предел показателя степени:

Таким образом, .

12. Исследовать на непрерывность функции в точке . В случае разрыва установить его характер в точке :

а) ; б) .

Решение:

а) При функция не определена, следовательно, функция в точке терпит разрыв:

т.е. конечный предел существует; следовательно, - точка устранимого разрыва первого рода. (Доопределив функцию в точке , т.е. положив получим, что новая функция

будет уже непрерывна в точке .)

б) При функция не определена, следовательно, функция в точке терпит разрыв: .

Так как односторонние пределы (достаточно было бы одного) бесконечны, то - точка разрыва функции второго рода.