Тема 1: Элементы линейной алгебры.
1. Найти
матрицу
,
где
,
.
Решение:
Найдём матрицу
,
транспонированную к
,
т.е. меняем строки и столбцы местами:
.
Найдём матрицу
,
умножив все элементы матрицы
на 3. Произведём вычитание матриц
и
(поэлементно):
2. Найти произведение матриц и , если
,
Решение:
Произведение
матриц
не
существует; поэтому найдём произведение
.
Выделим элементы матрицы
;
- это сумма произведений элементов 1-ой
строки первой матрицы
на элементы 1-го столбца второй матрицы
:
;
аналогично
;
.
Точно также
находятся элементы 2-ой строки матрицы
:
;
;
.
Таким образом,
.
3. Вычислить определители матрицы :
а)
;
б)
Решение:
а) По формуле (1.7)
;
б) по формуле
(1.8)
.
4. Вычислить тот же определитель, приведённый в задаче 3(б), используя его разложение по элементам: первой строки.
Решение:
Находим алгебраические дополнения элементов первой строки по формуле (1.9):
;
;
.
Теперь по теореме Лапласа (1.10):
5. Выяснить, является ли матрица
обратной к матрице
.
Решение:
Найдём
произведения
и
:
;
.
Матрицы и являются взаимно обратными.
6. Найти матрицу, обратную к данной:
.
Решение:
Находим определитель матрицы
.
Так как
,
то матрица
- вырожденная и обратная матрица
существует и единственна.
Транспонируем матрицу:
.
Находим алгебраические дополнения
всех элементов транспонированной
матрицы
и составляем из них присоединённую
матрицу
:
;
;
;
;
;
;
;
;
,
т.е.
.
Находим обратную матрицу по формуле (1.11):
.
Проверяем правильность вычисления обратной матрицы по формуле (1.6):
,
где
- единичная матрица 3-го порядка.
7. Решить систему уравнений методом Крамера:
.
Решение:
Определитель
,
следовательно, по методу Крамера система
имеет единственное решение. Вычислим
определители матриц
,
полученных из матрицы
заменой соответственно первого, второго,
и третьего столбцов столбцом свободных
членов:
,
,
.
Теперь по формулам Крамера (1.15):
,
,
.
Ответ: (1;0;-2).
8. Методом обратной матрицы решить систему уравнений:
.
Решение:
Обозначим:
;
;
.
Тогда в матричной
форме система имеет вид:
.
Определитель матрицы
,
т.е. обратная матрица существует:
.
Теперь по формуле (1.14):
.
Ответ: (3;2;1).
Тема 2: Элементы векторной алгебры.
1. Даны
четыре вектора:
,
,
,
.
Необходимо: а) разложить вектор
по векторам
,
,
;
б) найти длину и направление вектора
Решение:
а) По
условию
,
где
,
,
- некоторые числа. Следовательно,
.
Приравнивая
коэффициенты при единичных векторах
(ортах)
,
получим систему:
,
откуда следует
,
т.е.
.
б) Найдём
вектор
:
.
Его длина
,
а направляющие косинусы найдём по
формулам (2.4):
.
2. Даны
два единичных вектора
и
,
угол между которыми
.
Найти: а) острый угол между диагоналями
параллелограмма, построенного на
векторах
и
;
б) проекцию вектора
на направление вектора
.
Решение.
а) Искомый угол (рис 1.)определим по формуле (2.13):
.
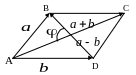
Рис 1.
где 
,
.
Найдём скалярное произведение векторов
и
и их длины:
;
;
.
Теперь
и
.
б) По формуле (2.8):
.
Найдём
;
.
Теперь
.