33. Преобразование Лапласа. Связь с преобразованием Фурье

Прямое преобразование Лапласа

Преобразованием Лапласа функции вещественной переменной  , называется функция   комплексной переменной  ^[1], такая что:

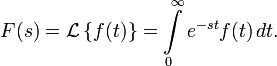
Правая часть этого выражения называется интегралом Лапласа.

[править]Обратное преобразование Лапласа

Обратным преобразованием Лапласа функции комплексного переменного  , называется функция   вещественной переменной, такая что:

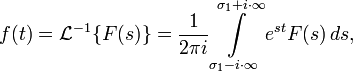
где   — некоторое вещественное число (см. условия существования). Правая часть этого выражения называется интегралом Бромвича.

[править]Двустороннее преобразование Лапласа

Основная статья: Двустороннее преобразование Лапласа

Двустороннее преобразование Лапласа — обобщение на случай задач, в которых для функции   участвуют значения  .

Двустороннее преобразование Лапласа определяется следующим образом:

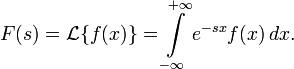
[править]Дискретное преобразование Лапласа

Применяется в сфере систем компьютерного управления. Дискретное преобразование Лапласа может быть применено для решётчатых функций.

Различают  -преобразование и  -преобразование.

• -преобразование

Пусть   — решётчатая функция, то есть значения этой функции определены только в дискретные моменты времени  , где   — целое число, а   — период дискретизации.

Тогда применяя преобразование Лапласа получим:

• -преобразование

Основная статья: Z-преобразование

Если применить следующую замену переменных:

получим  -преобразование:

Непрерывное преобразование Фурье эквивалентно двустороннему преобразованию Лапласа с комплексным аргументом  :

34. Основные теоремы об оригиналах и изображениях

35. Свертка оригиналов

Свертка оригиналов.

Сверткой оригиналов   и   называется функция

.

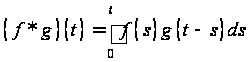Функции f (t) и g(t) называются компонентами свертки.

Найдем для примера свертку произвольного оригинала   и единичной функции   Имеем  .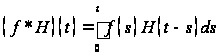

Так как   при   то

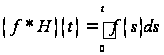. (2.1.1)

Теорема 1. Если   и , то

.

∆

Действительно, по определению интеграла Лапласа имеем

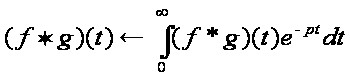
Воспользуемся определением свертки:

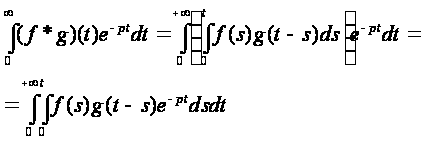
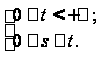
Изменив порядок интегрирования в двойном интеграле, получим

.

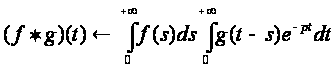Введем вместо t новую переменную  . Тогда

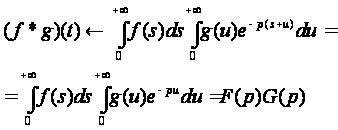
что и требовалось доказать. ▲

Свойство линейности.

Для любых комплексных постоянных и :

∆

Это свойство вытекает из свойства линейности интеграла.

Домножим равенство 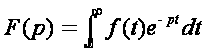  на α: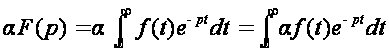 

Так как  , то  , то есть

36. Применение операционного исчисления

Свертка оригиналов. 8 2.1 Свойство линейности. 9 2.2 Теорема подобия. 9 2.3 Теорема запаздывания. 10 2.4 Теорема смещения. 10 2.5 Теорема упреждения. 11 2.6 Умножение оригиналов. 11 2.7 Дифференцирование оригинала. 11 2.8 Дифференцирование изображения. 12 2.9 Интегрирование оригинала. 12 2.10 Интегрирование изображения. 13 §3. Изображения простейших функций. 13 §4. Отыскание оригинала по изображению.. 15 4.1 Разложение на простейшие дроби. 15

37. Вычисление оригиналов по известному изображению

Найти оригинал f(t) по его операторному изображению F(s) можно в общем случае по формуле обратного преобразования Лапласа

.

Однако при расчете переходных процессов это выражение крайне редко используют непосредственно. Если изображение F(s) представляет однозначную функцию переменной s, и выполняется условие  , то путь интегрирования в последнем интеграле можно считать замкнутым (штриховая линия на рис. 19.1) и воспользоваться для вычисления интеграла по замкнутому контуру теоремой о вычетах. Тогда

,

где s_k — особые точки функции F(s), охваченные контуром интегрирования.

Обычно при расчете переходных процессов в цепях с сосредоточенными параметрами изображения F(s) представляют собой дробно-рациональные функции с простыми полюсами и конечным пределом  . Очевидно, это имеет место для правильной рациональной дроби  . При выполнении указанного условия и отсутствии кратных полюсовF(s) использование правила вычисления вычетов в простых полюсах приводит к выражению для оригинала

,

где s_k — корни знаменателя H(s) = 0; H '(s) = dH/ds; суммирование идет по всем полюсам.

Последняя формула называется также теоремой разложения. Примеры ее применения к нахождению оригиналов даны в Задачe 15.1 и Задачe 15.2

Если рациональная дробь F(s) имеет целую часть, что свидетельствует о том, что оригинал неограничен при t  0, то необходимо выделить эту целую часть. Ей отвечает оригинал в виде -импульса  . Остаток F(s) представляет собой правильную дробь, к которой применяют теорему разложения. Соответствующий пример рассмотрен в Задачe 15.2

Присутствие в операторном изображении сомножителей вида e^s свидетельствует о наличии в решении слагаемых, запаздывающих на время  от начала исходного процесса при t = 0. Алгебраические сомножители в таких слагаемых приводятся к оригиналу с помощью теоремы разложения, а при суммировании учитывается их сдвиг на время . Например, при вычислении оригинала функции F(s) = [s +  (1 – e^s)]/[s(s + )]  рассмотрим сначала отдельно слагаемое F₁(s) = (s +  )/[s(s + )] = 1/s.. Как известно из сводки основных формул (Приложениe 4), ему отвечает оригинал в виде единичной функции. Второе слагаемое F₂(s) = [–s +  )]e^s  имеет алгебраический сомножитель –s +  ), для которого с помощью теоремы разложения найдем  . Так как t' = t – , то окончательно запишем  . Соответствующая зависимость изображена на рис. 19.6.

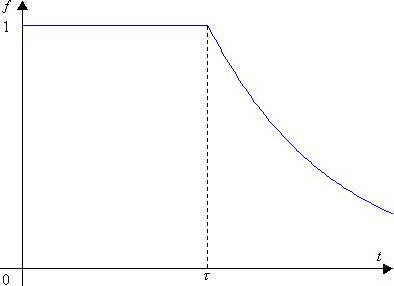
Рис. 19.6

Рассмотренные способы определения оригинала принципиально ограничены однозначными функциями F(s). Если изображение представляет собой многозначную функцию комплексной переменной s, имеющую точки разветвления, для нахождения оригинала  следует использовать общую интегральную формулу обратного преобразования Лапласа. В теории цепей такие задачи возникают при рассмотрении цепей с распределенными параметрами или их моделей с бесконечным количеством сосредоточенных элементов, когда изображения содержат переменную s под знаком корня (например, при рассмотрении процессов в бесконечно длинных кабелях.