Формулировка

Пусть   — область на комплексной плоскости с кусочно-гладкой границей  , функция   — голоморфна в   и   — точка внутри области  . Тогда справедлива следующая формула Коши:

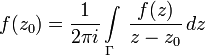
Формула справедлива также, если предполагать, что   голоморфна внутри  , и непрерывна на замыкании, а также если граница   не кусочно-гладкая, а всего лишьспрямляемая.

[Править]Доказательство

Рассмотрим окружность   достаточно малого радиуса   с центром в точке  . В области, ограниченной контурами   и   подынтегральная функция не имеет особенностей и по интегральной теореме Коши интеграл от неё по границе этой области равен нулю. Это означает, что не зависимо от   имеем равенство:

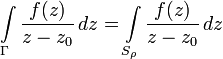
Для расчёта интегралов по   применим параметризацию  . Сначала докажем формулу Коши отдельно для случая  :

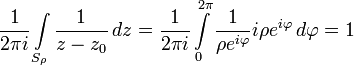
Воспользуемся ею для доказательства общего случая:

Так как функция   комплексно дифференцируема в точке  , то:

Интеграл от   равен нулю:

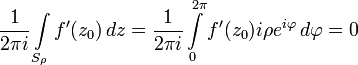
Интеграл от члена   может быть сделан сколь угодно мал при  . Но поскольку он от   вообще не зависит, значит он равен нулю. В итоге получаем, что

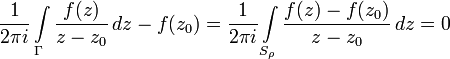
30. Ряд Лорана

Ряд Лорана — двусторонне бесконечный степенной ряд по целым степеням  , то есть ряд вида

Этот ряд понимается как сумма двух рядов:

1.  — положительная часть ряда Лорана (иногда называется правильной) и

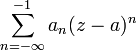2.  — отрицательная часть ряда Лорана (иногда называется главной).

При этом ряд Лорана считается сходящимся тогда и только тогда, когда сходятся его правильная и главная части. Термин назван в честь французского математикаП. А. Лорана.

[Править]Свойства

• Если внутренность области сходимости ряда Лорана непуста, то она представляет собой круговое кольцо

• Во всех точках своего кольца сходимости   ряд Лорана сходится абсолютно;

• Как и для степенных рядов, поведение ряда Лорана в точках граничных окружностей кольца сходимости может быть самым разнообразным;

• На любом компактном подмножестве 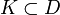  ряд сходится равномерно;

• Сумма ряда Лорана в   есть аналитическая функция  ;

• Ряд Лорана можно дифференцировать и интегрировать в   почленно;

• Разложение в ряд Лорана единственно, то есть если суммы двух рядов Лорана совпадают в  , то совпадают и все коэффициенты этих рядов.

• Коэффициенты 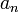  ряда Лорана определяются через его сумму   формулами

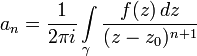
где  ,  ,   — любая окружность с центром a, расположенная внутри кольца сходимости.

31. Изолированные особые точки

Изолированная особая точка — точка, в некоторой проколотой окрестности которой функция   однозначна и аналитична, а в самой точке либо не задана, либо недифференцируема.

[Править]Классификация

Если   — особая точка для  , то, будучи аналитической в некоторой проколотой окрестности этой точки разлагается в ряд Лорана, сходящийся в этой окрестности.

.

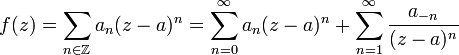Первая часть этого разложения называется правильной частью ряда Лорана, вторая - главной частью ряда Лорана.

Тип особой точки функции определяется по главной части этого разложения.

32. Вычеты и их применение

 Вычеты и их применение 

       - вычет функции f(z) относительно изолированной особой точки z₀:

(в круге   нет других особых точек).

     Если 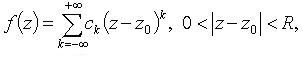  то

     Вычисление вычетов 

     1. z₀ - устранимая особая точка:

     2. z₀ - полюс:

     а) z₀ - простой полюс:

В частности, если   то

     б) z₀ - полюс порядка m:

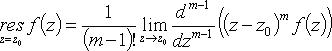
(формула также верна, если z₀ - полюс порядка не выше m).

     3. z₀ - существенно особая точка. Вычет находится по разложению в ряд Лорана.

Вычет относительно бесконечно удаленной точки 

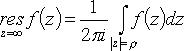
(f(z) - аналитическая в области   обход контура - по часовой стрелке).

c_-1 - коэффициент при z^-1 в разложении f(z) в ряд Лорана в окрестности точки  .

     Вычисление вычета в бесконечно удаленной точке 

     1.   - правильная точка:

 - нуль:

     В частности, если   при   то

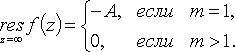
     2.   - полюс порядка не выше m:

     3. Если f(z) представима в ви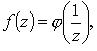де   где   - аналитическая в точке   то

     Если f(z) имеет конечное число особых точек z_k, k = 1, 2, ..., n, в конечной части плоскости, то

Основная теорема о вычетах 

     Если f(z) - аналитическая на границе   области D и внутри области, за исключением конечного числа особых точек z₁, z₂, ..., z_n, лежащих в D, то

(обход контура положительный).