1.Понятие двойного интеграла.

О бобщением определенного интеграла на случай функций двух переменных является так называемый двойной интеграл.

Пусть в замкнутой области D плоскости Оху задана непрерывная функция z=ƒ(х;у). Разобьем область D на n «элементарных областей» 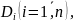 площади которых обозначим через ΔS_i, а диаметры (наибольшее расстояние между точками области) - через d_i(см. рис. 3).

В каждой области D_i выберем произвольную точку M_i(x_i;y_i), умножим значение ƒ(х_i;у_i) функции в этой точке на ΔS_i и составим сумму всех таких произведений:

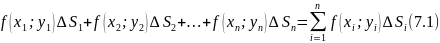
 Эта сумма называется интегральной суммой функции ƒ(х;у) в области D.

Рассмотрим предел интегральной суммы (7.1), когда n стремится к бесконечности таким образом, что max d_i → 0. Если этот предел существует и не зависит ни от способа разбиения области D на части, ни от выбора точек в них, то он называется двойным интегралом от функции ƒ(х;у) по области D и обозначается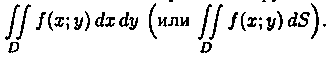

Таким образом, двойной интеграл определяется равенством

2 . Сведение двойного интеграла к повторному.

Пусть у₁(х), у₂(х) непрерывны на отрезке [a, b], у₁(х)≤ у₂(х) на всем отрезке.

D={x,y}: a≤x≤b; y₁(x) ≤y≤y₂(x)

Отрезок [a,b] – проекция D на ось ох. Для такой области любая прямая, параллельная OY и проходящая через внутреннюю точку области D пересекает границу области не более чем в 2 точках. Такая область наз. правильной в направлении оси OY.

Если функция f(x,y) задана на D и при каждом х Î [a,b] непрерывна на у , на

отрезке, [y₁(x),y₂(x)], то фц-ия

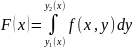
, наз. интегралом, зависящим от параметра I, а интеграл:

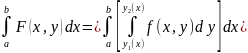
, наз повторным интегралом от ф-ции f(x,y) на области D. Итак, повторный

интеграл вычисляется путем последовательного вычисления обычных определенных

интегралов сначала по одной, а затем по другой переменной.

3.Замена переменных в двойном интеграле.

Для вычисления двойного интеграла иногда удобнее перейти в другую систему координат. Это может быть обусловлено формой области интегрирования или сложностью подынтегральной функции. В новой системе координат вычисление двойного интеграла значительно упрощается.

Замена переменных в двойном интеграле описывается формулой

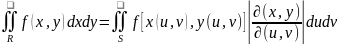
где выражение 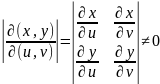представляет собой так называемый якобиан преобразования (x,y)→(u,v), а S − образ области интегрирования R, который можно найти с помощью подстановки x=x(u,v), y=y(u,v) в определение области R. Отметим, что в приведенной выше формуле означает абсолютное значение соответствующего определителя.

Предполагая, что преобразование координат (x,y)→(u,v) является взаимно-однозначным, обратное соотношение описывается якобианом

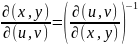при условии, что знаменатель нигде не равен 0.

Итак, замена переменных в двойном интеграле производится с помощью следующих трех шагов:

• Найти образ S в новой системе координат (u,v) для исходной области интегрирования R;

• Вычислить якобиан преобразования (x,y)→(u,v) и записать дифференциал в новых переменных ;

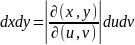• Заменить в подынтегральном выражении исходные переменные x и y, выполнив, соответственно, подстановки x=x(u,v) и y=y(u,v).