Числовые характеристики дискретных случайных величин

Числа, которые описывают случайную величину суммарно, называют числовыми характеристиками случайной величины. Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности: , где   – возможные значения случайной величины  , а   – соответствующие вероятности. Замечание. Вышеприведенная формула справедлива для дискретной случайной величины, число возможных значений которой конечно. Если же случайная величина имеет счетное число возможных значений, то для нахождения математического ожидания используют формулу: , причем это математическое ожидание существует при выполнении соответствующего условия сходимости числового ряда в правой части равенства. Вероятностный смысл математического ожидания: математическое ожидание приближенно равно (тем точнее, чем больше число испытаний) среднему арифметическому наблюдаемых значений случайной величины.

45. Непрерывная случайная величина

 Непрерывные случайные величины       Интегральная функция (функция распределения) 

     Свойства:

     1)  ;

     2)  ;

     3)  ;

     4)  .

     Дифференциальная функция распределения (плотность вероятности) 

где F(x) - интегральная функция.

     Свойства:

     1)  ;

     2)  ;

     3)  ;

     4)  .

     Числовые характеристики непрерывной случайной величины       Математическое ожидание 

     Дисперсия 

46. Основные распределения случайных величин

Некоторые законы распределения непрерывных случайных величин       Равномерное распределение 

     Нормальное распределение (распределение Гаусса) 

где   - функция Лапласа;

47. Предельные теоремы теории вероятностей

ЦПТ Ляпунова Александра Михайловича Если случайная величина 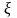представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то имеет распределение, близкое к нормальному

Теорема Муавра (локальная теорема Муавра – Лапласа) Вероятность того, что в независимых опытах событие наступит раз, если в каждом из опытов вероятность появления события постоянна и равна , приближённо выражается формулой:

, то есть приближённо является нормальным .

(доказана в 1730 г.)

Интегральная теорема Муавра – Лапласа Вероятность того, что в независимых опытах событие наступит не менее раз и не более , если в каждом из опытов вероятность появления события постоянна

и равна , приближённо выражается формулой:

,

где – функция Лапласа,

.

48. Многомерные случайные величины

Многомерная случайная величина — упорядоченный набор (вектор)   фиксированного числа   одномерных случайных величин. Многомерное наблюдение   — реализация м.с.в. Как правило  . Многомерная выборка   — неупорядоченный набор фиксированного числа   многомерных наблюдений. Основными числовыми характеристиками м.с.в. являются вектор средних и ковариационная матрица.

Корреляция и регрессия

Две случайные величины могут быть независимыми, либо быть связаны функциональной или статистической зависимостью. Статистической называют зависимость, при которой изменение одной величины влечёт изменение закона распределения другой.

Частным случаем статистической зависимости является корреляционная зависимость. В этом случае изменение одной величины влечёт за собой изменение математического ожидания другой (напр, рост-вес, образование-зарплата).

Корреляционную зависимость Y от X можно описать с помощью уравнения вида: , которое называется уравнением регрессии Y на X.

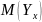- условное математическое ожидание величины Y, соответствующее данному значению x.

Обратную корреляционную зависимость (если она существует) можно описать уравнением регрессии X на Y:

Графики функций регрессии f(x) и ϕ(y) называются линиями регрессии. Различают линейные и нелинейные зависимости.

В случае линейной зависимости уравнения задаются в виде ; .

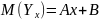При большом количестве X и Y математические ожидания заменяются на: ; .

Корреляционный анализ

Реально имеющуюся зависимость между случайными величинами оценивают по ограниченным выборкам путём расчёта выборочного коэффициента корреляции.

Определив его, с учётом достоверности можно дать ответ о наличии, направлении и силе.

Ковариация выборочных значений случайных величин X и Y:

Коэффициент корреляции:

– связь между величинами есть; – связи нет

– прямая связь; - обратная связь

– сильная связь

- умеренная связь

- слабая связь

Погрешность:

нулевая гипотеза отвергается

Р егрессионный анализ

Регрессия – это функция, позволяющая по величине одного предыдущего признака определить средние величины другого признака.

; .

tga=A

tgb=C

Числовое значение коэффициента А линейной регрессии Y на X говорит, на сколько изменится среднее значение величины Y при изменении величины X на единицу. Свободный член В равен значению Y при X=0.

О силе корреляционной зависимости можно судить по корреляционному полю. Корреляционное поле представляет собой множество точек с координатами (x_i;y_i).